
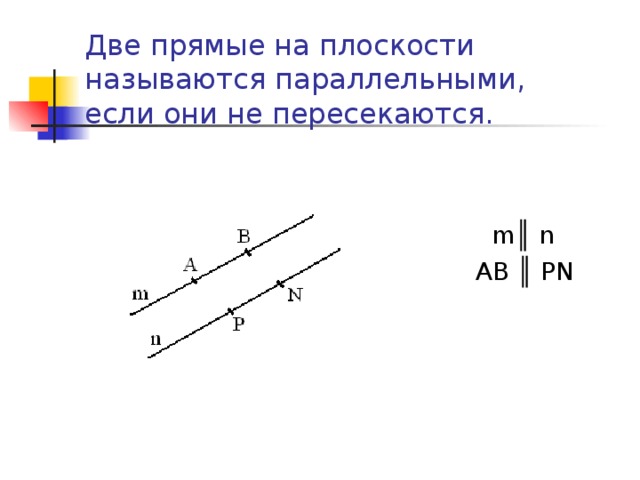
Параллельные прямые в пространстве — это особый случай взаимного расположения прямых. Они никогда не пересекаются и находятся на одной плоскости. Чтобы точно определить, что две прямые являются параллельными, необходимо выполнение двух условий.
Первое условие заключается в том, что прямые должны лежать в одной плоскости. Это означает, что они не могут быть расположены в разных пространственных направлениях. Таким образом, для того чтобы прямые были параллельными, они должны находится в одной плоскости, т.е. не могут быть перпендикулярными и не должны иметь смещения по третьей оси.
Второе условие для параллельности прямых — это их постоянное расстояние друг от друга. Параллельные прямые всегда имеют одинаковое расстояние между собой. Если расстояние между прямыми изменяется, то они уже не могут быть рассматриваться как параллельные.
Таким образом, две прямые в пространстве называются параллельными, если они лежат в одной плоскости и имеют постоянное расстояние друг от друга. Параллельные прямые являются важным понятием в геометрии и находят свое применение в различных областях науки и техники.
Что такое параллельные прямые в пространстве?
Два условия, которые определяют параллельность прямых, включают:
1. Не пересечение
Параллельные прямые никогда не пересекаются, даже если продлены до бесконечности. Поэтому, если две прямые пересекаются в какой-то точке, они не могут быть параллельными.
2. Общая плоскость
Параллельные прямые всегда находятся в одной и той же плоскости. Это означает, что линейки, которые можно положить на обе прямые, без прогибов или вращений, они будут располагаться на одной и той же поверхности.
Параллельные прямые являются важным понятием в геометрии и находят применение во многих областях, включая строительство, физику и математику.
Определение и свойства
Свойства параллельных прямых:
- Они имеют одинаковый угол наклона.
- Расстояние между параллельными прямыми постоянно и одинаково в любой точке.
- Параллельные прямые остаются параллельными при параллельном переносе.
- Они не имеют точек пересечения, но прямые, лежащие в одной прямой плоскости и параллельные третьей прямой, пересекаются.
- Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и всем остальным параллельным прямым.
Аксиомы параллельных прямых
Аксиома 1: Единственность параллельной прямой
Существует только одна прямая, которая параллельна данной и не пересекается с ней.
Аксиома 2: Транзитивность параллельных прямых
Если две прямые параллельны одной третьей прямой, то они параллельны друг другу. Иначе говоря, если прямая А параллельна прямой В, и прямая В параллельна прямой С, то прямая А параллельна прямой С.
Где встречаются параллельные прямые в реальной жизни?
Понятие параллельных прямых находит свое применение в различных областях нашей жизни. Вот некоторые примеры, где встречаются параллельные прямые:
1. Архитектура и строительство
В архитектуре и строительстве параллельные прямые используются для создания симметричных и гармоничных структур. Например, в дизайне зданий параллельные линии могут быть использованы для создания эффекта пространства и перспективы.
2. Дорожное движение
В дорожном движении параллельные прямые используются для обозначения разделительной полосы, маркировки дорожек и парковочных мест. Они помогают водителям ориентироваться на дороге и соблюдать правила безопасности.
Кроме того, параллельные линии могут быть встречены в различных других ситуациях, таких как дизайн интерьера, рисунки и графики, проектирование электрических схем и многое другое. Понимание понятия параллельности помогает нам в анализе и построении различных систем и структур в нашей жизни.
Как определить, являются ли две прямые параллельными?
1. Сравнение коэффициентов наклона
Если две прямые имеют одинаковые коэффициенты наклона, то они параллельны друг другу. Коэффициент наклона обозначается как k и вычисляется по формуле k = (y2 — y1) / (x2 — x1), где (x1, y1) и (x2, y2) — координаты двух точек на прямой.
2. Проверка параллельности с помощью свойства одинаковых углов
Если две прямые пересекаются третьей прямой и образуют одинаковые углы с ней, то они параллельны друг другу.
Важно отметить, что при использовании этих методов необходимо учитывать возможные погрешности измерений и округления значений.
Если отсутствует возможность вычислять коэффициенты наклона или проводить дополнительные измерения, можно также воспользоваться геометрическими методами, такими как построение параллельных прямых с помощью углов или построение параллельных секущих плоскостей.
Как построить параллельную прямую?
Параллельными прямыми называются прямые, которые находятся в плоскости и не пересекаются друг с другом. Для построения параллельной прямой нам понадобятся следующие шаги:
- Выберите произвольную точку на исходной прямой, которую нужно параллельно проложить.
- Постройте перпендикуляр к исходной прямой, проходящий через выбранную точку. Для этого можно воспользоваться циркулем и линейкой или геометрическими построениями.
- Выберите произвольную точку на построенном перпендикуляре.
- Проведите прямую через эту точку и параллельно исходной прямой. Таким образом, новая прямая будет параллельна исходной прямой и проходить через выбранные точки.
Важно учесть, что для построения параллельной прямой необходимо иметь уже построенную исходную прямую. Также обратите внимание на то, что в пространстве можно построить бесконечное количество параллельных прямых к заданной прямой, проходящих через точки вне пересечения с ней.
Зачем нам нужно знать о параллельных прямых?
1. Геометрия и физика
Параллельные прямые играют важную роль в геометрии и физике. Они помогают нам анализировать и понимать свойства фигур и объектов в пространстве. Например, знание параллельных прямых позволяет нам решать задачи на построение перпендикуляров, нахождение углов и расстояний между объектами.
2. Дизайн и архитектура
Знание параллельных прямых является неотъемлемой частью дизайна и архитектуры. Оно помогает дизайнерам и архитекторам создавать эстетически приятные и устойчивые конструкции. Параллельные прямые используются, например, при проектировании зданий, мебели и декоративных элементов.
3. Техническое рисование
Знание параллельных прямых также является важным для технического рисования и черчения. Оно позволяет рисовать точные и симметричные изображения, строить схемы и планы. Например, в инженерном черчении параллельные прямые используются при рисовании эскизов деталей и сборочных единиц.
Итак, знание понятия параллельных прямых является необходимым и полезным для различных областей деятельности, связанных с геометрией и пространством. Это позволяет нам более глубоко понимать окружающий мир и применять геометрию в решении практических задач.
Практические примеры использования параллельных прямых
Параллельные прямые играют важную роль в различных областях, они помогают решать разнообразные задачи и применяются во многих сферах жизни. Рассмотрим несколько практических примеров использования параллельных прямых.
Строительство и архитектура
В строительстве и архитектуре параллельные прямые используются для создания параллельных стен, колонн, балок и других конструкций. Они позволяют обеспечить надежность и прочность зданий, а также равномерное распределение нагрузок.
Например, при строительстве мостов параллельные прямые используются для расчета пролетов и создания определенного расстояния между опорами моста. Это позволяет обеспечить безопасность и устойчивость конструкции.
Геометрия

В геометрии параллельные прямые используются для решения различных задач. Например, они позволяют находить соответствующие углы при пересекающихся прямых для вычисления неизвестных величин. Также параллельные прямые используются для построения и определения размеров фигур, таких как параллелограммы и треугольники.
Кроме того, в проекционной геометрии параллельные прямые используются для создания перспективных изображений и определения точек схода. Это находит применение в архитектуре и искусстве, позволяя создать впечатляющие и реалистичные изображения пространства.
Таким образом, параллельные прямые являются одним из важных инструментов, используемых в различных областях. Они помогают решать задачи конструктивного, математического и художественного характера, обеспечивая точность и надежность в результатах.
Вопрос-ответ:
Как определить, что две прямые в пространстве параллельны?
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Можете ли вы объяснить, как происходит проверка на параллельность прямых в пространстве?
Для проверки параллельности двух прямых в пространстве можно использовать несколько способов. Один из них — проверить, лежат ли прямые в одной плоскости. Для этого нужно проверить, пересекаются ли прямые по какой-либо точке. Если они не пересекаются, то они лежат в одной плоскости и могут быть параллельными. Еще один способ — проверить, что углы между прямыми равны нулю или 180 градусов. Если углы равны нулю, то прямые совпадают и также могут считаться параллельными.
Есть ли какая-то формула или алгоритм, позволяющий определить параллельность прямых в пространстве?
Для определения параллельности двух прямых в пространстве нет какой-то конкретной формулы или алгоритма. Определение параллельности прямых требует анализа их положения в пространстве. Необходимо проверить, что прямые лежат в одной плоскости и не пересекаются. Для этого можно использовать различные методы и приемы геометрии.
Можно ли использовать уравнения прямых для определения их параллельности в пространстве?
Да, можно использовать уравнения прямых для определения их параллельности в пространстве. Для этого можно сравнить коэффициенты при переменных в уравнениях двух прямых. Если коэффициенты при соответствующих переменных совпадают (или пропорциональны), то прямые могут быть параллельными. Однако стоит помнить, что уравнения прямых могут быть записаны в различных формах, и для определения параллельности нужно использовать соответствующие уравнения в нужной форме.