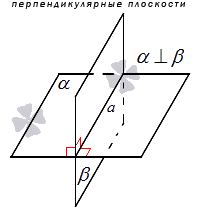
Перпендикулярность — это одно из основных геометрических понятий, которое имеет важное значение в пространстве. В математике перпендикулярные прямые определяются как прямые, которые пересекаются под прямым углом, то есть углом в 90 градусов.
Для понимания перпендикулярности в пространстве необходимо представлять прямые как линии, которые расположены в трехмерном пространстве и простираются в бесконечность. Линия, проходящая через две точки, называется прямой. Если две прямые пересекаются под прямым углом, то они считаются перпендикулярными.
Перпендикулярность может быть проиллюстрирована простым примером: представьте две линии на плоскости, которые пересекаются под прямым углом. Если мы повернем одну из этих линий на 90 градусов в пространстве, то эти линии будут перпендикулярными. Таким образом, перпендикулярность прямых в пространстве возникает, когда они пересекаются под прямым углом и в то же время остаются на одной плоскости.
Понятие перпендикулярности в пространстве широко используется в геометрии, физике, архитектуре и других науках. Оно позволяет определить направления в трехмерном пространстве и применяется при решении различных задач. Понимание перпендикулярности прямых в пространстве помогает улучшить понимание трехмерных объектов и их взаимодействия.
Какие линии считаются перпендикулярными в пространстве
В пространстве существуют две основные геометрические фигуры: прямые линии и плоскости. Перпендикулярные линии могут быть определены в трехмерном пространстве, когда две прямые линии образуют прямой угол. Такие прямые линии пересекаются в точке и не лежат в одной плоскости. Их направления взаимно прямоугольны, и они не пересекаются вне этой точки пересечения.
Примерами перпендикулярных линий в трехмерном пространстве являются:
- Линия, пересекающаяся с плоскостью под прямым углом
- Две прямые линии, пересекающиеся в точке и образующие прямой угол
- Прямая линия, пересекающаяся с плоскостью в точке так, что прямая, проведенная из точки пересечения, образует прямой угол с плоскостью
Перпендикулярные линии широко используются в геометрии и физике, особенно в векторном анализе. Они позволяют определить направление и отношение двух различных линий или пространственных объектов.
Линии, перпендикулярные основным осям
В пространстве существуют различные линии, которые могут быть перпендикулярными к основным осям: X, Y и Z. Перпендикулярность означает, что две линии встречаются под прямым углом, то есть угол между ними равен 90 градусам. Такие линии играют важную роль в геометрии и конструировании.
Линия, перпендикулярная основной оси X, называется осью Y. Она проходит через точку (0, 1, 0) и параллельна плоскости XY. Эта линия пересекает ось X под прямым углом и создает плоскость XY.
Линия, перпендикулярная основной оси Y, называется осью X. Она проходит через точку (1, 0, 0) и параллельна плоскости XZ. Эта линия пересекает ось Y под прямым углом и создает плоскость XZ.
Линия, перпендикулярная основной оси Z, называется осью Z. Она проходит через точку (0, 0, 1) и параллельна плоскости YZ. Эта линия пересекает ось Z под прямым углом и создает плоскость YZ.
Перпендикулярные основным осям линии используются в различных областях, включая архитектуру, инженерное дело, компьютерную графику и другие. Они позволяют строить прямоугольные плоскости и формы, создавать точки отсчета и установить точное положение объектов в пространстве.
Линия, перпендикулярная оси X
Линии, перпендикулярные оси X, располагаются в вертикальной плоскости и не пересекают ось X. В точке пересечения с осью Y создается угол, равный 90 градусов.
Примеры прямых, перпендикулярных оси X:
- Прямая, проходящая через точку (0, 0) и имеющая направление вверх.
- Прямая, проходящая через точку (5, 0) и имеющая направление вниз.
- Прямая, параллельная оси X и находящаяся на постоянном расстоянии от нее.
Перпендикулярные линии в пространстве имеют важное значение в различных областях, включая геометрию, физику, инженерию и архитектуру. Они используются для создания прямых углов, измерения расстояний и построения перпендикулярных линий в проекциях и планах.
Линия, перпендикулярная оси Y
В пространстве существуют различные геометрические объекты, включая линии. Линии могут быть расположены в разных направлениях и иметь разные свойства. Если рассматривать пространство с осями X, Y и Z, где ось Y вертикальна, то перпендикулярная ей линия будет расположена в плоскости, параллельной плоскости XY. Это значит, что данная линия будет пересекать плоскость XY под прямым углом.
Характеристики перпендикулярной линии могут варьироваться в зависимости от конкретного объекта или задачи, в которой она используется. Однако, главное свойство, которое определяет перпендикулярность, это угол 90 градусов между этой линией и осью Y. Именно это свойство позволяет нам определить, что данная линия является перпендикулярной оси Y.
Использование перпендикулярных линий имеет широкий спектр применений в различных отраслях, включая геометрию, архитектуру, инженерное дело и дизайн. Перпендикулярные линии помогают определить направление, уклон или границы объектов, а также создают эстетически приятные и симметричные композиции.
Линия, перпендикулярная оси Z
Ось Z является вертикальной осью, которая направлена вверх или вниз. Линия, перпендикулярная оси Z, будет горизонтальная и плоская. Она будет располагаться в плоскости, перпендикулярной плоскости XY.
| Ось | Направление | Плоскость |
|---|---|---|
| X | Горизонтальное | YZ |
| Y | Вертикальное | XZ |
| Z | Вертикальное | XY |
Линия, перпендикулярная оси Z, может встречаться в разных контекстах. Например, в геометрии она используется для построения плоского прямоугольника или проведения перпендикуляра к плоскости XY.
Также, в физике она может быть использована для определения вектора магнитного поля или проведения измерений в трехмерном пространстве.
Линии, проходящие через центр вписанной окружности и центр описанной сферы
Вписанная окружность – это окружность, которая касается всех сторон многогранника, либо касается всех сторон, кроме одной грани, находящейся на ее плоскости. Центр вписанной окружности совпадает с центром многогранника.
Описанная сфера – это сфера, которая проходит через все вершины многогранника. Центр описанной сферы совпадает с центром многогранника.
Когда рассматриваемые линии проходят через центр вписанной окружности и центр описанной сферы, они образуют прямоугольный угол. Это означает, что угол между такими линиями равен 90 градусам.
Одним из примеров многогранников, в которых такие линии существуют, является куб. В кубе центр вписанной окружности и центр описанной сферы совпадают с центром куба. Линии, проходящие через этот центр и касающиеся граней куба, будут перпендикулярными.
Линии, проходящие через центр вписанной окружности и центр описанной сферы, играют важную роль в геометрии. Они позволяют решать различные задачи и находить взаимосвязи между разными элементами пространства.
Линия, перпендикулярная плоскости, на которой лежит вписанная окружность
В геометрии существует концепция перпендикулярности между прямыми. Две прямые считаются перпендикулярными, если они пересекаются под прямым углом. Однако в трехмерном пространстве понятие перпендикулярности несколько усложняется.
Если рассматривать планарные фигуры, то перпендикулярность прямых легко определить. Но что делать, если в проекции на плоскость мы видим только окружность, но не видим саму прямую, которая лежит в другой плоскости и перпендикулярна этой окружности?
В таком случае можно воспользоваться определенной характеристикой окружности, а именно наличием вписанной окружности. Вписанная окружность — это окружность, которая касается всех сторон фигуры. Она всегда описывается внутри фигуры, независимо от ее формы.
На плоскости, на которой лежит вписанная окружность, можно провести линию, которая будет перпендикулярна этой плоскости. Для этого можно взять две точки на окружности и провести через них прямую. Такая линия будет перпендикулярна плоскости, на которой лежит вписанная окружность, и полностью определена этой окружностью.
Таким образом, в геометрических конструкциях, где присутствует вписанная окружность, можно определить линию, перпендикулярную плоскости, на которой она лежит. Это позволяет решать различные геометрические задачи, связанные с такими конструкциями.
Линия, перпендикулярная плоскости, на которой лежит описанная сфера
В геометрии, существует специальное отношение между прямыми и плоскостями, которое называется перпендикулярностью. Прямая считается перпендикулярной к плоскости, если она пересекает эту плоскость под прямым углом, то есть угол между прямой и плоскостью равен 90 градусов.
Представим, что у нас есть плоскость, на которой лежит описанная сфера. Эта плоскость может быть задана с помощью уравнения вида Ax + By + Cz + D = 0, где A, B, C и D — коэффициенты плоскости.
Чтобы найти линию, перпендикулярную этой плоскости, мы можем воспользоваться следующей формулой: линия, параллельная плоскости, заданной уравнением Ax + By + Cz + D = 0, имеет уравнение Ax + By + Cz + k = 0, где k — некоторая константа.
Для того, чтобы эта линия была перпендикулярна к плоскости, мы можем взять вектор нормали к плоскости, который определяется коэффициентами A, B и C, и направить этот вектор по линии. Таким образом, уравнение линии будет иметь вид Ax + By + Cz + k = 0, где k = A*x + B*y + C*z, где (x, y, z) — координаты точки на линии.
Итак, мы нашли линию, перпендикулярную плоскости, на которой лежит описанная сфера. Теперь мы можем использовать это знание для решения различных задач в геометрии, например, для нахождения точек пересечения линии и плоскости или для определения направления движения линии в пространстве.
Линии, образующие прямые углы с плоскостями
Одной из таких линий является прямая, перпендикулярная плоскости. Перпендикулярность позволяет строить прямоугольные треугольники и прямоугольные параллелепипеды, а также определить расстояние от точки до плоскости.
Другим примером линии, образующей прямой угол с плоскостью, является нормаль к плоскости. Нормаль – это перпендикуляр, проведенный из точки на плоскости к плоскости. Нормаль определяет направление искривления поверхности и позволяет вычислять градиент поля, величину вектора скорости или силы, а также определить угол между плоскостью и направлением.
Для обнаружения перпендикулярных линий и нормалей в пространстве используются различные методы. Например, руководство может обозначить перпендикулярность плоскостей, когда они встречаются друг на друга. Также можно использовать специальные инструменты, например, нивелир, угломер или лазерный нивелир, для измерения и определения перпендикулярности.
| Примеры прямых, перпендикулярных плоскостям | Примеры нормалей к плоскостям |
|---|---|
| Вертикальные линии, проходящие через горизонтальные плоскости | Прямые, перпендикулярные горизонтальным плоскостям |
| Горизонтальные линии, проходящие через вертикальные плоскости | Прямые, перпендикулярные вертикальным плоскостям |
| Диагональные линии, проходящие через плоскости под углом | Прямые, перпендикулярные плоскостям под углом |
Линии, образующие прямые углы с плоскостями, играют важную роль в пространственной геометрии и могут быть использованы для построения и расчета различных конструкций. Их свойства и характеристики позволяют упрощать вычисления и создавать более эффективные дизайны.
Вопрос-ответ:
Что такое перпендикуляр?
Перпендикуляр — это определенное положение двух прямых, при котором они образуют прямой угол друг с другом. Такие прямые пересекаются и не лежат в одной плоскости.
Как определить, являются ли две прямые перпендикулярными в пространстве?
Для определения перпендикулярности двух прямых в пространстве необходимо найти их направляющие векторы и проверить, являются ли эти векторы ортогональными друг другу. Если векторы перпендикулярны, то прямые также будут перпендикулярными.
Какие условия должны выполняться для того, чтобы две прямые были перпендикулярными в пространстве?
Для того, чтобы две прямые были перпендикулярными в пространстве, необходимо выполнение двух условий: первое — прямые должны пересекаться, второе — они не должны лежать в одной плоскости.
Как найти уравнение плоскости, в которой лежит перпендикуляр к двум данным прямым в пространстве?
Для того чтобы найти уравнение плоскости, в которой лежит перпендикуляр к двум данным прямым в пространстве, необходимо воспользоваться методом векторного произведения. Сначала найдем векторное произведение направляющих векторов данных прямых, затем найденный вектор подставим в уравнение плоскости, в результате получим искомое уравнение.