Перпендикулярные векторы — это векторы, которые образуют прямой угол между собой. Если векторы перекрещиваются под углом 90 градусов, то они являются перпендикулярными. Такие векторы рассматриваются в различных областях науки, включая геометрию, физику и инженерию.
Векторы в трехмерном пространстве могут быть перпендикулярными, если их скалярное произведение равно 0. То есть, если сумма произведений соответствующих компонент векторов равна нулю, то это означает, что векторы перпендикулярны. Другими словами, если векторы A и B заданы координатами (x1, y1, z1) и (x2, y2, z2) соответственно, то скалярное произведение выражается следующим образом: A·B = x1*x2 + y1*y2 + z1*z2 = 0.
Перпендикулярные векторы играют важную роль в различных приложениях. Например, векторное произведение двух перпендикулярных векторов используется для определения нормали к плоскости. Также перпендикулярные векторы позволяют описывать направление двух разных физических величин, таких как сила и момент.
Определение перпендикулярных векторов
Два вектора называются перпендикулярными, если они образуют прямой угол (90 градусов) между собой. Это означает, что их скалярное произведение равно нулю.
Скалярное произведение векторов определяется как произведение их длин, умноженное на косинус угла между ними:
Скалярное произведение:
𝑎⋅𝑏 = |𝑎|⋅|𝑏|⋅cos(𝜃)
где 𝑎 и 𝑏 — два вектора, |𝑎| и |𝑏| — их длины, а 𝜃 — угол между ними.
Если скалярное произведение векторов равно нулю, то это означает, что косинус угла между ними равен нулю, а значит, угол между векторами равен 90 градусам.
Например, векторы а(1, 0) и b(0, 1) являются перпендикулярными, так как их скалярное произведение равно 0:
𝑎⋅𝑏 = 1⋅0 + 0⋅1 = 0
Это значит, что вектор a и вектор b образуют прямой угол между собой.
Свойство перпендикулярных векторов
1. Величина скалярного произведения равна нулю
Перпендикулярные векторы обладают свойством, что скалярное произведение между ними равно нулю. Скалярное произведение векторов определяется как произведение их модулей на косинус угла между ними.
2. Угол между перпендикулярными векторами равен 90 градусам
Перпендикулярные векторы образуют прямой угол друг с другом. Угол между векторами можно найти с помощью формулы: косинус угла равен нулю, следовательно, угол равен 90 градусам. Это свойство позволяет использовать перпендикулярные векторы в геометрии и физике, например, для определения направления векторов или для решения задач, связанных с расчетами давления, скорости и силы.
Скалярное произведение векторов
a · b = a₁ * b₁ + a₂ * b₂ + … + aₙ * bₙ
Скалярное произведение является скалярной величиной, то есть числом, а не вектором. Оно имеет несколько интересных свойств и применений:
1. Определение угла
Скалярное произведение векторов позволяет определить угол между ними. Если угол между векторами а и b равен θ, то:
cos(θ) = (a · b) / (|a| * |b|), где |a| и |b| — длины векторов а и b соответственно.
Используя эту формулу, можно вычислить угол между векторами, а также определить, являются ли они перпендикулярными. Если скалярное произведение равно нулю, то векторы перпендикулярны.
2. Проекция вектора
Скалярное произведение также может быть использовано для расчета проекции одного вектора на другой. Проекция вектора a на вектор b может быть вычислена следующим образом:
projba = ((a · b) / |b|²) * b
Это позволяет разложить вектор a на две компоненты: параллельную вектору b и перпендикулярную ему.
Скалярное произведение векторов имеет широкое применение в различных областях математики и физики, таких как геометрия, механика и теория вероятностей. Оно является основой для дальнейших изучений векторов и их свойств.
Критерий перпендикулярности векторов
Перпендикулярными называются два вектора, если их скалярное произведение равно нулю. Скалярное произведение двух векторов определяется как произведение модулей этих векторов на косинус угла между ними.
То есть, если у нас есть два вектора A и B в трехмерном пространстве, то они будут перпендикулярными, если выполняется условие:
A ⋅ B = |A| ⋅ |B| ⋅ cos(α) = 0
где |A| и |B| — это модули векторов A и B соответственно, а cos(α) — косинус угла между ними.
Такой критерий перпендикулярности векторов позволяет определить, являются ли они взаимно ортогональными. Знание этого критерия полезно при решении множества задач и применяется во многих областях науки, инженерии и физике.
Условие перпендикулярности векторов
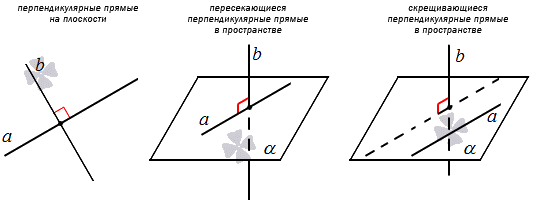
Два вектора называются перпендикулярными, если их скалярное произведение равно нулю. Скалярное произведение двух векторов определяется как произведение модулей этих векторов на косинус угла между ними.
Математически это условие записывается следующим образом:
Вектор A = (A1, A2, A3)
Вектор B = (B1, B2, B3)
Условие перпендикулярности векторов можно записать в виде:
A1 * B1 + A2 * B2 + A3 * B3 = 0
Если скалярное произведение векторов равно нулю, то это означает, что векторы перпендикулярны и составляют прямой угол между собой.
Геометрическое определение перпендикулярности

Чтобы геометрически определить, являются ли два вектора перпендикулярными, можно использовать несколько способов.
- Первый способ: векторы перпендикулярны, если их скалярное произведение равно нулю. Скалярное произведение двух векторов равно произведению модулей этих векторов на косинус угла между ними. Если косинус угла равен нулю, то скалярное произведение будет нулевым, что говорит о перпендикулярности векторов.
- Второй способ: векторы перпендикулярны, если их координаты удовлетворяют условию ортогональности. Для двух векторов, заданных в виде (x1, y1, z1) и (x2, y2, z2), эти векторы будут перпендикулярными, если x1*x2 + y1*y2 + z1*z2 = 0.
- Третий способ: векторы перпендикулярны, если их направляющие числа пропорциональны. Направляющие числа вектора — это его координаты, поделенные на коэффициент перед вектором. Если коэффициенты равны, то векторы перпендикулярны.
Эти способы позволяют с геометрической точки зрения определить перпендикулярность двух векторов и решить задачи, связанные с такими векторами.
Примеры перпендикулярных векторов
Вот несколько примеров перпендикулярных векторов:
- Вектор AB(2, 0) и вектор CD(0, -2) являются перпендикулярными векторами, так как их координаты обратно пропорциональны и образуют прямой угол.
- Вектор XY(3, 4) и вектор PQ(-4, 3) — также перпендикулярные векторы. Они имеют разные значения координат, но их скалярное произведение равно нулю, что говорит о том, что они перпендикулярны.
- Если взять векторы в трехмерном пространстве, например, вектор MN(1, -2, 3) и вектор UV(3, 2, 1), то они также будут перпендикулярными, так как их скалярное произведение равно нулю.
Перпендикулярные векторы имеют важное значение в различных областях, таких как геометрия, физика и информатика. Они помогают в решении различных задач, например, определении прямых и плоскостей, нахождении нормали к поверхности и многих других.
Перпендикулярность с использованием координат
Два вектора называются перпендикулярными, если их скалярное произведение равно нулю. Мы можем использовать координаты векторов для проверки их перпендикулярности. Давайте рассмотрим два вектора: A = (x1, y1, z1) и B = (x2, y2, z2).
Шаг 1: Находим скалярное произведение
Скалярное произведение векторов A и B можно найти по формуле:
A · B = x1*x2 + y1*y2 + z1*z2
Шаг 2: Проверяем условие перпендикулярности
Если скалярное произведение равно нулю, то векторы A и B перпендикулярны. Иначе, они не являются перпендикулярными.
Векторы A и B могут быть представлены в виде координатных столбцов:
A = [x1, y1, z1]
B = [x2, y2, z2]
Также можно использовать геометрический подход для проверки перпендикулярности векторов с использованием координат. Для этого необходимо построить векторы на координатной плоскости и проверить, будут ли они перпендикулярными либо практически перпендикулярными по их графическому изображению.
Важно понимать, что перпендикулярность векторов зависит от их направления и длины. Векторы могут быть параллельными, а не перпендикулярными, если их направления совпадают, или коллинеарными, если они находятся на одной прямой. Однако, если у векторов разные направления и их скалярное произведение равно нулю, то они гарантированно перпендикулярны.
Перпендикулярность в трехмерном пространстве
В трехмерном пространстве векторы называются перпендикулярными, если они образуют прямой угол друг с другом. То есть, угол между двумя перпендикулярными векторами равен 90 градусам.
Чтобы определить, являются ли два вектора перпендикулярными, необходимо проанализировать их координаты. Если скалярное произведение векторов равно нулю, то они перпендикулярны друг другу. Скалярное произведение двух векторов можно найти, умножив соответствующие координаты векторов и сложив полученные произведения.
Перпендикулярные векторы часто используются в геометрии и физике. Например, направление силы может быть перпендикулярным к поверхности, по которой она действует. Также, перпендикулярные векторы могут использоваться для описания плоскостей и трехмерных пространственных форм.
Вопрос-ответ:
Что такое перпендикулярные вектора?
Перпендикулярные вектора — это два вектора, которые образуют прямой угол друг с другом. Они не лежат в одной плоскости и их скалярное произведение равно нулю.
Как определить, что два вектора являются перпендикулярными?
Два вектора являются перпендикулярными, если их скалярное произведение равно нулю. То есть, если у векторов координаты (a, b) и (c, d), то условие перпендикулярности будет выглядеть как a*c + b*d = 0.
Что случится, если два вектора перпендикулярны?
Если два вектора перпендикулярны, то это означает, что они ортогональны друг другу. Их направления будут перпендикулярны, а угол между ними будет равен 90 градусам. Это свойство перпендикулярных векторов широко используется в геометрии и физике.
Какая геометрическая интерпретация у перпендикулярных векторов?
Геометрически перпендикулярные вектора можно представить, как две прямые линии, которые пересекаются под прямым углом. Если нарисовать эти вектора на координатной плоскости, то они будут выглядеть как две линии, встречающиеся в одной точке и образующие прямой угол.
Какое значение имеет скалярное произведение перпендикулярных векторов?
Скалярное произведение перпендикулярных векторов равно нулю. Это свойство позволяет определить, что два вектора являются перпендикулярными. Математически, скалярное произведение векторов равно 0 означает, что угол между ними равен 90 градусам.