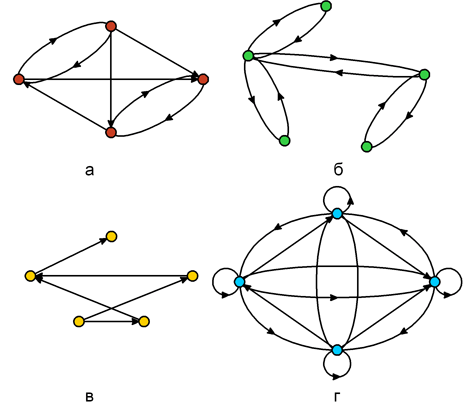
Полный граф — это особый тип графа, в который входят все возможные вершины и все возможные связи между этими вершинами. Другими словами, в полном графе каждая вершина имеет ребра со всеми остальными вершинами. Это делает полный граф чрезвычайно интересным объектом изучения для математиков и компьютерных ученых.
Одна из важных характеристик полного графа — его плотность. Поскольку в полном графе каждая вершина имеет ребра со всеми остальными вершинами, плотность такого графа будет максимальной. Более того, полный граф является полным (полностью связанным), что означает, что он обладает наибольшим числом возможных ребер.
Полные графы широко используются в различных областях, таких как теория графов, социальные сети, маршрутизация пакетов в компьютерных сетях, генетика и т. д. Изучение полных графов позволяет исследовать свойства и характеристики графов в целом, а также разрабатывать и оптимизировать алгоритмы для работы с ними.
Определение полного графа
Для полного графа N вершин образуют полный подграф, в котором есть все N вершин. Полный граф является простым графом без петель и кратных ребер.
Полный граф обозначается символом «K» с индексом, равным количеству вершин, например, Kn.
Полный граф обладает следующим свойством: диаметр полного графа равен 1, а его радиус также равен 1. Это означает, что любые две вершины графа соединены ребром, а кратчайший путь между любыми двумя вершинами состоит из одного ребра.
Достаточное условие полноты графа
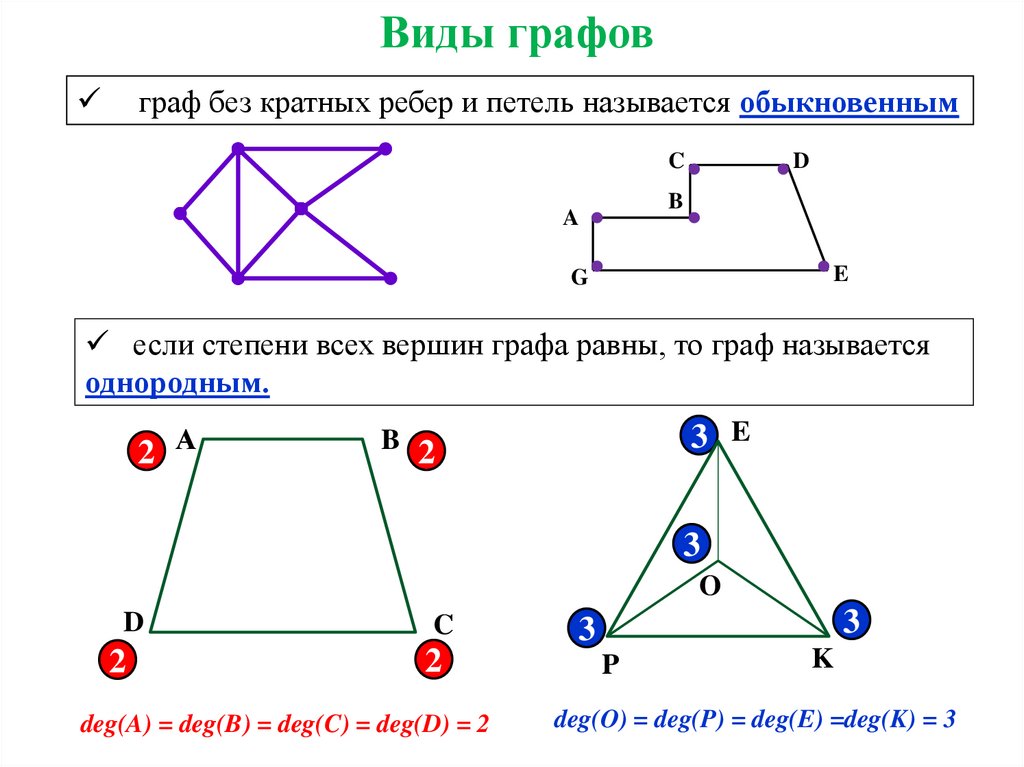
Граф называется полным, если каждая вершина этого графа соединена со всеми другими вершинами. Другими словами, в полном графе каждая пара вершин имеет ребро.
Для определения полноты графа можно использовать достаточное условие. Если в графе с n вершинами количество ребер равно n*(n-1)/2, то граф является полным.
| Количество вершин (n) | Количество ребер (n*(n-1)/2) |
|---|---|
| 2 | 1 |
| 3 | 3 |
| 4 | 6 |
| 5 | 10 |
Например, для графа с 5 вершинами, для того чтобы он был полным, должно быть 10 ребер. Если количество ребер меньше, граф не является полным.
Специальные полные графы
В математике существует несколько видов специальных полных графов, которые обладают определенными уникальными свойствами. Рассмотрим некоторые из них:
1. Полный двудольный граф
Полный двудольный граф — граф, в котором вершины можно разделить на две доли таким образом, что каждая вершина одной доли связана со всеми вершинами другой доли. Такой граф обычно обозначается как Km,n, где m и n — количество вершин в каждой из долей. Полный двудольный граф является важным объектом изучения в теории графов и имеет множество применений в различных областях, включая теорию кодирования и социальные сети.
2. Полный взвешенный граф
Полный взвешенный граф — граф, в котором каждому ребру приписана некоторая числовая величина, называемая весом. В этом графе каждая пара вершин соединена ребром с заданным весом. Полный взвешенный граф обычно используется в задачах оптимизации и алгоритмах поиска кратчайших путей.
3. Полный граф с метриками
Полный граф с метриками — граф, в котором каждой паре вершин приписано некоторое расстояние или метрика. Этот вид графа часто используется в задачах оптимального планирования маршрутов и транспортной логистике. В таком графе каждое ребро имеет свою стоимость, что позволяет находить оптимальные маршруты или рассчитывать стоимость перевозки между вершинами.
Изучение и анализ специальных полных графов позволяет получить глубокое понимание их свойств и использовать их в различных практических задачах.
Степень вершин полного графа
Степень вершины в графе — это количество ребер, исходящих из данной вершины. В полном графе степень каждой вершины равна (n-1).
Понятие степени вершин полного графа имеет важное значение для анализа таких графов. Например, это позволяет определить самую «популярную» вершину (с наибольшей степенью) или находить вершины с определенной степенью. Кроме того, знание степени вершин полного графа упрощает вычисление различных характеристик графа, таких как диаметр, радиус или центральность вершин.
Связность полного графа
Связность графа — это свойство графа, которое определяет, насколько тесно связаны вершины внутри него. Связность графа можно оценить по наличию путей между его вершинами.
Радиус полного графа
Радиус полного графа равен нулю, так как все его вершины находятся на одинаковом расстоянии друг от друга.
Диаметр полного графа
Диаметр полного графа равен единице, так как наименьшее число ребер, которое нужно перейти, чтобы добраться от одной вершины к другой, равно единице. Это объясняется тем, что в полном графе любые две вершины соединены прямым ребром.
Следовательно, полный граф имеет высокую связность, так как любые две его вершины можно соединить путем из одного ребра.
Полные двудольные графы
В полном двудольном графе количество ребер равно произведению количества вершин в каждой доле. Например, если в первой доле графа есть m вершин, а во второй доле – n вершин, то количество ребер равно m * n.
Полные двудольные графы широко применяются в различных областях, например, в теории графов и комбинаторике. Они также находят свое применение в задачах, связанных с распределением ресурсов или планированием.
Данная структура графа может быть использована, например, для моделирования отношений между двумя непересекающимися группами объектов или субъектов.
Полные двудольные графы представляют собой интересный объект изучения, который имеет свои особенности и может быть использован в различных практических задачах.
Полный граф как подграф
Полный граф может также рассматриваться как подграф более общего графа. Полный граф может быть подграфом любого графа G, если каждая его вершина принадлежит G, и между любой парой вершин существует ребро.
Примеры
Полный граф K3 является подграфом полного графа K5. В K3 каждая из трех вершин соединена ребром со всеми остальными двумя вершинами. В K5 также есть связи между всеми пятью вершинами.
Аналогично, полный граф Kn будет подграфом полного графа Km, если n ≤ m.
Использование полных графов в практике
1. Транспортное планирование
Полные графы находят применение в транспортном планировании. Они могут быть использованы для моделирования дорожной сети, планирования маршрутов доставки и оптимизации распределения грузов по различным точкам. Полные графы позволяют учесть все возможные маршруты и найти оптимальный путь доставки.
2. Телекоммуникации
В области телекоммуникаций полные графы используются для моделирования сетевой инфраструктуры, планирования маршрутизации и оптимизации передачи данных. Они позволяют учесть все возможные связи между узлами сети и найти оптимальные пути для передачи информации.
В качестве примера использования полных графов в телекоммуникациях можно привести моделирование мобильной сети, где каждый узел представляет мобильный телефон или базовую станцию, а каждое ребро представляет наличие или отсутствие связи между узлами.
3. Социальные сети
Полные графы также могут быть использованы для анализа социальных сетей. Они позволяют моделировать связи между людьми или другими объектами и анализировать степень взаимодействия и влияние между ними.
Например, в полном графе каждый узел может представлять отдельного человека, а каждое ребро может представлять наличие или отсутствие связи (дружбы) между двумя людьми.
Таким образом, полные графы являются важным инструментом для моделирования и анализа различных ситуаций в практических областях, где важно учесть все возможные связи и найти оптимальные решения.
Вопрос-ответ:
Что такое полный граф?
Полный граф — это граф, в котором каждая вершина связана со всеми остальными вершинами.
Какие другие названия есть у полного графа?
Полный граф также называется полным кликом или полным сочетанием.
Сколько ребер в полном графе с n вершинами?
В полном графе с n вершинами количество ребер равно n*(n-1)/2.
Зачем нужны полные графы?
Полные графы используются в различных областях, например, в теории графов, алгоритмах, коммуникационных сетях и др. Они являются базовым объектом для изучения свойств графов.
Как можно представить полный граф в виде матрицы?
Полный граф с n вершинами можно представить в виде матрицы смежности размером n*n, где каждый элемент равен 1, если соответствующие вершины связаны, и 0 в противном случае.
Что такое полный граф?
Полный граф — это граф, в котором каждая вершина соединена с каждой другой вершиной.
Какое количество ребер есть в полном графе со 100 вершинами?
В полном графе количество ребер равно n(n-1)/2, где n — количество вершин. В данном случае, n = 100, поэтому количество ребер будет равно 100*99/2 = 4950.