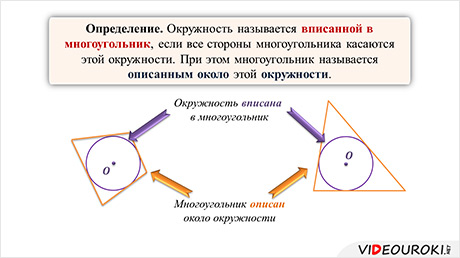
Описанной около четырехугольника называют окружность, которая проходит через все вершины этого четырехугольника. Такая окружность имеет особое свойство: каждая ее хорда, являющаяся диаметром окружности, делит четырехугольник на пару противоположных по сторонам треугольников.
Для определения описанной около четырехугольника окружности необходимо найти центр окружности. Центр описанной около четырехугольника окружности лежит на пересечении перпендикуляров к серединам диагоналей четырехугольника.
Описанная около четырехугольника окружность имеет множество применений в геометрии. Она используется для определения и построения различных геометрических фигур, а также для решения задач с использованием свойств четырехугольника. Понимание понятия описанной около четырехугольника окружности является важным для изучения геометрии и решения геометрических задач.
Определение описанной окружности
Описанной окружностью четырехугольника называется окружность, которая проходит через все вершины данного четырехугольника. Другими словами, окружность описанная вокруг четырехугольника содержит все его вершины на своей границе.
Описанная окружность является важным элементом геометрии. Ее свойства и характеристики позволяют решать различные задачи, связанные с четырехугольниками. Например, с помощью описанной окружности можно определить центр четырехугольника или вычислить его площадь.
Для построения описанной окружности необходимо знать координаты вершин четырехугольника. Существуют различные алгоритмы и методы, которые позволяют найти центр и радиус описанной окружности по координатам вершин четырехугольника.
Описанная окружность имеет ряд свойств. Например, она перпендикулярна диагоналям четырехугольника, а также касается его сторон в точках, которые являются серединами этих сторон. Описанная окружность также является центром вписанной окружности треугольника, образованного диагоналями четырехугольника.
Описанная окружность в геометрии
Для построения описанной окружности необходимо найти центр окружности и радиус. Центр окружности лежит на перпендикулярных биссектрисах двух противоположных углов четырехугольника или в центре окружности, описанной вокруг треугольника, если речь идет о многоугольнике. Радиусом описанной окружности является расстояние от центра до любой вершины четырехугольника или многоугольника.
Описанная окружность является важным объектом в геометрии, так как имеет ряд свойств и связей с другими элементами фигуры. Например, диаметр описанной окружности является диагональю прямоугольника, проведенной между его диагоналями.
Описанная окружность встречается в различных задачах геометрии, таких как нахождение площади четырехугольника, определение вида треугольника (остроугольный, тупоугольный или прямоугольный) и других. Также описанную окружность можно использовать для построения других геометрических фигур и видов окружностей, таких как вписанная окружность или окружность, описанная вокруг правильного многоугольника.
Опеределение описанной окружности в четырехугольниках
Для конструкции описанной окружности в четырехугольнике существует несколько способов. Один из самых распространенных методов основан на использовании диагоналей четырехугольника и их пересечении.
Для построения описанной окружности можно выполнить следующие шаги:
- Найти середины диагоналей четырехугольника.
- Провести прямую, проходящую через найденные середины.
- Найти точку пересечения этой прямой с прямой, соединяющей точки пересечения противоположных сторон четырехугольника. Эта точка будет центром описанной окружности.
- Провести окружность с найденным центром и радиусом, равным расстоянию от центра до любой вершины четырехугольника.
| Рисунок | Описание |
|---|---|
 | Рисунок, иллюстрирующий построение описанной окружности для четырехугольника |
Построение описанной окружности позволяет получить важные характеристики четырехугольника, такие как радиус, диаметр и площадь. Описанная окружность также может быть использована для решения различных геометрических задач, связанных с четырехугольниками.
Важно отметить, что не для всех четырехугольников возможно построить описанную окружность. Выпуклость четырехугольника является необходимым условием для существования описанной окружности.
Способы построения описанной окружности
1. Метод прямоугольников
Один из способов построения описанной окружности четырехугольника — это метод прямоугольников. Для этого необходимо построить два прямоугольника, имеющих общую сторону, являющуюся диагональю описанной окружности. Затем, проведя их общую диагональ косвенно, можно найти центр описанной окружности.
2. Метод пересечения диагоналей
Другой способ построения описанной окружности основан на пересечении диагоналей четырехугольника. Для этого нужно найти точку пересечения диагоналей и от нее отложить радиус окружности до вершин четырехугольника. Полученные точки будут являться концами диаметра описанной окружности.
Изучение способов построения описанной окружности позволяет лучше понять свойства четырехугольников и использовать их в реальных задачах. Использование геометрических методов построения помогает упростить и ускорить решение различных задач, связанных с четырехугольниками и описанными окружностями.
Процесс построения описанной окружности
Шаг 1: Нахождение центра описанной окружности
Для того чтобы построить описанную окружность, необходимо найти ее центр. Центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам четырехугольника.
Шаг 2: Нахождение радиуса описанной окружности
После определения центра описанной окружности можно найти ее радиус. Радиус описанной окружности равен расстоянию от центра до любой вершины четырехугольника. Это можно сделать с помощью формулы расстояния между двумя точками.
После нахождения радиуса описанной окружности можно построить ее, отметив центр и нарисовав окружность с заданным радиусом.
Графическое построение описанной окружности
Описанная окружность в четырехугольнике – это окружность, которая проходит через все вершины этого четырехугольника. Для построения описанной окружности нам понадобятся следующие шаги:
1. Найти середины сторон
Проведите срединные перпендикуляры к сторонам четырехугольника. Точки пересечения этих перпендикуляров с являются серединами сторон.
2. Построить перпендикуляры от середин сторон к противоположным вершинам
Продлите каждую из серединных перпендикуляров до пересечения с противоположными вершинами. Найдите точки пересечения этих перпендикуляров с вершинами.
3. Найти середины противоположных сторон
Проведите срединные перпендикуляры к противоположным сторонам четырехугольника. Точки пересечения этих перпендикуляров с являются серединами противоположных сторон.
4. Провести диагонали четырехугольника
Постройте диагонали четырехугольника, соединяющие противоположные вершины.
5. Найти точку пересечения диагоналей
Найдите точку пересечения диагоналей четырехугольника. Эта точка является центром описанной окружности.
6. Построить окружность
Определите радиус описанной окружности, который равен расстоянию от центра окружности до любой из вершин четырехугольника. Используя найденный радиус и центр окружности, нарисуйте описанную окружность.
Теперь, основываясь на вышеописанных шагах, вы сможете построить описанную окружность в четырехугольнике.
Свойства описанной окружности
Описанной окружностью называют окружность, которая проходит через все вершины четырехугольника. У неё есть несколько свойств, которые следует учитывать при решении задач, связанных с четырехугольниками:
| Свойство | Описание |
|---|---|
| 1 | Описанная окружность всегда является окружностью вписанной в треугольники, образованные диагоналями четырехугольника. |
| 2 | Центр описанной окружности совпадает с точкой пересечения диагоналей четырехугольника, если такая точка существует. |
| 3 | Радиус описанной окружности равен половине длины одной из диагоналей четырехугольника. |
| 4 | Длины хорд, проведенных на окружности из вершин четырехугольника, удовлетворяют теореме Шнейтера – Берштейна: произведение длин хорд, проведенных из противоположных вершин, равно произведению длин других двух хорд. |
| 5 | Если четырехугольник является выпуклым и стороны не пересекаются, то сумма противолежащих углов, опирающихся на одну и ту же хорду, равна 180 градусов. |
Зависимость свойств описанной окружности от типа четырехугольника
Описанной окружностью называется окружность, которая проходит через все вершины четырехугольника и имеет свойства, зависящие от типа этого четырехугольника.
Если четырехугольник является выпуклым и неромбическим, то его описанная окружность будет иметь следующие свойства:
- Центр окружности будет лежать на пересечении диагоналей четырехугольника.
- Радиус окружности будет равен половине длины диагонали.
- Описанная окружность будет касаться всех сторон четырехугольника.
Если четырехугольник является выпуклым ромбом, то его описанная окружность будет иметь следующие свойства:
- Центр окружности будет совпадать с центром ромба.
- Радиус окружности будет равен длине стороны ромба.
- Описанная окружность будет касаться всех вершин ромба.
В случае невыпуклого или самопересекающегося четырехугольника описанная окружность может иметь различные свойства, такие как:
- Центр окружности может находиться как внутри, так и вне четырехугольника.
- Радиус окружности может быть разным в зависимости от размеров и формы четырехугольника.
- Описанная окружность может пересекать или касаться сторон четырехугольника в разных точках.
Таким образом, свойства описанной окружности зависят от типа четырехугольника и его геометрических характеристик.
Вопрос-ответ:
Что такое описанная около четырехугольника окружность?
Описанной около четырехугольника окружностью называется окружность, которая проходит через все вершины четырехугольника.
Как найти центр описанной около четырехугольника окружности?
Центр описанной около четырехугольника окружности можно найти, проведя перпендикуляры к сторонам четырехугольника из середин этих сторон. Точка пересечения этих перпендикуляров будет центром описанной около четырехугольника окружности.
Как доказать, что окружность является описанной около четырехугольника?
Чтобы доказать, что окружность является описанной около четырехугольника, необходимо проверить, что все вершины четырехугольника лежат на данной окружности. Для этого можно использовать свойство равенства углов между хордами и дугами, либо свойство прямых углов, образуемых диагоналями четырехугольника.
Может ли четырехугольник иметь несколько описанных окружностей?
Нет, четырехугольник может иметь только одну описанную около него окружность. Описанная около четырехугольника окружность определена однозначно по его вершинам.
Какая связь между описанной около четырехугольника окружностью и его углами?
Описанная около четырехугольника окружность связана с его углами следующим образом: если в четырехугольнике два противоположных угла смежны, то они равны и опираются на одну и ту же дугу описанной около него окружности.