Правильный многоугольник — это такой многоугольник, у которого все его стороны и углы равны между собой. Другими словами, это многоугольник, в котором все его грани и углы идентичны. Именно эта особенность делает его особенным и запоминающимся.
Примерами правильных многоугольников могут служить треугольник, четырехугольник, пятиугольник, шестиугольник и так далее. Важно отметить, что правильные многоугольники также имеют определенные свойства, которые можно использовать для их классификации.
Одно из главных свойств правильных многоугольников — это угол. Все углы правильного многоугольника равны между собой и равны 360 градусам, поскольку эта сумма углов является универсальной для всех многоугольников. Это отличает правильные многоугольники от неправильных, у которых углы могут быть различными.
Виды многоугольников: основные понятия и определения
1. Треугольник
Треугольник — это многоугольник, имеющий три стороны и три угла. Он является наименее сложной фигурой среди всех многоугольников.
2. Четырехугольник
Четырехугольник — это многоугольник, имеющий четыре стороны и четыре угла. Среди четырехугольников выделяют квадрат, прямоугольник, ромб, параллелограмм и трапецию.
| Название | Описание |
|---|---|
| Квадрат | Четырехугольник, у которого все стороны равны и все углы прямые. |
| Прямоугольник | Четырехугольник, у которого все углы прямые, но не все стороны равны. |
| Ромб | Четырехугольник, у которого все стороны равны, но не все углы прямые. |
| Параллелограмм | Четырехугольник, у которого противоположные стороны параллельны. |
| Трапеция | Четырехугольник, у которого две стороны параллельны, а две другие — нет. |
Это только некоторые из четырехугольников, других видов четырехугольников существует намного больше.
Кроме треугольника и четырехугольника, есть также многоугольники с более чем четырьмя сторонами. Однако основные понятия и определения связанные с ними можно рассмотреть отдельно.
Основные понятия: многоугольник и его свойства
Многоугольник может быть выпуклым или невыпуклым. Если все углы многоугольника меньше 180 градусов, то он называется выпуклым. Если же есть хотя бы один угол многоугольника, который больше 180 градусов, то такой многоугольник называется невыпуклым.
В зависимости от длин сторон и углов, многоугольник может быть правильным или неправильным. Правильный многоугольник — это многоугольник, у которого все стороны равны между собой, а все углы равны. Неправильный многоугольник — это многоугольник, у которого длины сторон и/или углы не равны между собой.
Например:
Треугольник с тремя равными сторонами и тремя равными углами является правильным треугольником.
Четырехугольник со всеми углами равными и двумя парами равных сторон является правильным четырехугольником.
Правильные и неправильные многоугольники: что это такое?
Существует несколько разновидностей правильных многоугольников в зависимости от количества вершин:
- Треугольник – правильный многоугольник с тремя вершинами, трёхугольник имеет три стороны и три угла.
- Квадрат – правильный многоугольник с четырьмя вершинами, квадрат имеет четыре стороны и четыре угла.
- Пятиугольник – правильный многоугольник с пятью вершинами, пятиугольник имеет пять сторон и пять углов.
Неправильные многоугольники – это многоугольники, у которых не все стороны равны и не все углы равны. Их стороны и углы могут иметь разные значения. Если многоугольник не является правильным, то он называется неправильным многоугольником.
Правильные многоугольники являются основой для изучения геометрии и имеют много применений в различных областях науки и практического применения.
Что такое правильный многоугольник? Свойства и определение
Основные свойства правильных многоугольников:
| Количество вершин | У каждого правильного многоугольника количество вершин совпадает с количеством его сторон. |
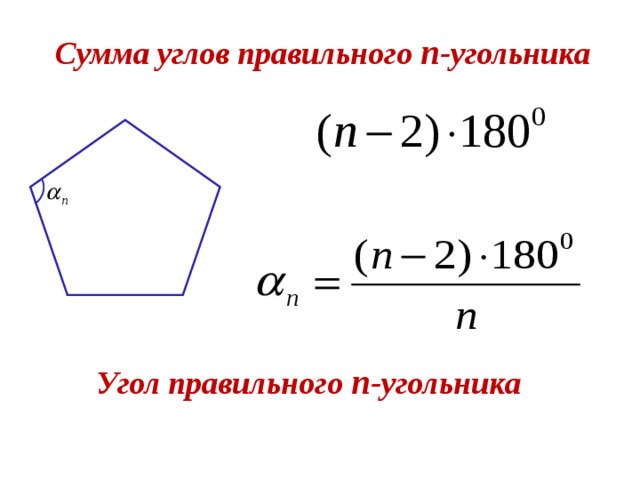
| Сумма углов | Сумма всех углов правильного многоугольника равна (N — 2) * 180 градусов, где N — количество вершин. |
| Угол между сторонами | Угол между любыми двумя сторонами правильного многоугольника равен (N — 2) * 180° / N, где N — количество вершин. |
| Периметр | Периметр правильного многоугольника можно вычислить, умножив длину одной стороны на количество сторон. |
| Площадь | Площадь правильного многоугольника можно вычислить, разделив его на равносторонние треугольники и используя формулу для площади треугольника. |
Изучение свойств и определение правильных многоугольников являются важными в математике и имеют широкое применение в геометрии и других областях науки и техники.
Основные виды правильных многоугольников
Правильными многоугольниками называются многоугольники, у которых все стороны равны между собой и все углы равны. Они обладают особыми свойствами и встречаются в различных областях науки и техники.
Наиболее известными видами правильных многоугольников являются:
| Имя | Количество сторон (n) | Сумма внутренних углов (ε) | Формула для нахождения площади (A) |
|---|---|---|---|
| Треугольник | 3 | 180° | A = (a * h) / 2 |
| Квадрат | 4 | 360° | A = a^2 |
| Пятиугольник | 5 | 540° | A = (a^2 * n) / 4 * tan(π/n) |
| Шестиугольник | 6 | 720° | A = (3 * a^2 * sqrt(3)) / 2 |
| Восьмиугольник | 8 | 1080° | A = 2 * a^2 * (1 + sqrt(2)) |
Это лишь некоторые из многочисленных правильных многоугольников, которые имеют свои названия и характеристики. Правильные многоугольники являются геометрическими фигурами с симметричной структурой и находят применение в различных областях, таких как строительство, кристаллография, компьютерная графика и дизайн.
Как вычислить периметр правильного многоугольника?
Периметр правильного многоугольника можно вычислить, зная длину одной из его сторон и количество сторон в многоугольнике.
Для начала нужно понять, что такое правильный многоугольник. Правильный многоугольник — это многоугольник, у которого все стороны равны между собой, и все углы равны.
Для вычисления периметра правильного многоугольника достаточно умножить длину одной из его сторон на количество сторон. То есть:
Периметр = Длина стороны * Количество сторон
Например, если у нас есть правильный треугольник, у которого длина стороны равна 5 см, то его периметр будет:
Периметр = 5 см * 3 = 15 см
Таким образом, мы можем вычислить периметр любого правильного многоугольника, зная длину одной стороны и количество сторон.
Как вычислить площадь правильного многоугольника?
Шаг 1: Разбиение правильного многоугольника на треугольники
Первый шаг заключается в разбиении правильного многоугольника на несколько треугольников, у которых одна из сторон совпадает с одной из сторон многоугольника, а вершина одного из углов лежит в его центре. Чем больше треугольников возьмется для разбиения, тем более точным будет полученный результат.
Шаг 2: Вычисление площади треугольника
После разбиения правильного многоугольника на треугольники, необходимо вычислить площадь каждого треугольника. Для этого можно использовать формулу площади треугольника, которая зависит от длины его сторон или длины стороны и значение угла между ними.
Шаг 3: Суммирование площадей треугольников
После вычисления площади каждого треугольника, полученные значения следует сложить, чтобы получить площадь всего правильного многоугольника.
Вычисление площади правильного многоугольника может быть сложным процессом, особенно при большом количестве сторон. Однако, с использованием формулы площади треугольника и разбиения многоугольника на треугольники, это вычисление может быть упрощено и уточнено.
| Шаг | Описание |
|---|---|
| Шаг 1 | Разбить правильный многоугольник на треугольники |
| Шаг 2 | Вычислить площадь каждого треугольника |
| Шаг 3 | Сложить площади треугольников |
Полигон и многоугольник: что это такое и в чем разница?
Полигон
Полигон – это фигура, состоящая из любого числа отрезков, которые могут быть не только прямыми, но и кривыми. Вершины полигона соединены таким образом, что они не пересекаются и образуют замкнутый контур. При этом углы между соседними отрезками произвольны, т.е. могут быть различными.
Многоугольник
Многоугольник – это частный случай полигона, в котором все углы между соседними отрезками равны, а все стороны одинаковой длины. Такой многоугольник называется правильным.
Основная разница между полигоном и многоугольником заключается в том, что многоугольник имеет строгие ограничения на форму и длину сторон, в то время как полигон может быть любой формы и размера.
Для наглядного примера различия между полигоном и многоугольником рассмотрим таблицу ниже:
| Тип фигуры | Описание | Пример |
|---|---|---|
| Полигон | Любая фигура, состоящая из отрезков | Треугольник, прямоугольник, квадрат |
| Многоугольник | Фигура с равными углами и сторонами | Равносторонний треугольник, шестиугольник, восьмиугольник |
Таким образом, полигон – это более общее понятие, которое охватывает все фигуры, состоящие из отрезков, в то время как многоугольник – это частный случай полигона с определенными ограничениями на форму и структуру.
Интересные факты о правильных многоугольниках
1. Правильные многоугольники и золотое сечение
Интересно, что правильные многоугольники связаны с золотым сечением. Например, правильный пятиугольник можно построить с использованием золотого сечения (внутренние отношения его сторон соответствуют золотому числу).
2. Все правильные многоугольники могут быть вписаны в окружность
Второй интересный факт о правильных многоугольниках — все они могут быть вписаны в окружность, то есть все вершины правильного многоугольника лежат на окружности, а стороны касаются окружности.
Правильные многоугольники — это удивительные геометрические фигуры, которые представляют собой идеальное сочетание равных сторон и углов. Изучение их свойств и использование в различных областях науки и искусства делает их еще более интересными и значимыми.
Вопрос-ответ:
Какой многоугольник называют правильным?
Правильным многоугольником называется многоугольник, у которого все стороны и все углы равны.
Как вычислить площадь правильного многоугольника?
Площадь правильного многоугольника можно вычислить с помощью формулы: половина произведения периметра на радиус вписанной окружности.
Как найти радиус вписанной окружности в правильный многоугольник?
Радиус вписанной окружности в правильный многоугольник равен половине длины стороны.
Как найти радиус описанной окружности в правильный многоугольник?
Радиус описанной окружности в правильный многоугольник можно найти по формуле: радиус описанной окружности равен половине диагонали.
Как найти длину стороны правильного многоугольника по его радиусу?
Длина стороны правильного многоугольника можно найти, используя формулу: длина стороны равна удвоенному радиусу, умноженному на синус угла между радиусом и стороной многоугольника.
Что такое правильный многоугольник?
Правильный многоугольник — это многоугольник, у которого все стороны равны и все углы равны.