
Рациональные числа – это семейство чисел, которое включает в себя все числа, которые можно представить в виде отношения двух целых чисел. Они обозначаются символом Q и образуют множество, состоящее из всех десятичных, обыкновенных и целых чисел.
Рациональные числа можно представить в виде десятичной дроби, обыкновенной дроби или в виде целого числа. Например, 1/2, 0.5 и 6 являются рациональными числами, так как они могут быть представлены в виде отношения двух целых чисел.
Рациональные числа имеют очень важное свойство – они обладают конечной или периодической десятичной записью. Это означает, что после определенного количества знаков после запятой, десятичная запись истощается или начинается повторяться.
Примером рационального числа может служить число π. Хотя оно является иррациональным, оно может быть представлено в виде десятичной дроби 3.14159…
Рациональные числа играют важную роль в математике и находят применение в различных областях. Они широко используются в финансовых расчетах, в науке и при решении различных задач, где требуется точность до определенного количества знаков после запятой.
Рациональные числа: что это такое и как их определить
Для определения, является ли число рациональным, нужно проверить, может ли оно быть записано в виде дроби. Если число может быть представлено дробью, то оно рациональное, в противном случае — иррациональное.
Существует несколько способов определить, является ли число рациональным или иррациональным. Один из них — это записать число в десятичной форме и проверить, является ли оно конечным или периодическим. Если десятичное представление числа заканчивается или повторяется, то число рациональное, в противном случае — иррациональное.
Другой способ — это использовать свойство рациональных чисел, которые могут быть записаны в виде сокращенной дроби, то есть такой дроби, где числитель и знаменатель не имеют общих делителей, кроме 1. Если число можно представить в виде сокращенной дроби, то оно рациональное.
Рациональные числа играют важную роль в математике и широко используются в различных областях науки и техники. Изучение и понимание рациональных чисел является основой для более сложных понятий и операций, таких как действительные числа и вычисления с ними.
Что такое рациональные числа и как они определяются
1. Числитель и знаменатель
Числитель и знаменатель рационального числа могут быть любыми целыми числами, за исключением случая, когда знаменатель равен нулю. В этом случае дробь становится недопустимой, так как деление на нуль неопределено.
2. Виды рациональных чисел
Рациональные числа могут быть как положительными, так и отрицательными. В зависимости от знака числителя и знаменателя, дробь может быть положительной или отрицательной.
Например, 1/2, -3/4, 10/1 — все они являются рациональными числами, так как их числители и знаменатели — целые числа.
Рациональные числа могут быть записаны как конечные десятичные дроби (например, 0,5), повторяющиеся десятичные дроби (например, 0,333…) или бесконечные неповторяющиеся десятичные дроби (например, √2).
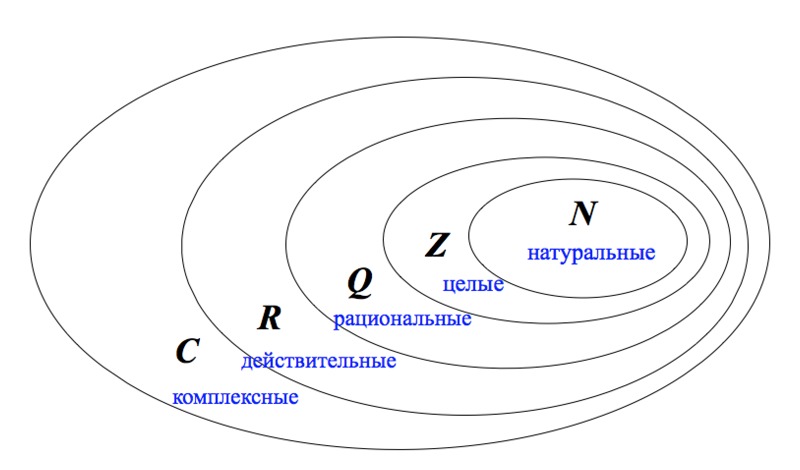
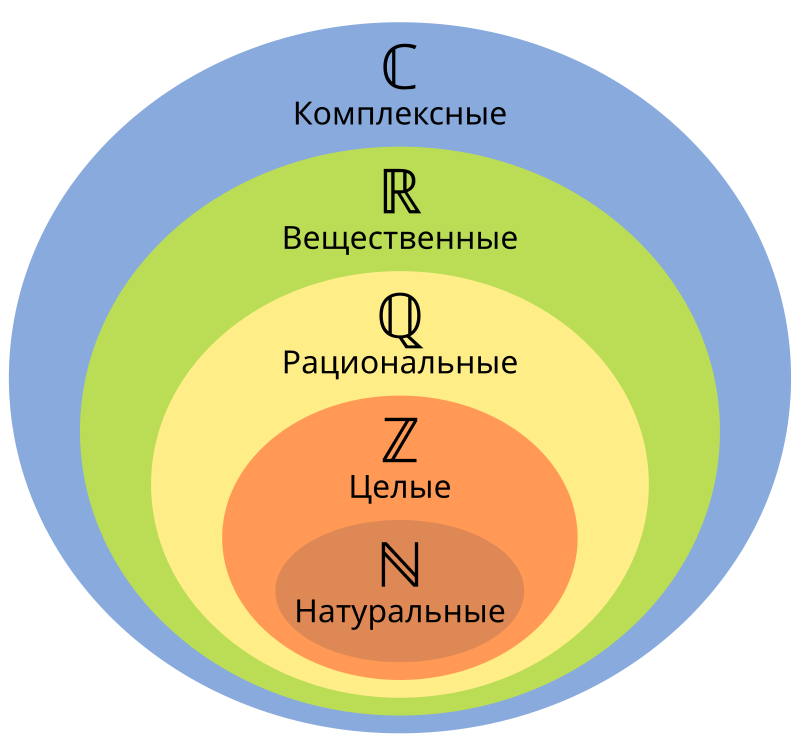
Важно отметить, что рациональные числа образуют множество, которое содержит все целые числа, а также все десятичные числа.
Таким образом, рациональные числа являются важным классом чисел, которые широко используются в математике и других науках для описания различных явлений и вычислений.
Различия между рациональными и иррациональными числами
1. Представление чисел
Рациональные числа могут быть представлены в виде дробей, где числитель и знаменатель являются целыми числами. Например, 1/2, 3/4, 2/5 — это рациональные числа. Они также могут быть представлены в виде десятичных дробей, которые имеют конечное или периодическое представление. Например, 0.5, 0.75, 0.4(6) — это рациональные числа.
Иррациональные числа, с другой стороны, не могут быть представлены в виде дроби и имеют бесконечное и не периодическое десятичное представление. Некоторые примеры иррациональных чисел включают в себя корень из 2 (√2), пи (π), и число е (е).
2. Приближение чисел
Рациональные числа могут быть приближены другими рациональными числами с любой заданной точностью. Например, если мы хотим приблизить число 1/3, мы можем использовать дробь 1/3, 2/6, 3/9 и т. д. Чем больше знаменатель у дроби, тем точнее приближение.
Иррациональные числа, напротив, не могут быть точно приближены рациональными числами. Мы всегда можем приблизить иррациональное число некоторой десятичной дробью, но это будет только приближение, и оно будет иметь ограниченную точность.
3. Арифметические операции
Рациональные числа подчиняются всем правилам арифметики, включая сложение, вычитание, умножение и деление. Если рациональные числа складываются или умножаются, результат будет рациональным числом.
Иррациональные числа, в то же время, имеют свои особенности при арифметических операциях. Например, если мы сложим иррациональное число с рациональным числом, результат будет иррациональным числом. Если мы умножим иррациональное число на рациональное число, результат также будет иррациональным числом.
| Тип числа | Примеры |
|---|---|
| Рациональные числа | 1/2, 0.75, 2/3 |
| Иррациональные числа | √2, π, е |
Примеры рациональных чисел в повседневной жизни
1. Деньги
Цены на товары и услуги в магазинах часто имеют десятичные обозначения, что означает, что они являются рациональными числами. Например, цена 5,99 рубля — это рациональное число, которое можно представить как 599/100.
2. Время
Время также может быть представлено в виде рациональных чисел. Например, 2.5 часа равно 2 часам и 30 минутам, что можно записать как 5/2 часа.
Это лишь некоторые примеры рациональных чисел, которые мы используем в повседневной жизни. Рациональные числа играют важную роль во многих аспектах нашей жизни, и их понимание помогает нам решать различные математические и практические задачи.
Свойства и операции с рациональными числами
Одно из основных свойств рациональных чисел — замкнутость относительно операции сложения и умножения. При сложении или умножении двух рациональных чисел результат также будет рациональным числом.
Следующим важным свойством является существование обратного элемента относительно операции сложения и умножения. Для любого рационального числа a существует рациональное число -a, такое что a + (-a) = 0 и a * (1/a) = 1.
Также рациональные числа удовлетворяют свойствам коммутативности и ассоциативности операций сложения и умножения. Это значит, что порядок чисел не влияет на результат операции, а скобки в выражении можно расставлять произвольным образом.
Другим важным свойством рациональных чисел является существование обратного элемента относительно операции деления. Для любого ненулевого рационального числа a существует рациональное число 1/a, такое что a * (1/a) = 1.
Операции сложения, вычитания, умножения и деления с рациональными числами выполняются так же, как и с целыми числами. Они подчиняются тем же правилам, с которыми мы уже знакомы.
Например, чтобы сложить два рациональных числа, нужно сложить их числители и знаменатели по отдельности. То же самое касается и вычитания рациональных чисел.
Умножение рациональных чисел выполняется путем умножения числителей и знаменателей по отдельности.
Деление рациональных чисел выполняется путем умножения делимого на обратное значение делителя.
Знание свойств и операций с рациональными числами позволяет нам выполнять различные математические операции и решать уравнения, а также применять их в реальной жизни, включая финансовые расчеты, любые виды измерений и т. д.
Как рациональные числа представляются на числовой прямой
Для начала, устанавливаем точку отсчета на числовой прямой, называемую нулем. Затем, выбираем единичный отрезок, который будет представлять единицу. Этот отрезок может быть выбран произвольно, но обычно выбирают отрезок фиксированной длины для удобства. Например, можно выбрать отрезок длиной 1 см или 1 дюйм.
После установки нуля и единицы на числовой прямой, можно начать представлять рациональные числа. Некоторые рациональные числа, такие как целые числа, могут быть представлены простым способом. Например, число 1 будет представлено на числовой прямой путем отметки точки на единичном отрезке от нуля. Для представления отрицательных чисел можно отмечать точки слева от нуля.
Кроме того, для представления дробей, можно использовать разделение единичного отрезка на равные части. Например, чтобы представить число 1/2, можно разделить единичный отрезок на 2 равных части и отметить точку на половине отрезка. Рациональные числа, которые больше или меньше 1, могут быть представлены аналогичным образом.
На числовой прямой рациональные числа будут располагаться в определенном порядке. Числа, которые находятся ближе к нулю, будут меньше рациональных чисел, которые находятся дальше от нуля. Таким образом, с помощью числовой прямой можно увидеть отношения между рациональными числами и их распределение по величине.
В целом, числовая прямая позволяет наглядно представить рациональные числа и их взаимные отношения. Она помогает нам лучше понять структуру и свойства рациональных чисел, что может быть полезным в различных областях математики и ее приложениях.
Рациональные числа и их использование в математике
Рациональные числа играют важную роль в математике и используются в различных областях. Они широко применяются в алгебре, геометрии, физике, экономике и других науках.
Одно из наиболее распространенных применений рациональных чисел – решение уравнений. Благодаря своей простоте и доступности, дроби помогают нам вычислять значения неизвестных в уравнениях и неравенствах.
Рациональные числа также используются для представления и измерения величин в физике и инженерии. Они позволяют нам выражать и сравнивать доли, проценты, коэффициенты и другие величины, которые могут быть представлены в виде дробей.
Более того, рациональные числа используются в геометрии для представления отношений между длинами, площадями и объемами фигур. Они позволяют нам строить отношения между сторонами треугольников, прямоугольниками и другими фигурами.
Отношение рациональных чисел к другим видам чисел
Рациональные числа и целые числа
Все целые числа также являются рациональными числами. Целые числа могут быть представлены в виде дробей с знаменателем, равным единице. Например, число 5 можно записать как 5/1, что является рациональным числом.
Рациональные числа и иррациональные числа
Иррациональные числа являются числами, которые не могут быть представлены в виде дроби. Например, число пи (π) является иррациональным числом. В отличие от рациональных чисел, иррациональные числа имеют бесконечное количество непериодических десятичных разрядов.
Рациональные числа и иррациональные числа вместе составляют множество всех вещественных чисел. Вещественные числа включают в себя как рациональные, так и иррациональные числа.
Все рациональные числа можно отнести к множеству алгебраических чисел, так как они являются решениями алгебраических уравнений с целыми коэффициентами. Однако иррациональные числа не могут быть представлены в виде конечных или периодических алгебраических уравнений и поэтому не являются алгебраическими числами.
Вопрос-ответ:
Что такое рациональное число?
Рациональное число — это число, которое можно представить в виде дроби, где числитель и знаменатель являются целыми числами.
Как определить, что число является рациональным?
Для того чтобы определить, что число является рациональным, необходимо проверить, может ли оно быть представлено в виде дроби с целыми числами в числителе и знаменателе.
Как найти разложение рационального числа в виде десятичной дроби?
Чтобы найти разложение рационального числа в виде десятичной дроби, нужно разделить числитель на знаменатель. Результатом будет конечная или бесконечная десятичная дробь.
Можно ли представить все рациональные числа в виде конечной десятичной дроби?
Нет, не все рациональные числа можно представить в виде конечной десятичной дроби. Некоторые рациональные числа могут иметь бесконечное, но периодическое разложение в десятичной системе.
Как рациональные числа связаны с целыми числами?
Целые числа являются частным случаем рациональных чисел, т.е. все целые числа также являются рациональными числами.
Что такое рациональное число?
Рациональное число — это число, которое может быть представлено в виде дроби, где числитель и знаменатель являются целыми числами. В этом случае знаменатель не может быть равен нулю.
Как узнать, является ли число рациональным?
Чтобы определить, является ли число рациональным, нужно проверить, может ли оно быть представлено в виде дроби. Если число может быть записано в виде дроби, то оно является рациональным. В противном случае, если число не может быть представлено в виде дроби, оно является иррациональным числом.