
В мире геометрии существует множество понятий, которые помогают нам лучше понять структуру и свойства пространства. Одно из таких понятий — расстояние между прямой и параллельной ей плоскостью. Это величина, которая определяет насколько далеко находятся эти два объекта друг от друга. Расстояние может быть положительным или отрицательным в зависимости от направления и положения плоскости относительно прямой.
Для вычисления расстояния между прямой и параллельной ей плоскостью используется специальная формула. Она основана на принципе, что любую точку на плоскости можно представить как сумму двух векторов: один вектор параллелен прямой, а другой — ортогонален ей. Зная координаты точки и направляющего вектора прямой, а также нормального вектора плоскости, можно легко вычислить расстояние между ними.
Расстояние между прямой и параллельной ей плоскостью имеет важное значение во многих областях науки и техники. Оно применяется при решении задач в физике, инженерии, компьютерной графике и других дисциплинах. Адекватное понимание этого понятия помогает разработчикам создавать более точные и эффективные модели систем, а также прогнозировать и анализировать различные физические явления.
Расстояние между прямой и параллельной плоскостью
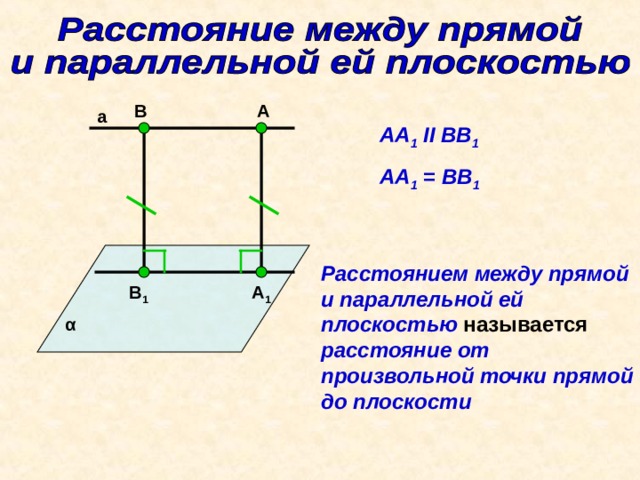
Для того чтобы найти расстояние между прямой и параллельной плоскостью, необходимо знать уравнение прямой и уравнение плоскости. Если известны координаты точки прямой и координаты нормального вектора плоскости, то расстояние можно вычислить по формуле:
Формула расстояния между прямой и параллельной плоскостью:
d = |(Ax0 + By0 + Cz0 + D)| / sqrt(A^2 + B^2 + C^2),
где (x0, y0, z0) — координаты точки прямой, A, B, C — коэффициенты уравнения плоскости (Ax + By + Cz + D = 0).
В случае, если вычисленное расстояние отрицательно, это означает, что точка прямой находится по ту сторону плоскости, куда направлен нормальный вектор.
Определение расстояния
Для определения расстояния между прямой и параллельной ей плоскостью можно использовать различные методы. Один из самых простых методов – это построение перпендикуляра от прямой к плоскости и измерение длины этого перпендикуляра.
Также расстояние можно вычислить, зная уравнения прямой и плоскости, и применив соответствующие формулы. Например, если уравнение прямой задано в параметрической форме, а уравнение плоскости задано в общем виде, то расстояние можно вычислить с помощью формулы, учитывающей координаты точки пересечения прямой и плоскости.
Определение расстояния между прямой и параллельной ей плоскостью играет важную роль в различных областях, таких как геометрия, физика, инженерия и прочие. Это понятие помогает решать задачи, связанные с визуализацией и измерением расстояний в трехмерном пространстве.
Геометрическое представление
Геометрическое представление расстояния между прямой и параллельной ей плоскостью позволяет нам визуализировать это понятие и лучше понять его смысл. Рассмотрим прямую, которая лежит в трехмерном пространстве, и параллельную ей плоскость.
Приблизимся к этому вопросу следующим образом: представим, что прямая и плоскость находятся в одной системе координат. Мы можем представить каждую точку прямой с помощью вектора, который начинается в начале координат и заканчивается в точке прямой.
Точно так же, плоскость может быть задана вектором нормали к ней, который перпендикулярен этой плоскости. Вектор нормали указывает направление перпендикулярно плоскости и представляет собой нормальный вектор плоскости.
Таким образом, геометрическое представление расстояния между прямой и плоскостью состоит в нахождении неизвестного v — расстояния, которое отражает близость прямой к плоскости.
Формула расстояния
Расстояние между прямой и параллельной ей плоскостью может быть определено с помощью следующей формулы:
Формула:
- Пусть дана прямая с уравнением ax + by + cz + d = 0.
- И пусть дана параллельная ей плоскость с уравнением ax + by + cz + d₁ = 0.
Тогда расстояние d между прямой и плоскостью можно вычислить по формуле:
d = |d₁ — d| / sqrt(a² + b² + c²),
где |d₁ — d| обозначает модуль разности коэффициентов d₁ и d, а sqrt() — функция извлечения квадратного корня.
Эта формула позволяет определить расстояние между прямой и параллельной ей плоскостью, что может быть полезным при решении различных задач в геометрии и физике.
Примеры расчетов
Пример 1
Пусть дана прямая линия AB, заданная уравнением ax + by + c = 0, и параллельная ей плоскость П, заданная уравнением ax + by + d = 0. Найдем расстояние между этой прямой и плоскостью.
| Шаг | Расчеты | Результат |
|---|---|---|
| 1 | Найдем вектор нормали n плоскости П: n = (a, b) | n = (a, b) |
| 2 | Найдем коэффициенты уравнения прямой линии AB: A = a, B = b | A = a, B = b |
| 3 | Найдем расстояние d между прямой и плоскостью по формуле: d = |c — d| / sqrt(A2 + B2) | d = |c — d| / sqrt(A2 + B2) |
Пример 2
Пусть дана прямая линия CD, заданная параметрическими уравнениями x = x0 + at, y = y0 + bt, z = z0 + ct, где t — параметр, и параллельная ей плоскость П, заданная уравнением ax + by + cz + d = 0. Найдем расстояние между этой прямой и плоскостью.
| Шаг | Расчеты | Результат |
|---|---|---|
| 1 | Найдем вектор нормали n плоскости П: n = (a, b, c) | n = (a, b, c) |
| 2 | Найдем координаты начальной точки D прямой линии CD: D = (x0, y0, z0) | D = (x0, y0, z0) |
| 3 | Найдем расстояние d между прямой и плоскостью по формуле: d = |n·D + d| / sqrt(a2 + b2 + c2) | d = |n·D + d| / sqrt(a2 + b2 + c2) |
Связь с понятием векторов
Для понимания связи между расстоянием и векторами, рассмотрим следующий пример. Представим, что мы имеем параллельную плоскость и прямую, которая пересекает эту плоскость.
Если мы проведем перпендикуляр от точки на прямой до плоскости, то получим вектор, который будет перпендикулярен к плоскости. Этот вектор называется нормальным вектором плоскости. Его направление и длина играют важную роль в определении расстояния между прямой и плоскостью.
Из определения нормального вектора можно заключить, что расстояние между прямой и плоскостью равно длине проекции вектора, соединяющего две параллельные плоскости, на нормальный вектор плоскости.
Таким образом, понимание понятия векторов позволяет легче разобраться с расстоянием между прямой и параллельной ей плоскостью, а также позволяет более полно осознать и использовать его свойства при решении задач.
Применение в практике
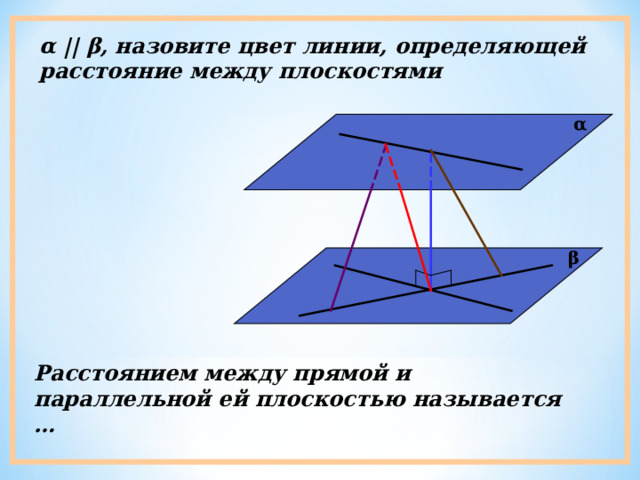
Расстояние между прямой и параллельной ей плоскостью имеет широкое применение в различных областях практики. Вот несколько примеров, где знание и использование этого понятия может быть полезным:
Архитектура и строительство
При проектировании и строительстве зданий и сооружений инженерам и архитекторам важно учитывать расстояние между прямой и параллельной плоскостью. Например, при разработке плана кровли здания необходимо учесть этот параметр для правильного расположения скатов крыши и предотвращения возможных протечек.
Машиностроение и автомобильная промышленность
В машиностроении и автомобильной промышленности расстояние между прямой и параллельной плоскостью может быть важно для определения размеров и формы деталей. Например, при проектировании двигателя автомобиля необходимо учесть этот параметр для правильной установки и расположения компонентов двигателя, чтобы обеспечить его надежную работу.
Также, знание расстояния между прямой и параллельной плоскостью может быть полезным в других областях, включая электротехнику, аэрокосмическую промышленность, судостроение, проектирование дорог и др.
В целом, понятие расстояния между прямой и параллельной плоскостью является важным и широко применяемым в различных областях практики, где точность и правильное расположение объектов являются критическими факторами.
Для вычисления расстояния необходимо знать координаты точек на прямой и в плоскости или уравнение прямой и плоскости. Существуют различные способы вычисления расстояния, в зависимости от известных данных и задачи, которую нужно решить.
Методы вычисления расстояния между прямой и параллельной ей плоскостью могут быть применены, например, в задачах оптимизации, геодезии или построении графиков в пространстве.
- Расстояние между прямой и параллельной ей плоскостью всегда положительно, так как оно измеряет фактическое расстояние между двумя объектами в пространстве.
- Вычисление расстояния требует знания координат точек прямой и плоскости или уравнений этих объектов.
- Существует несколько методов вычисления расстояния, включая прямое вычисление по формуле и использование проекций на оси координат.
- Вычисление расстояния между прямой и плоскостью может быть полезно для решения практических задач в различных областях математики и физики.
Исходя из вышеизложенного, расстояние между прямой и параллельной ей плоскостью является важным концептом, который находит применение в различных областях науки и техники.
Вопрос-ответ:
Как определить расстояние между прямой и параллельной ей плоскостью?
Расстояние между прямой и параллельной ей плоскостью можно определить как длину перпендикулярного отрезка, проведенного от точки на прямой до ближайшей точки на плоскости.
Есть ли формула для расчета расстояния между прямой и параллельной ей плоскостью?
Да, существует формула для расчета расстояния между прямой и параллельной ей плоскостью. Расстояние можно вычислить, разделив модуль уравнения плоскости на коэффициент перед неизвестной при переменной.
Какое значение имеет расстояние между прямой и параллельной ей плоскостью?
Значение расстояния между прямой и параллельной ей плоскостью может быть положительным, отрицательным или равным нулю. Положительное значение означает, что плоскость расположена ниже прямой, отрицательное — выше прямой, а ноль — что прямая и плоскость пересекаются.
Может ли расстояние между прямой и параллельной ей плоскостью быть отрицательным?
Да, расстояние между прямой и параллельной ей плоскостью может быть отрицательным. Это означает, что плоскость расположена выше прямой. В случае отрицательного расстояния, фактически, мы будем говорить о длине сегмента, который прямая пересекается с плоскостью, а не о расстоянии между ними.
Как использовать расстояние между прямой и параллельной ей плоскостью в практических задачах?
Расстояние между прямой и параллельной ей плоскостью может быть использовано, например, в геометрии для нахождения пересечений прямой и плоскости или в физике для определения взаимного расположения объектов. В практических задачах это понятие может применяться для обнаружения пересечений или определения ближайших точек одних объектов к другим.
Что такое расстояние между прямой и параллельной ей плоскостью?
Расстояние между прямой и параллельной ей плоскостью — это перпендикулярное расстояние между ними. Оно измеряется по кратчайшему пути от точки прямой до ближайшей точки на плоскости.