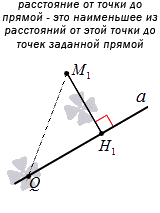
Расстояние от точки до прямой – это величина, которая показывает, насколько близко или далеко находится данная точка от прямой. Она является важным понятием в геометрии и находит свое применение в различных областях науки и техники.
Для вычисления расстояния от точки до прямой необходимо знать уравнение прямой и координаты данной точки. В случае, когда уравнение прямой задано в виде общего уравнения, расстояние можно найти по формуле, основанной на принципе подобия треугольников.
Принцип подобия треугольников основан на равенстве отношений соответствующих сторон и углов при подобии треугольников.
Определение расстояния от точки до прямой имеет огромное значение в решении различных задач. Например, в геодезии это понятие используется для определения удаленности объектов друг от друга, чаще всего в двумерном пространстве. В алгоритмах машинного зрения расстояние от точки до прямой применяется для классификации объектов и определения их положения в пространстве.
Расстояние от точки до прямой: понятие и методы вычисления
Определение расстояния от точки до прямой является важной задачей в геометрии и находит применение во многих областях, таких как физика, инженерия, компьютерная графика и другие.
Методы вычисления расстояния от точки до прямой
Существуют различные методы для вычисления расстояния от точки до прямой, в зависимости от заданной формы уравнения прямой.
Один из самых распространенных методов — это использование уравнения прямой в общем виде и формулы для расстояния от точки до прямой. Если уравнение прямой задано в виде Ax + By + C = 0, где A, B и C — известные коэффициенты, а x и y — координаты точек, то расстояние d от точки P(x0, y0) до прямой можно найти по формуле:
d = |Ax0 + By0 + C| / sqrt(A^2 + B^2)
Если же прямая задана параметрическим уравнением, то можно использовать формулу для проекции вектора и векторного произведения. В этом случае расстояние d от точки P до прямой можно найти по формуле:
d = |(P — P0) × (P — P1)| / |P1 — P0|
где P0 и P1 — точки, лежащие на прямой.
Также существуют другие способы вычисления расстояния от точки до прямой, которые удобно применять в различных задачах, включая метод наименьших квадратов, применение векторов и матриц, а также использование проекций и отражений.
Что такое расстояние от точки до прямой?
Данное расстояние имеет большое значение во многих областях науки и техники. Например, в геометрии оно используется для решения задач по построению фигур и определению их свойств. В физике и технике расстояние от точки до прямой может служить для определения оптимального маршрута движения, поиска минимального времени или определения наилучшей позиции.
Вычисление расстояния от точки до прямой зависит от уравнения прямой и координат точки. Например, для прямой, заданной уравнением y = kx + b, где k — коэффициент наклона, b — свободный член, а (x0, y0) — координаты точки, расстояние можно вычислить по формуле:
d = |k * x0 — y0 + b| / sqrt(k^2 + 1), где sqrt — корень квадратный.
Зная уравнение прямой и координаты точки, можно легко вычислить расстояние от точки до прямой и использовать его для решения различных задач и проблем.
Какое значение имеет расстояние от точки до прямой в математике?
Для вычисления расстояния от точки до прямой используется специальная формула, которая учитывает координаты точки и уравнение прямой. Расстояние может быть выражено как положительное число, и оно всегда считается со знаком. Если результат отрицательный, это означает, что точка находится на противоположной стороне от прямой по сравнению с заданной системой координат.
Формула для вычисления расстояния
Формула для вычисления расстояния от точки с координатами (x0, y0) до прямой с уравнением Ax + By + C = 0 имеет следующий вид:
d = |Ax0 + By0 + C| / √(A^2 + B^2)
Здесь d — расстояние от точки до прямой, A, B и C — коэффициенты уравнения прямой, x0 и y0 — координаты точки.
Значение расстояния от точки до прямой
Значение расстояния от точки до прямой играет важную роль в различных математических и физических задачах. Например, оно может использоваться для определения ближайшей точки на прямой к заданной точке или для нахождения расстояния до предмета на плоскости. В геометрии и физике расстояние от точки до прямой также может показать, какая сторона от прямой находится точка, и служить основой для дальнейших вычислений и решений.
Как вычислить расстояние от точки до прямой?
Чтобы вычислить расстояние от точки до прямой, используется известная формула:
Формула расстояния от точки до прямой:
Для вычисления расстояния от точки P(x0, y0) до прямой Ax + By + C = 0 можно воспользоваться следующей формулой:
| Расстояние | Формула |
|---|---|
| По модулю | d = |Ax0 + By0 + C| / sqrt(A2 + B2) |
| По координатам | d = abs(Ax0 + By0 + C) / sqrt(A2 + B2) |
Где x0 и y0 — координаты точки P, A, B и C — коэффициенты прямой, sqrt — функция квадратного корня, а abs — функция модуля числа.
Подставив значения координат точки и коэффициенты прямой в формулу, можно вычислить расстояние от точки до прямой.
Например, если имеется точка P(2, 3) и прямая 2x + 3y — 6 = 0, то расстояние от точки до прямой будет:
d = |2 * 2 + 3 * 3 — 6| / sqrt(22 + 32)
После подсчета получим окончательное значение расстояния от точки до прямой.
Таким образом, вычисление расстояния от точки до прямой позволяет определить, насколько близко или далеко находится точка от прямой, что может быть полезно при решении различных задач и анализе данных.
Геометрический подход к вычислению расстояния от точки до прямой
В геометрии расстояние от точки до прямой определяется как минимальное расстояние между точкой и прямой. Для нахождения этого расстояния можно использовать геометрический подход, который позволяет найти перпендикуляр к прямой, проходящий через заданную точку, и измерить длину этой перпендикуляра.
Для вычисления расстояния от точки до прямой можно использовать следующие шаги:
- Найти уравнение прямой в общем виде.
- Найти координаты точки, от которой вычисляется расстояние.
- Найти уравнение перпендикуляра к прямой, проходящего через данную точку. Для этого необходимо найти отрицательную обратную величину коэффициента наклона прямой и подставить в уравнение перпендикуляра координаты точки.
- Найти точку пересечения прямой и перпендикуляра.
- Измерить расстояние между этой точкой и исходной точкой.
Таким образом, геометрический подход позволяет точно определить расстояние от заданной точки до прямой, используя геометрические принципы и уравнение прямой.
Аналитический метод вычисления расстояния от точки до прямой
Общая формула
Для нахождения расстояния от точки до прямой с помощью аналитического метода применяется следующая формула:
d = |Ax + By + C| / sqrt(A^2 + B^2)
Где:
- d — расстояние от точки до прямой.
- A, B, C — коэффициенты общего уравнения прямой Ax + By + C = 0.
- x, y — координаты точки.
- sqrt — функция, возвращающая квадратный корень.
- | | — обозначает модуль числа.
Порядок вычисления
Чтобы получить расстояние от точки до прямой, необходимо вставить значения A, B, C и координаты точки в формулу и выполнить необходимые арифметические операции.
Пример:
- Прямая задана уравнением 2x + 3y — 4 = 0.
- Точка имеет координаты (1, -2).
- Расстояние будет равно |2*1 + 3*(-2) — 4| / sqrt(2^2 + 3^2).
- Расстояние составляет 3,21 единицы.
Таким образом, аналитический метод позволяет вычислить расстояние от точки до прямой на плоскости, используя заранее известные коэффициенты прямой и координаты точки.
Как использовать формулу для вычисления расстояния от точки до прямой?
Шаг 1: Определение уравнения прямой
Прежде чем вычислять расстояние от точки до прямой, необходимо определить уравнение самой прямой. Уравнение прямой может быть задано в различных формах, например, в виде общего уравнения прямой Ax + By + C = 0 или в виде уравнения прямой, проходящей через две точки. Важно знать какую форму уравнения используете, чтобы правильно применить формулу расстояния.
Шаг 2: Вычисление расстояния
После определения уравнения прямой и задания точки, для которой необходимо найти расстояние, можно перейти к вычислению расстояния. Формула для вычисления расстояния от точки до прямой имеет следующий вид:
| Расстояние от точки до прямой: | d = |Ax + By + C| / √(A^2 + B^2) |
где A, B и C — коэффициенты уравнения прямой, а x и y — координаты точки, для которой вычисляется расстояние.
Применяя эту формулу, можно найти расстояние от любой точки до заданной прямой и использовать его в различных математических и геометрических задачах.
Практические примеры вычисления расстояния от точки до прямой
Для вычисления данного расстояния использование уравнения прямой и координат точки. Рассмотрим несколько практических примеров.
Пример 1:
Дана прямая, заданная уравнением 2x + 3y — 6 = 0, и точка A(4, 2). Необходимо найти расстояние от точки до прямой.
1. Найдем угловой коэффициент прямой из её уравнения:
Уравнение прямой: 2x + 3y — 6 = 0
Разрешим его относительно y:
y = (6 — 2x) / 3
Угловой коэффициент равен коэффициенту при x в уравнении.
2. Найдем перпендикуляр к прямой, проходящий через точку A(4, 2).
Уравнение перпендикуляра имеет вид: y = -x/2 + b.
Заменим координаты точки A(4, 2) в уравнении и найдем коэффициент b.
2 = -4/2 + b
2 = -2 + b
b = 4
3. Из уравнения перпендикуляра y = -x/2 + 4 и уравнения прямой 2x + 3y — 6 = 0 найдем точку пересечения.
Подставим уравнение перпендикуляра в уравнение прямой:
2x + 3(-x/2 + 4) — 6 = 0
2x — 3x/2 + 12 — 6 = 0
-x/2 — 3x/2 = -6 + 12
-4x/2 = 6
-2x = 6
x = -3
Подставим найденное значение x в уравнение перпендикуляра:
y = -(-3)/2 + 4
y = 3/2 + 4
y = 11/2
Таким образом, точка пересечения прямой и перпендикуляра равна B(-3, 11/2).
4. Найдем расстояние между точками A(4, 2) и B(-3, 11/2) при помощи формулы:
d = sqrt((x2 — x1)^2 + (y2 — y1)^2)
d = sqrt((-3 — 4)^2 + (11/2 — 2)^2)
d = sqrt((-7)^2 + (7/2)^2)
d = sqrt(49 + 49/4)
d = sqrt(196/4 + 49/4)
d = sqrt(245/4)
d = 7*sqrt(5)/2
Таким образом, расстояние от точки A(4, 2) до прямой 2x + 3y — 6 = 0 равно 7*sqrt(5)/2.
Пример 2:
Дана прямая, проходящая через точки A(1, 4) и B(5, 2), и точка C(3, 6). Необходимо найти расстояние от точки до прямой.
1. Найдем угловой коэффициент прямой при помощи координат точек A(1, 4) и B(5, 2):
k = (y2 — y1) / (x2 — x1)
k = (2 — 4) / (5 — 1)
k = (-2) / 4
k = -1/2
2. Найдем перпендикуляр к прямой, проходящий через точку C(3, 6).
Уравнение перпендикуляра имеет вид: y = -1/k * x + b.
Заменим координаты точки C(3, 6) в уравнении и найдем коэффициент b:
6 = -1/(-1/2) * 3 + b
6 = 6 + b
b = 0
3. Найдем точку пересечения прямой и перпендикуляра.
Подставим уравнение перпендикуляра в уравнение прямой:
y = -1/2 * x + 0
2x + 3(-1/2 * x) — 6 = 0
2x — 3/2 * x — 6 = 0
4x — 3x — 12 = 0
x — 12 = 0
x = 12
Подставим найденное значение x в уравнение перпендикуляра:
y = -1/2 * 12 + 0
y = -6 + 0
y = -6
Таким образом, точка пересечения прямой и перпендикуляра равна D(12, -6).
4. Найдем расстояние между точками C(3, 6) и D(12, -6) при помощи формулы:
d = sqrt((x2 — x1)^2 + (y2 — y1)^2)
d = sqrt((12 — 3)^2 + (-6 — 6)^2)
d = sqrt(9^2 + (-12)^2)
d = sqrt(81 + 144)
d = sqrt(225)
d = 15
Таким образом, расстояние от точки C(3, 6) до прямой, проходящей через точки A(1, 4) и B(5, 2), равно 15.
Как применяют расстояние от точки до прямой в реальной жизни?
Физика и астрономия
В физике и астрономии расстояние от точки до прямой может использоваться для определения положения и движения объектов. Например, при изучении движения планеты или спутника относительно Земли, можно найти расстояние от точки на орбите до линии горизонта.
Компьютерная графика и технологии

В компьютерной графике расстояние от точки до прямой используется для определения положения и формы объектов на экране. Это позволяет создавать реалистичные трехмерные модели и анимации. Например, при создании компьютерных игр или виртуальной реальности, расстояние от точки до прямой позволяет определить, какой объект находится ближе к наблюдателю или камере.
Важно отметить, что применение расстояния от точки до прямой в реальной жизни не ограничивается перечисленными областями. Оно также используется в навигации, архитектуре, обработке изображений, инженерии и других сферах.
Вопрос-ответ:
Как определить расстояние от точки до прямой?
Расстояние от точки до прямой можно определить с помощью формулы, называемой формулой расстояния от точки до прямой. Для этого нужно знать координаты точки и уравнение прямой, к которой нужно найти расстояние. Подставив значения в формулу, можно вычислить расстояние.
Зачем нужно находить расстояние от точки до прямой?
Найти расстояние от точки до прямой может потребоваться в различных математических и геометрических задачах. Например, при построении перпендикуляра к прямой, которая проходит через заданную точку, необходимо знать расстояние от этой точки до прямой. Также это может быть полезно в физике, геодезии, строительстве и других областях.
Какая формула позволяет найти расстояние от точки до прямой?
Формула, позволяющая найти расстояние от точки до прямой, зависит от способа задания прямой. Для прямой в общем виде (Ax + By + C = 0) формула имеет вид: d = |Ax + By + C| / sqrt(A^2 + B^2), где (x, y) — координаты точки, d — искомое расстояние. Для прямой, заданной двумя точками, формула выглядит следующим образом: d = |Ax0 + By0 + C| / sqrt(A^2 + B^2), где (x0, y0) — координаты одной из точек прямой.
Можно ли вычислить расстояние от точки до прямой без знания уравнения прямой?
Да, расстояние от точки до прямой можно вычислить без знания уравнения прямой. Для этого нужно знать координаты двух точек, через которые проходит прямая. Затем можно воспользоваться формулой для расстояния между двумя точками и посчитать расстояние от заданной точки до прямой.
Можно ли найти расстояние от точки до прямой на плоскости?
Да, можно. Расстояние от точки до прямой на плоскости можно найти с помощью специальной формулы. В этой формуле учитываются координаты точки и уравнение прямой. Подставив значения в формулу, можно вычислить расстояние от точки до прямой на плоскости.