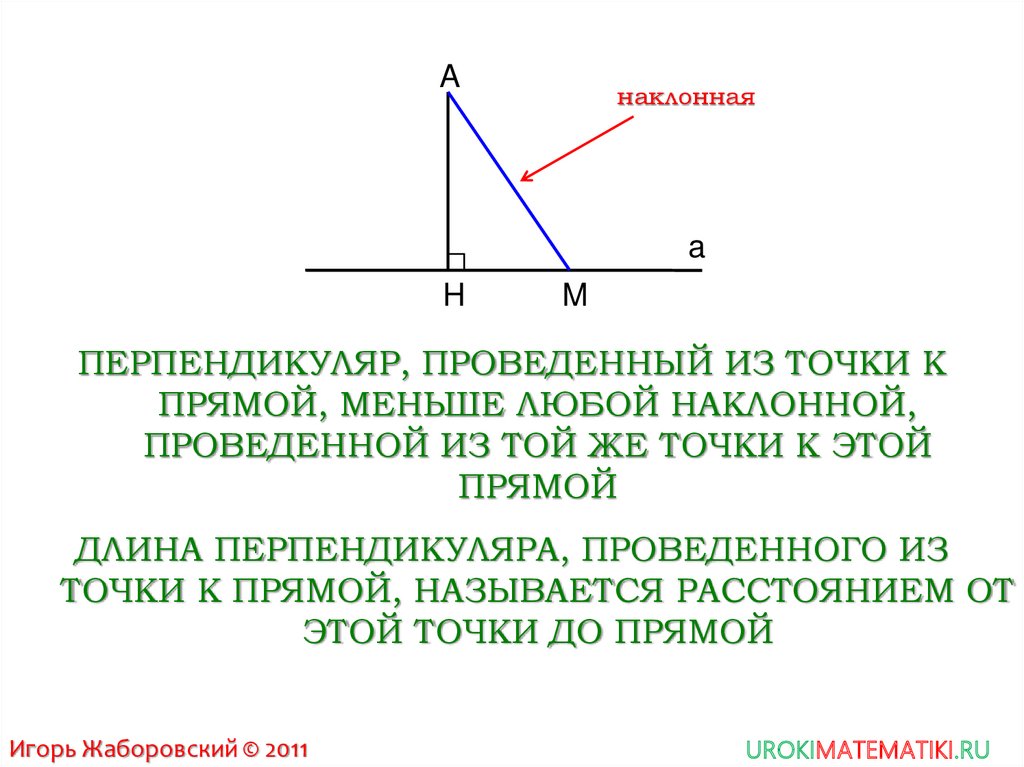
Расстояние от точки до прямой является важной геометрической величиной, которая позволяет измерить удаленность точки от прямой. Это понятие активно применяется в различных областях науки и техники, таких как математика, физика, инженерия и др. Расстояние от точки до прямой может быть положительным, отрицательным или равным нулю в зависимости от их взаимного положения.
Расчет расстояния от точки до прямой основан на использовании формулы, которая учитывает координаты точки и уравнение прямой. Для выполнения такого расчета необходимо знание базовых понятий и методов аналитической геометрии, включая понимание проекции, векторов и уравнений прямых.
Расстояние от точки до прямой может быть интерпретировано как длина кратчайшего пути от точки до прямой. Это может быть полезно в задачах оптимизации, где требуется минимизировать расстояние между точками и прямыми, либо в геодезии, когда необходимо измерить удаленность между объектами на поверхности Земли.
Что такое расстояние от точки до прямой?
Часто в задачах геометрии и математике требуется найти расстояние от точки до прямой для решения определенных задач или построения графиков. Для этого применяются специальные формулы и методы расчета.
Как найти расстояние от точки до прямой?
Существует несколько способов вычисления расстояния от точки до прямой, в зависимости от заданных условий и доступных данных. Одним из наиболее часто используемых методов является использование формулы, основанной на применении векторов и проекций.
Для нахождения расстояния необходимо знать уравнение прямой и координаты заданной точки. Затем используя формулу, можно вычислить нужное расстояние. Формула может быть представлена разными способами в зависимости от типа прямой (например, вертикальной, горизонтальной или наклонной).
Значение расстояния от точки до прямой
Расстояние от точки до прямой всегда является положительным числом, так как оно измеряется длиной отрезка. Чем больше значение расстояния, тем дальше точка находится от прямой, а чем меньше значение, тем ближе она к ней.
Расстояние от точки до прямой является важным понятием в геометрии и находит свое применение в различных областях, таких как аналитическая геометрия, физика, статистика и другие.
Как определить расстояние от точки до прямой?
Шаг 1: Запишите уравнение прямой
Для начала необходимо иметь уравнение прямой, до которой нужно найти расстояние. Уравнение прямой может быть задано в различной форме, например, в виде уравнения прямой в пространстве или уравнения прямой на плоскости. Общая форма уравнения прямой на плоскости имеет вид:
ax + by + c = 0
где a, b и c — коэффициенты, определяющие прямую.
Шаг 2: Запишите координаты точки
Теперь необходимо знать координаты точки, до которой будет определяться расстояние. Координаты точки обычно задаются в виде пары чисел (x, y), где x — координата по горизонтали (ось X), y — координата по вертикали (ось Y).
Шаг 3: Примените формулу для расстояния
После заполнения первых двух шагов можно приступить к определению расстояния. Для этого существует специальная формула:
d = |ax + by + c| / sqrt(a^2 + b^2)
где d — искомое расстояние от точки до прямой.
Подставьте значения коэффициентов a, b, c и координаты точки x, y в формулу и вычислите результат.
Таким образом, зная уравнение прямой и координаты точки, вы можете определить расстояние от точки до прямой. Этот метод полезен при решении различных задач, связанных с геометрией или анализом данных.
Методы вычисления расстояния от точки до прямой
Метод 1: Формула расстояния от точки до прямой
В рамках этого метода расстояние от точки \(A(x_1, y_1)\) до прямой \(Ax + By + C = 0\) может быть вычислено по следующей формуле:
\[d = \frac{{\left|Ax_1 + By_1 + C
ight|}}{{\sqrt{{A^2 + B^2}}}}\]
Здесь \(d\) — искомое расстояние.
Метод 2: Формула площади параллелограмма
Также можно воспользоваться методом, основанным на нахождении площади параллелограмма, образованного отрезком, проведенным от точки до прямой, и линиями, перпендикулярными прямой. Расстояние от точки до прямой будет равно длине этого отрезка.
Определяется площадь параллелограмма следующим образом:
\[S = \frac{{\left|Ax_1 + By_1 + C
ight|}}{2}\]
Тогда расстояние от точки до прямой можно найти по формуле:
\[d = \frac{{2S}}{{\sqrt{{A^2 + B^2}}}}\]
Где \(d\) — искомое расстояние.
Зачем нужно знать расстояние от точки до прямой?
Геометрия
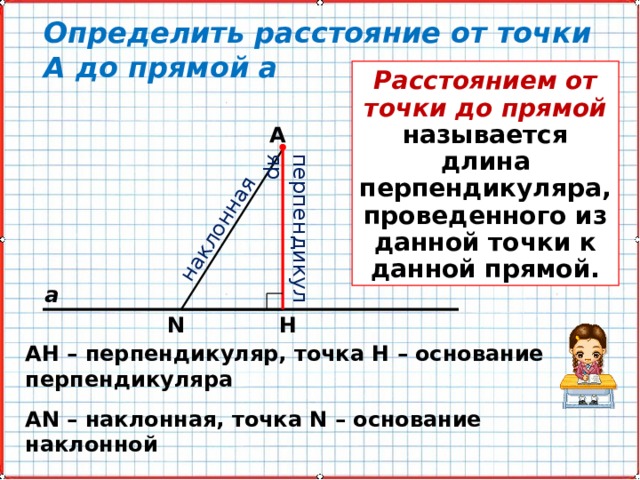
В геометрии расстояние от точки до прямой позволяет определить положение точки относительно прямой. Например, зная расстояние от точки до прямой, можно определить, находится ли точка на прямой, вне прямой или внутри ее. Это полезно для решения задач по построению фигур или определению взаимного расположения геометрических объектов.
Физика и инженерия
В физике и инженерии знание расстояния от точки до прямой помогает решать задачи, связанные с движением объектов или конструкцией различных устройств. Например, при проектировании мостов или строительстве дорог необходимо учитывать расстояние от точки до прямой, чтобы определить оптимальное расположение объектов и обеспечить безопасность конструкции.
Кроме того, в физике расстояние от точки до прямой позволяет определить путь, который должен пройти объект, чтобы переместиться от одной точки к другой. Это полезно при решении задач по прогнозированию траекторий движения или определению пути наиболее эффективного перемещения.
Информатика и компьютерная графика
В информатике и компьютерной графике знание расстояния от точки до прямой позволяет решать задачи по визуализации данных, определению положения объектов на экране или поиску ближайшей точки к заданной прямой. Например, это может быть полезно при разработке компьютерных игр, создании алгоритмов для работы с графическими объектами или анализе больших объемов данных.
Таким образом, знание расстояния от точки до прямой помогает решать множество задач в различных областях наук и применяется как базовый инструмент для работы с геометрическими и числовыми данными.
| Примеры применения | Описание |
|---|---|
| Геометрическое построение | Определение положения точки относительно прямой для построения фигур |
| Строительство и инженерия | Оптимальное расположение объектов и безопасность конструкций |
| Физика | Определение пути движения объектов и прогнозирование траекторий |
| Информатика и компьютерная графика | Визуализация данных, поиск ближайших точек и определение положения объектов |
Расстояние от точки до прямой в геометрии
Для вычисления расстояния от точки до прямой используется формула, основанная на математическом аппарате и уравнениях прямой. Существуют различные способы вычисления расстояния в зависимости от формы уравнения прямой.
Способ 1: Вычисление расстояния от точки до прямой по координатам
Если уравнение прямой задано в декартовой системе координат (x, y), то для вычисления расстояния от точки (x1, y1) до прямой можно воспользоваться формулой:
d = |Ax1 + By1 + C| / √(A^2 + B^2)
где A, B и C — коэффициенты уравнения прямой, а x1 и y1 — координаты точки.
Способ 2: Вычисление расстояния от точки до прямой по уравнению прямой
Если уравнение прямой задано явно, то есть в виде функции y = f(x) или x = g(y), то для вычисления расстояния от точки (x1, y1) до прямой можно воспользоваться формулой:
d = |f(x1) — y1| / √(1 + f'(x1)^2)
где f(x1) — значение функции прямой в точке x1, y1 — значение y в точке, а f'(x1) — производная функции в точке x1.
Вычисление расстояния от точки до прямой имеет множество практических применений в различных областях, таких как физика, инженерия, компьютерная графика и многое другое.
Геометрическое обоснование расстояния от точки до прямой
Представим, что у нас есть точка \(P\), заданная своими координатами \((x_0, y_0)\), и прямая \(l\), заданная уравнением \(Ax + By + C = 0\), где \(A\), \(B\) и \(C\) — константы.
Чтобы найти расстояние от точки до прямой, необходимо найти точку \(Q\) на прямой, ближайшую к точке \(P\). Можно заметить, что вектор \(\overrightarrow{PQ}\) будет перпендикулярен прямой \(l\), а значит, его направляющий вектор будет коллинеарен вектору \((A, B)\).
Используя это свойство, мы можем записать вектор \(\overrightarrow{PQ}\) в виде \(\overrightarrow{PQ} = t(A, B)\), где \(t\) — некоторый параметр.
Так как вектор \(\overrightarrow{PQ}\) перпендикулярен прямой \(l\), то проекция вектора \(\overrightarrow{PQ}\) на нормальный вектор \((A, B)\) будет равна нулю. Из этого следует, что произведение скалярных проекций \((A, B)\) и \(\overrightarrow{PQ}\) должно равняться нулю: \(A \cdot \overrightarrow{PQ_x} + B \cdot \overrightarrow{PQ_y} = 0\).
Подставим вектор \(\overrightarrow{PQ} = t(A, B)\) и координаты точки \(P\) в выражение для скалярного произведения: \(A \cdot t(A, B)_x + B \cdot t(A, B)_y = 0\).
Раскроем скобки и получим уравнение \(At^2 + Bt^2 = Cx_0 t + Cy_0 t\).
Домножим это уравнение на коэффициент при \((Cx_0 + Cy_0)\) для того, чтобы избавиться от дробей: \((A^2 + B^2)t^2 = (Cx_0 + Cy_0)t\).
Окончательно, найдем значение параметра \(t\), подставив координаты точки \(P\) в уравнение и разделив обе части на \((A^2 + B^2)\): \(t = \frac{Cx_0 + Cy_0}{A^2 + B^2}\).
Зная значение параметра \(t\), мы можем вычислить координаты точки \(Q\) на прямой при помощи формулы \(\overrightarrow{PQ} = t(A, B)\) и расстояние от точки \(P\) до прямой \(\overline{PQ}\) при помощи формулы Евклида.
| Координаты точки \(P\) | Уравнение прямой \(l\) | Найденная точка \(Q\) | Расстояние от точки \(P\) до прямой |
|---|---|---|---|
| \((x_0, y_0)\) | \(Ax + By + C = 0\) | \(\left(\frac{Cx_0 + Cy_0}{A^2 + B^2}, \frac{Cx_0 + Cy_0}{A^2 + B^2} ight)\) | \(\sqrt{\left(\frac{Cx_0 + Cy_0}{A^2 + B^2} ight)^2 + \left(\frac{Ax_0 + By_0}{A^2 + B^2} ight)^2}\) |
Таким образом, геометрическое обоснование расстояния от точки до прямой позволяет вычислить минимальное расстояние между двумя объектами в пространстве, используя при этом геометрические свойства и формулы.
Расстояние от точки до прямой в плоскости
Для нахождения расстояния от точки до прямой требуется знать координаты точки, координаты двух точек на прямой или уравнение прямой.
Существует несколько способов нахождения расстояния от точки до прямой. Один из них основывается на формуле, которая выражает расстояние через координаты точек.
Пусть дана точка P(x0, y0) и прямая ax + by + c = 0. Тогда расстояние d от точки до прямой может быть найдено по формуле:
d = | ax0 + by0 + c | / sqrt(a2 + b2)
Знак модуля используется, чтобы результат всегда был положительным числом.
Таким образом, в решении геометрических задач, связанных с определением расстояния от точки до прямой, можно использовать данную формулу.
Апробация методов вычисления расстояния от точки до прямой
В математике существует несколько способов вычисления расстояния от точки до прямой. Развитие компьютерной техники и программного обеспечения позволило применить эти методы на практике для решения различных инженерных и научных задач.
Один из наиболее распространенных методов вычисления расстояния от точки до прямой основан на использовании уравнения прямой в общем виде и координат точки.
Другим применяемым методом является использование уравнения перпендикуляра, опущенного из точки на прямую. Данное уравнение позволяет определить координаты точки пересечения перпендикуляра с прямой, от которых можно вычислить расстояние от начальной точки до прямой.
Также стоит упомянуть метод, основанный на использовании векторов. По заданным координатам точки и прямой можно вычислить векторы от точки до прямой, и затем вычислить их скалярное произведение для определения расстояния.
Каждый из этих методов имеет свои преимущества и ограничения, и их выбор зависит от конкретной задачи. Апробация и сравнение этих методов на различных компьютерных моделях позволяет выбрать наиболее эффективный подход к решению задачи вычисления расстояния от точки до прямой.
Вопрос-ответ:
Что такое расстояние от точки до прямой?
Расстояние от точки до прямой – это длина отрезка, проведенного перпендикулярно к данной прямой от этой точки до самой прямой.
Как вычислить расстояние от точки до прямой?
Для вычисления расстояния от точки до прямой следует провести перпендикуляр от данной точки к прямой и измерить длину этого перпендикуляра.
В чем заключается геометрический смысл расстояния от точки до прямой?
Геометрический смысл расстояния от точки до прямой заключается в том, что это расстояние показывает, насколько близко или далеко от данной точки находится самая ближайшая точка на прямой.
Как применяется расстояние от точки до прямой в реальной жизни?
Расстояние от точки до прямой имеет множество применений в реальной жизни, например, в навигации для определения ближайшей точки маршрута, в архитектуре для размещения объектов на оптимальном расстоянии от прямой или в физике для измерения расстояния между двумя объектами.
Можно ли выразить расстояние от точки до прямой аналитически?
Да, расстояние от точки до прямой можно выразить аналитически с помощью формулы, которая зависит от уравнения данной прямой и координат точки.
Как определить расстояние от точки до прямой?
Расстояние от точки до прямой можно определить с помощью формулы, которая основана на известных координатах точки и уравнении прямой. Формула выглядит так: d = |Ax + By + C| / sqrt(A^2 + B^2), где A, B и C — это коэффициенты уравнения прямой, а x и y — координаты точки.