
Векторы – это одно из основных понятий в линейной алгебре. Они используются для представления и описания физических величин, таких как сила, скорость, смещение и другие. Особенность векторов заключается в том, что они имеют не только величину, но и направление. Именно поэтому векторы называются равными, если они сонаправлены, то есть имеют одно и то же направление.
Чтобы визуализировать векторы, используются стрелки, которые начинаются в точке начала вектора и указывают на его направление и величину. Длина стрелки отражает величину вектора, а направление стрелки – его направление. Если два вектора обладают одинаковой длиной и указывают в одном и том же направлении, то они называются сонаправленными векторами.
Сонаправленные векторы могут иметь одинаковую или противоположную ориентацию. Если два вектора имеют не только одно и то же направление, но и одинаковую ориентацию (то есть оба направлены в одну сторону), то они называются полностью равными. Если же они имеют противоположную ориентацию (то есть оба направлены в противоположные стороны), то они называются обратно равными. В обоих случаях векторы считаются сонаправленными, так как имеют одно и то же направление.
Понятие равенства векторов
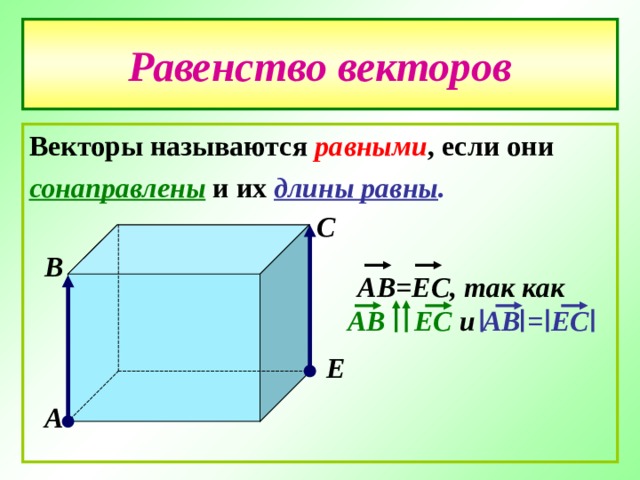
Векторы называются равными, если они сонаправлены и имеют одинаковую длину. Это означает, что у двух векторов совпадает направление и величина. Если два вектора A и B равны, то их компоненты по каждой оси также будут совпадать.
Равенство векторов можно проверить с помощью различных методов. Один из них — сравнение компонентов векторов. Если все компоненты двух векторов совпадают, то они равны. Альтернативным методом является сравнение модулей векторов. Если модули двух векторов равны, то они сонаправлены и равны.
Пример:
Заключение:
Понятие равенства векторов играет важную роль в линейной алгебре. Проверка равенства векторов позволяет установить, совпадают ли два вектора или нет.
Основные свойства равных векторов
Основные свойства равных векторов:
- Модуль равных векторов равен.
- Направление равных векторов совпадает.
- Сумма или разность равных векторов также будет равна равному вектору с тем же самым модулем и направлением.
- Кратный вектор равен вектору с модулем, равным произведению модуля равного вектора на число.
- Равные векторы можно указать графически с помощью стрелок, которые имеют одинаковую длину и направление.
Свойства равных векторов широко применяются в физике и математике для анализа и описания физических и геометрических явлений.
Методы проверки равенства векторов
Векторы, сонаправленные и одинаковой длины, считаются равными. Существуют различные методы проверки равенства векторов:
| Метод | Описание |
|---|---|
| Метод сравнения координат | Для проверки равенства векторов сравниваются их координаты. Если все координаты одного вектора равны координатам другого вектора, то они считаются равными. |
| Метод сравнения модулей | Векторы равны, если их модули равны. Модуль вектора – это длина вектора и может быть вычислен как квадратный корень из суммы квадратов его координат. |
| Метод углов | Векторы равны, если угол между ними равен нулю. Угол между двумя векторами можно найти с помощью скалярного произведения векторов. Если скалярное произведение равно произведению модулей векторов, то угол между векторами равен нулю. |
Эти методы позволяют проверить равенство векторов и применяются в различных областях, включая физику, геометрию и программирование.
Приложение равенства векторов в физике

Равенство векторов играет важную роль в физике, поскольку позволяет определить, насколько два вектора сонаправлены и тем самым оценить степень их схожести, важной характеристики во многих физических задачах.
Сонаправленные векторы
Векторы называются сонаправленными, если они имеют одинаковую или противоположную направленность. Это означает, что два сонаправленных вектора расположены вдоль одной прямой, а их направления совпадают или противоположны.
Определение равенства векторов основано на концепции сонаправленности. Два вектора A и B считаются равными, если они сонаправлены и имеют одинаковую или противоположную длину, то есть их модули равны или отличаются только знаком.
Применение равенства векторов
Понятие равенства векторов широко применяется в физике для решения различных задач. Например, при анализе сил, действующих на тело, равенство векторов используется для определения равновесия системы или расчета результирующей силы.
Также равенство векторов позволяет проводить операции с векторами, такие как сложение и вычитание. Если два вектора равны, то их сумма будет равна удвоенному вектору, а разность — нулевому вектору.
Важно отметить, что равенство векторов — это не только схожесть направления, но и равенство длины. Это позволяет определить, насколько два вектора совпадают или отличаются по масштабу.
Взаимосвязь равенства векторов и их модулей
Условия равенства векторов:
- Векторы должны быть сонаправлены – это означает, что они должны указывать в одном и том же направлении. Если векторы направлены в противоположные стороны, они не могут быть равными.
- Модули векторов должны быть равными – это означает, что длины векторов должны быть одинаковыми. Модуль вектора – это его длина, которая может быть найдена при помощи специальных формул.
Однако следует отметить, что равные векторы могут располагаться в разных точках пространства. Важно понимать, что равенство векторов определяется не только их направлением и длиной, но также и их начальной точкой.
Примеры равных векторов:
| Вектор A | Вектор B |
|---|---|
 |  |
| Модуль: 5 ед. | Модуль: 5 ед. |
Как видно из примера, векторы A и B сонаправлены и имеют одинаковую длину, поэтому они считаются равными.
Взаимосвязь равенства векторов и их модулей важна при решении задач и проведении вычислений в физике, математике и других науках. При нахождении равных векторов необходимо учесть их направление и длину, а также возможную разницу в их начальной точке.
Различия равенства векторов и сонаправленности
Равенство векторов
Векторы называются равными, если они имеют одинаковую длину и направление. Математически это выражается так:
Если A и B — векторы, то A = B, если |A| = |B| и A // B, где || — обозначает длину вектора, // — параллельность векторов.
Равенство векторов означает, что они представляют один и тот же физический объект или имеют одинаковую величину и направление.
Сонаправленность векторов
Сонаправленными векторами называются векторы, которые имеют одинаковое или противоположное направление, но могут иметь различную длину. Это позволяет выделить только общую тенденцию или направление движения векторов.
Например, векторы A = (3, 2) и B = (6, 4) сонаправлены, так как они указывают в одном и том же направлении, но вектор B имеет удвоенную длину по сравнению с вектором A.
Сонаправленность векторов позволяет анализировать только направления и тенденции векторов, но не учитывает разницу в их величинах.
Таким образом, равенство векторов означает не только сонаправленность, но и одинаковую длину. В то время как сонаправленность векторов учитывает только общее направление без учета их длин.
Равенство векторов и линейная зависимость
Для определения равенства двух векторов необходимо проверить, сонаправлены они или нет. Векторы называются равными, если они имеют одинаковые направления и длины. Если векторы имеют разные направления или разные длины, то они считаются неравными.
Линейная зависимость векторов означает, что один из векторов может быть выражен через линейную комбинацию других векторов. Другими словами, существует такой набор коэффициентов, при умножении на которые каждый вектор можно получить суммируя все векторы с этими коэффициентами.
Линейная зависимость определяется следующим образом: если существует набор чисел, не все из которых равны нулю, такой что их линейная комбинация равна нулевому вектору, то говорят, что векторы линейно зависимы.
Если же никакой ненулевой линейной комбинации векторов не соответствует нулевой вектор, то векторы называются линейно независимыми.
Определение равенства векторов и линейной зависимости является одним из фундаментальных понятий линейной алгебры и находит широкое применение в различных областях науки и техники.
Вопрос-ответ:
Что такое векторы?
Векторы — это математические объекты, которые характеризуются направлением и длиной. Они часто используются для представления физических величин, таких как скорость, ускорение и сила.
Как определить, что два вектора сонаправлены?
Два вектора сонаправлены, если они имеют одинаковое направление или противоположное направление. Для проверки сонаправленности можно использовать следующий метод: умножить координаты первого вектора на координаты второго. Если результат равен нулю, то векторы сонаправлены.
Что значит, что векторы равны друг другу?
Векторы называются равными, если они имеют одинаковую длину и направление. Другими словами, если все компоненты одного вектора равны соответствующим компонентам другого вектора, то они считаются равными.
Можно ли сравнивать векторы, имеющие разные длины?
Да, векторы можно сравнивать, даже если они имеют разные длины. Векторы будут считаться равными, если они сонаправлены, независимо от их длины. Однако, если вам требуется сравнить векторы, учитывая их длину, можно использовать другие алгоритмы или метрики расстояния, такие как евклидово расстояние.
Какие еще операции можно выполнять с векторами?
С векторами можно выполнять множество операций. К ним относятся сложение векторов, умножение вектора на скаляр, нахождение скалярного произведения, нахождение векторного произведения, нахождение угла между векторами и другие.
Что такое векторы?
Векторы — это математические объекты, которые характеризуются направлением и длиной.