
Вектор – одно из ключевых понятий в линейной алгебре и математическом анализе. Вектор может быть определен как направленный отрезок, который имеет определенную длину и направление. Векторы используются в различных областях науки и техники, таких как физика, информатика, инженерия и многие другие.
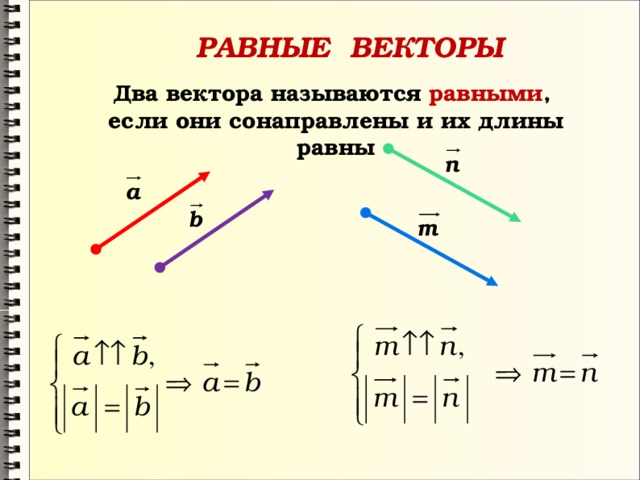
Два вектора называются равными, если они имеют одинаковую длину и направление. Векторы могут быть представлены в виде математических объектов, которые задаются числовыми значениями и описываются с помощью компонентов. Векторы могут быть заданы как в прямоугольной системе координат, так и в полярной системе координат.
Чтобы проверить, являются ли два вектора равными, необходимо сравнить их компоненты. Если все компоненты одного вектора равны соответствующим компонентам другого вектора, то они считаются равными. В противном случае, если хотя бы одна компонента отличается, то векторы не могут быть считаться равными.
Что такое равные векторы?
Векторы называются равными, если они имеют одинаковую длину и направление. Равные векторы могут быть сдвинуты в пространстве, но их длина и направление остаются неизменными.
Для определения равенства векторов необходимо проверить два условия:
- Длина векторов должна быть одинаковой. Для этого можно использовать формулу вычисления длины вектора:
|AB| = √((x2 — x1)2 + (y2 — y1)2) - Направление векторов должно быть одинаковым. Для проверки совпадения направлений можно использовать координатные углы векторов. Если координатные углы v1 и v2 равны, то векторы считаются равными. Также направление вектора можно проверить с помощью анализа координатных компонент. Если компоненты векторов равны, то направления векторов также равны.
Равные векторы имеют одинаковые свойства и характеристики, поэтому они могут быть использованы в различных математических и физических задачах.
Суть понятия равных векторов
Векторы в математике играют важную роль и представляют собой направленную отрезок, который характеризуется своей длиной и направлением. Два вектора называются равными, если они имеют одинаковые длину и направление.
Сравнение векторов на равенство происходит по двум параметрам: длине и направлению. Если два вектора имеют разную длину или разное направление, то они считаются неравными.
Определение равенства векторов позволяет производить различные операции с векторами, такие как сложение, вычитание, умножение на скаляр и другие. Если векторы равны, то результат этих операций также будет равным вектором, имеющим ту же длину и направление.
Суть понятия равных векторов заключается в их идентичности по длине и направлению. Это позволяет применять математические операции к векторам и получать корректные результаты.
Математическая запись равных векторов
В математике векторы могут быть равными, если они имеют одинаковое направление и длину. Запись равенства векторов происходит с помощью специальных символов и математических обозначений.
Равенство векторов записывается с помощью символа «=». Например, если у нас есть два вектора A и B, и они равны друг другу, запись будет выглядеть следующим образом:
A = B
Также можно использовать стрелки над буквами векторов для обозначения равенства. Например, запись вектора AB равна вектору CD будет выглядеть следующим образом:
AB ⇌ CD
При записи равенства векторов можно использовать математические обозначения для указания длины и направления вектора. Например, если у нас есть вектор A, который имеет направление и длину (2, 3), а вектор B имеет направление и длину (2, 3), и они равны друг другу, запись будет выглядеть следующим образом:
| Вектор | Координаты |
|---|---|
| A | (2, 3) |
| B | (2, 3) |
Это означает, что векторы A и B состоят из одинаковых координат и имеют одинаковую длину и направление.
Свойства равных векторов
Равные векторы обладают следующими свойствами:
- Равные векторы имеют одинаковые координаты.
- Равные векторы имеют одинаковую длину и направление.
- Равные векторы могут быть сдвинуты друг относительно друга, но останутся равными.
- Равные векторы могут быть умножены на скаляр, и результат будет равным.
Знание математической записи равных векторов позволяет более точно описывать и решать задачи, связанные с векторами и их равенством в математике и физике.
Операции с равными векторами
Сложение равных векторов:
Сумма двух равных векторов будет равна вектору, у которого длина и направление такие же, как у исходных векторов. Можно представить это так: если двигаться по первому вектору и затем по второму вектору, то конечная точка будет находиться на продолжении исходной линии.
Пример:
Пусть у нас есть два равных вектора: в и г. Их сумма будет равна вектору с, у которого длина и направление такие же.
в + г = с
Таким образом, сложение равных векторов приводит к получению нового вектора, который также будет равен исходным.
Вычитание равных векторов:
Разность двух равных векторов будет равна нулевому вектору. Это означает, что конечная точка при вычитании равных векторов совпадает с начальной точкой.
Пример:
Пусть наш исходный вектор а и вектор b также равен а. Тогда разность векторов будет равна нулевому вектору:
а — b = 0
Таким образом, при вычитании равных векторов, мы получаем нулевой вектор.
Понимание операций с равными векторами позволяет решать различные задачи в физике и математике, связанные с перемещением и силами.
Свойства равных векторов
Векторы называются равными, если они имеют одинаковую направленность и длину. Равные векторы обозначаются одинаковыми строчными буквами: а = b.
Свойства равных векторов:
| Свойство | Описание |
|---|---|
| Симметричность | Если векторы а и b равны, то векторы b и а также равны: b = а. |
| Транзитивность | Если векторы а и b равны, и векторы b и c равны, то векторы а и c также равны: а = c. |
| Добавление равных векторов | Если векторы а и b равны, то их сумма равна: а + b = b + a. |
| Умножение равных векторов на число | Если вектор а равен вектору b, то их умножение на число λ также равно: λа = λb. |
Знание этих свойств позволяет упростить решение задач и вычислений, связанных с векторами.
Примеры равных векторов
Векторы могут быть равными, если их длины равны и они имеют одинаковое направление. Ниже приведены примеры равных векторов:
Пример 1:
- Вектор AB = (3, 4)
- Вектор CD = (3, 4)
Векторы AB и CD равны, так как у них одинаковая длина (5) и одинаковое направление.
Пример 2:
- Вектор EF = (-2,

- Вектор GH = (-2,

Векторы EF и GH также равны, так как у них одинаковая длина (8) и одинаковое направление.
Пример 3:
- Вектор IJ = (0, -3)
- Вектор KL = (0, -3)
Векторы IJ и KL равны, так как у них одинаковая длина (3) и они направлены в одном и том же направлении.
В целом, равные векторы имеют одинаковую длину и направление. Они выражают одно и то же перемещение в пространстве.
Отличие равных векторов от коллинеарных векторов
Однако, равные векторы могут иметь разные начальные точки, поэтому их положение в пространстве может быть разным. Хотя эти векторы размещаются по-разному, они все равно считаются равными из-за своих характеристик — направления и значения.
Коллинеарные векторы — это векторы, которые имеют одно и то же направление или противоположное направление. Они могут иметь разные значения, но их направления параллельны друг другу. Коллинеарные векторы не считаются равными, поскольку их значения не совпадают, но они часто используются для описания линейных зависимостей и параллельных переносов в пространстве.
| Вид векторов | Значения | Направление | Равенство |
|---|---|---|---|
| Равные векторы | Одинаковые | Одинаковое | Равны |
| Коллинеарные векторы | Разные | Параллельное | Не равны |
Таким образом, отличие равных векторов от коллинеарных векторов заключается в том, что равные векторы имеют одинаковые значения и направления, а коллинеарные векторы имеют параллельные направления, но разные значения.
Зависимость между равными векторами и переходом к другой системе координат
Однако, при переходе от одной системы координат к другой, векторы могут изменить свои компоненты, но при этом оставаться равными. Это происходит из-за изменения системы координат и способа описания вектора.
Для наглядного представления зависимости между равными векторами и переходом к другой системе координат, можно представить таблицу, где в каждой строке будут представлены компоненты вектора в разных системах координат.
| Вектор | Система координат (x, y, z) | Система координат (x’, y’, z’) |
|---|---|---|
| A | (1, 2, 3) | (4, 5, 6) |
| B | (-1, 0, 2) | (-3, -2, 0) |
Таким образом, вектор A в первой системе координат равен вектору A во второй системе координат, несмотря на различие в значениях их компонент. То же самое справедливо и для вектора B.
Зависимость между равными векторами и переходом к другой системе координат является важным аспектом векторной алгебры и широко применяется в различных областях науки и техники.
Практическое применение равных векторов
Вопрос-ответ:
Что такое вектор?
Вектор — это математический объект, который имеет направление и длину.
Какие вектора называются равными?
Векторы называются равными, если они имеют одинаковое направление и одинаковую длину.
Как определить, равны ли два вектора?
Два вектора считаются равными, если их компоненты (координаты) равны друг другу.
Может ли вектор иметь нулевую длину?
Да, вектор может иметь нулевую длину, в этом случае он называется нулевым вектором.
Что происходит, когда векторы сложив или вычтя, получают другой вектор?
Когда векторы складываются или вычитаются, получается новый вектор, который является суммой или разностью соответствующих компонент исходных векторов.