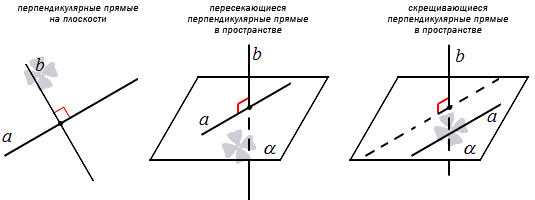
Перпендикулярные прямые — это особый тип прямых, который играет важную роль в геометрии. Они пересекаются друг с другом и образуют прямой угол в точке пересечения. Отличительной особенностью перпендикулярных прямых является то, что их углы равны 90 градусам. Этим свойством они отличаются от других типов прямых, которые могут образовывать углы меньше или больше 90 градусов.
Перпендикулярные прямые имеют множество полезных свойств, которые используются в различных областях, включая архитектуру, инженерию и физику. Одно из самых важных свойств перпендикулярных прямых заключается в том, что они являются оптимальным способом соединения двух точек на плоскости. Поэтому они широко применяются в построении прямоугольных фигур и измерении расстояний между точками.
Примерами перпендикулярных прямых могут служить вертикальная и горизонтальная оси на координатной плоскости. Эти две прямые пересекаются в точке начала координат (0, 0) и образуют прямой угол. Также перпендикулярные прямые можно встретить в строительстве, когда рисуются перпендикулярные линии для правильного соединения элементов конструкции или построения прямого угла для обозначения угла стены или поворота.
Перпендикулярные прямые
Чтобы две прямые были перпендикулярными, они должны отвечать следующему условию: произведение коэффициентов наклона этих прямых должно быть равно -1. Например, если уравнения прямых имеют вид y = mx + b1 и y = nx + b2, то условие перпендикулярности будет выглядеть так: mn = -1.
Перпендикулярные прямые играют важную роль в различных областях науки и техники. Например, в архитектуре они используются при построении прямых стен зданий или складывания деталей строительных конструкций. В математике перпендикулярные прямые помогают решать задачи на построение перпендикуляров, находить углы и определять типы треугольников.
Примеры перпендикулярных прямых можно встретить в повседневной жизни. Например, вертикальные стойки шкафа могут быть перпендикулярными горизонтальным полкам. Другой пример — перпендикулярность нитки вертикальной оси на весах, которая позволяет определить точку равновесия.
Знание свойств и правил перпендикулярных прямых широко используется в различных областях и помогает в решении задач и проблем, связанных с геометрией и пространственными отношениями.
Определение
Основным свойством перпендикулярных прямых является то, что у них никакие участки не совпадают друг с другом. Они всегда пересекаются при угле в 90 градусов, а их наклоны друг к другу всегда противоположны. С другими словами, если одна прямая выглядит «возрастающей» с левого верхнего угла вниз, то вторая прямая будет выглядеть «убывающей» в том же направлении. Это важное свойство перпендикулярных прямых позволяет использовать их во многих областях, таких как геометрия, строительство и инженерия.
Примерами перпендикулярных прямых могут служить оси координат в плоскости, где ось абсцисс и ось ординат образуют прямой угол. Также, стены в зданиях могут быть перпендикулярными друг другу, а также они могут быть использованы в качестве направляющих линий при построении кругов и прямоугольников.
Понимание понятия перпендикулярных прямых является важным для решения задач, связанных с геометрией и строительством, а также в ряде других научных и инженерных областей.
Что такое перпендикулярные прямые
Пересечение перпендикулярных прямых образует четыре прямых угла, каждый из которых равен 90 градусам. Также можно сказать, что они являются взаимно перпендикулярными.
Для двух прямых быть перпендикулярными, их угловой коэффициент должен быть обратным и равным (-1), то есть если одна прямая имеет угловой коэффициент k, то для перпендикулярной прямой угловой коэффициент будет -1/k.
Из свойств перпендикулярных прямых следует, что они не пересекутся в любой точке, кроме точки пересечения. Также, если угловой коэффициент одной прямой равен нулю, то перпендикулярная прямая будет горизонтальной, а если угловой коэффициент равен бесконечности, то перпендикулярная прямая будет вертикальной.
| Пример | Уравнение |
|---|---|
| Прямая А с угловым коэффициентом 2 | y = 2x |
| Перпендикулярная прямая B с угловым коэффициентом -0.5 | y = -0.5x |
Способы определения перпендикулярности
- Способ №1: Геометрическое определение. Перпендикулярные прямые можно определить по их взаимному расположению. Если две прямые пересекаются и при этом образуют прямой угол, то они являются перпендикулярными.
- Способ №2: Сравнение коэффициентов наклона. Коэффициент наклона прямой определяет ее угол наклона относительно оси абсцисс. Если две прямые имеют коэффициенты наклона, являющиеся отрицательно-обратными величинами (то есть при умножении одного на другой получается -1), то они перпендикулярны.
- Способ №3: Использование теоремы Пифагора. Если известны длины сторон прямоугольного треугольника, образуемого двумя прямыми и отрезком, соединяющим их пересечение, то можно применить теорему Пифагора. Если сумма квадратов длин катетов равна квадрату гипотенузы, то прямые являются перпендикулярными.
Каждый из этих способов имеет свои особенности и применяется в различных ситуациях в геометрических задачах для определения перпендикулярности прямых.
Свойства
Перпендикулярные прямые обладают несколькими важными свойствами:
Свойство 1: Перпендикулярные прямые образуют прямой угол друг с другом. Это значит, что угол между ними равен 90 градусов.
Свойство 2: Если две прямые перпендикулярны к одной и той же третьей прямой, то они параллельны между собой. Это свойство называется транзитивностью перпендикулярности.
Свойство 3: Если прямые перпендикулярны между собой, то каждая из них перпендикулярна к любой прямой, лежащей в той же плоскости.
Свойство 4: Если прямая перпендикулярна к одной прямой, и параллельна другой, то эти две прямые параллельны.
Свойство 5: Если две прямые перпендикулярны к третьей, то каждая из них перпендикулярна к плоскости, содержащей эту третью прямую.
Эти свойства помогают в решении задач, связанных с перпендикулярными прямыми и строительством перпендикуляров на плоскости.
Прямые лежат в одной плоскости
Когда говорят, что прямые перпендикулярны, это означает, что они образуют прямой угол. При этом, важно отметить, что перпендикулярные прямые лежат в одной плоскости.
Плоскость определяется двумя перпендикулярными прямыми, которые называются основными. Все остальные прямые, лежащие на этой плоскости, также будут перпендикулярны основным прямым. Это свойство позволяет использовать перпендикулярные прямые для построения различных геометрических фигур, таких как квадраты, прямоугольники и параллелограммы.
Таким образом, понимание того, что перпендикулярные прямые лежат в одной плоскости, является важным элементом в изучении геометрии и помогает решать различные задачи, связанные с перпендикулярными прямыми.
Углы между перпендикулярными прямыми
Перпендикулярные прямые обладают особым свойством, касающимся углов между ними. Угол между перпендикулярными прямыми равен 90 градусам (или четверти полного круга).
Это свойство можно наглядно представить с помощью двух пересекающихся перпендикулярных прямых. Угол, образованный двумя такими прямыми на той же плоскости, всегда будет равен 90 градусам.
Перпендикулярные прямые часто используются в геометрии и строительстве. Они помогают определять и контролировать прямоугольные формы, как, например, в строительстве домов и прокладке мостов.
Углы между перпендикулярными прямыми также имеют важное значение в математике. Они являются основой для определения прямоугольных треугольников и других геометрических фигур.
Вопрос-ответ:
Что такое перпендикулярные прямые?
Перпендикулярные прямые — это две прямые, которые пересекаются и образуют прямой угол.
Какое свойство обладают перпендикулярные прямые?
Одно из главных свойств перпендикулярных прямых — они имеют равные прямые углы при пересечении.
Как можно определить, являются ли две прямые перпендикулярными?
Для проверки перпендикулярности прямых можно использовать два способа: 1) Проверить, что угол между прямыми равен 90 градусам. 2) Проверить, что произведение коэффициентов наклона прямых равно -1.
Можно ли привести примеры перпендикулярных прямых в реальной жизни?
Да, в реальной жизни есть множество примеров перпендикулярных прямых. Например, углы стен домов часто образуют перпендикулярные прямые. Также перпендикулярные прямые можно обнаружить на раскрестках дорог или на сетке в поле.
Какие другие свойства имеют перпендикулярные прямые?
Перпендикулярные прямые также имеют следующие свойства: 1) Угол между перпендикулярными прямыми равен 90 градусам. 2) Произведение коэффициентов наклона равно -1.
Что такое перпендикулярные прямые?
Перпендикулярные прямые — это прямые, которые пересекаются под прямым углом, то есть угол между ними равен 90 градусам. Другими словами, перпендикулярные прямые можно представить, как две прямые, которые идут одна из верхнего угла к другому.