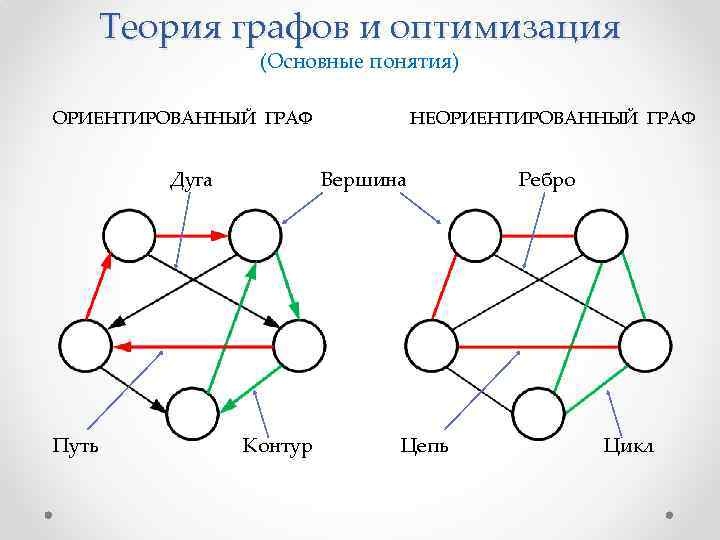
Ориентированный граф — это математическая структура, состоящая из вершин и ребер, где каждое ребро имеет направление и связывает две различные вершины. В ориентированном графе каждое ребро имеет начальную и конечную вершину, а также направление, указывающее на то, какая вершина является начальной, а какая — конечной.
Ориентированные графы широко используются в различных областях, таких как транспортные сети, анализ данных, компьютерные сети и многие другие. Они позволяют моделировать и изучать сложные системы с учетом направления связей между их элементами. Ориентированные графы также являются важным инструментом в теории графов.
Одним из основных понятий в ориентированных графах является путь. Путь в ориентированном графе — это последовательность вершин, такая что каждая пара соседних вершин соединена ребром. Путь может быть направленным от одной вершины к другой или обратно. Существуют различные алгоритмы для поиска пути в ориентированных графах, которые позволяют находить оптимальные маршруты или определить связность графа.
Понятие ориентированного графа
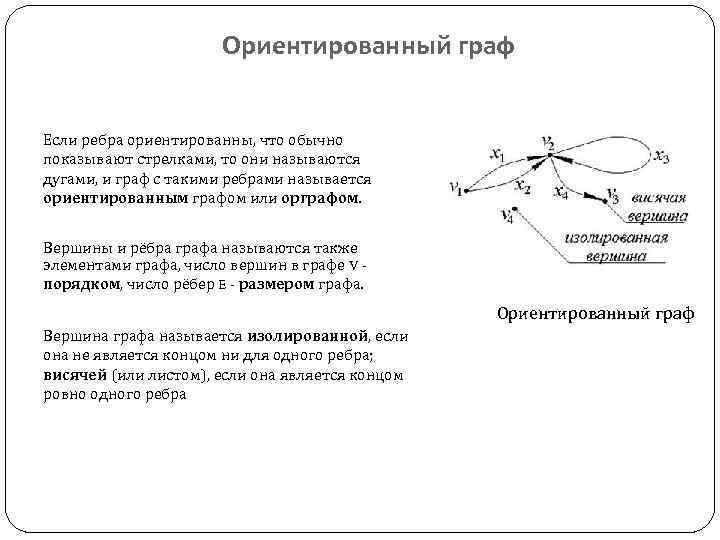
Ориентированный граф представляется с помощью множества вершин, которые могут быть связаны направленными ребрами. Каждое ребро имеет начальную и конечную вершину, определяющие направление связи. Например, если вершина A имеет направленное ребро к вершине B, это означает, что существует отношение или связь, исходящая от A и направленная к B.
Ориентированный граф может использоваться для моделирования различных реальных ситуаций, таких как транспортные сети, социальные сети, графики выполнения программ и т. д. Например, в транспортной сети можно представить станции как вершины, а дороги между станциями как направленные ребра, указывающие направление движения автомобилей.
Ребра и степень вершины
В ориентированном графе ребра обладают своими характеристиками. Направление ребра показывает порядок, в котором вершины связаны. Каждое ребро имеет начальную и конечную вершину, и их порядок определяет направление.
Степень вершины в ориентированном графе — это количество ребер, выходящих из данной вершины или входящих в нее. Она может быть как положительной, так и отрицательной в зависимости от направления связей. Например, у вершины A может быть степень 2, если она имеет два исходящих ребра, и степень -1, если имеет одно входящее ребро.
Особенности ориентированного графа
Ориентированный граф отличается от неориентированного тем, что в нем направление связей имеет значение. Это позволяет более точно моделировать реальные ситуации, в которых важно учитывать направление отношений. В ориентированном графе также возможны петли, когда ребра соединяют вершину с самой собой, и множественные ребра, когда между двумя вершинами существует несколько направленных связей.
Ориентированные графы часто используются в алгоритмах и структурах данных для решения различных задач, таких как поиск пути, топологическая сортировка, обнаружение циклов и другие.
Граф и его свойства
Направленность графов
Граф называется ориентированным, если каждое ребро имеет направление. То есть каждая пара вершин соединяется двумя ребрами, одно в направлении от первой вершины ко второй, и другое в обратном направлении. Ориентированные графы используются для моделирования направленных связей, типичных для таких систем, как транспортные сети или зависимости задач в проектном планировании.
Связность графов
Графы могут быть связными и несвязными. Связный граф — это граф, в котором существует путь между любыми двумя вершинами. Несвязный граф состоит из нескольких связных компонентов, в каждом из которых есть вершины и ребра, но отсутствуют пути между вершинами разных компонентов. Связные графы широко используются для моделирования связей и взаимодействий в различных системах, например, в социальных сетях или транспортных сетях.
Ориентированные циклы
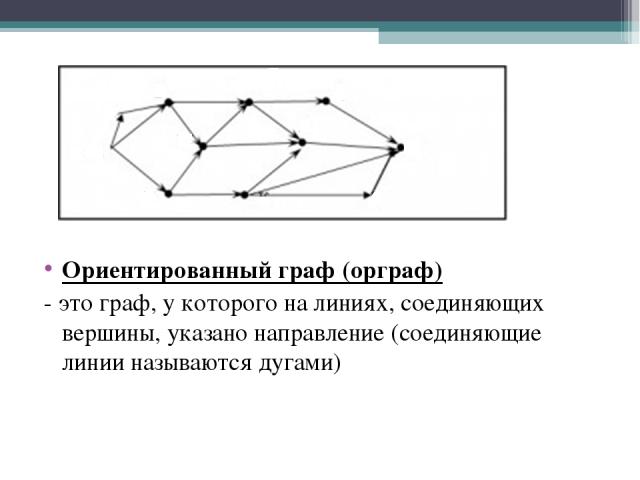
Ориентированный цикл в графе — это последовательность вершин и ребер, начинающаяся и заканчивающаяся в одной и той же вершине, и проходящая по разным вершинам и ребрам графа. Ориентированные циклы могут быть причиной нежелательных эффектов в системах, таких как петли в управлении или зацикливание при обработке данных. Поэтому при анализе графов важно обнаруживать и учитывать наличие циклов.
Веса ребер
Ребра в графе могут иметь веса, которые могут отражать различные характеристики связей между вершинами. Веса ребер могут быть положительными, отражающими стоимость или расстояние, или отрицательными, указывающими на противоположную характеристику. Взвешенные графы используются, например, для поиска кратчайших путей или решения задач коммивояжера.
Ориентация ребер
В ориентированных графах ребра могут иметь различное направление, указывающее на направление связи между вершинами. Направление ребер может быть отражено в алгоритмах обхода графов и использоваться для моделирования разных типов связей. Например, в алгоритмах топологической сортировки ориентация ребер позволяет учесть зависимости задач в проектном планировании.
В данной статье мы рассмотрели лишь некоторые из возможных свойств графов. Графы представляют собой мощный инструмент для анализа и моделирования различных систем и взаимодействий. Понимание основных свойств графов помогает в эффективном использовании их в различных областях деятельности.
Направленность ребер графа
В графе ребра могут быть ориентированными или неориентированными. В случае ориентированных ребер каждое ребро имеет направление, которое определяется начальной и конечной вершинами. Направленное ребро обозначается стрелкой, указывающей на его направление.
Направленные ребра позволяют моделировать взаимосвязь между вершинами, где направление имеет значение. Например, направленные ребра могут использоваться для представления потока информации, передвижения объектов или зависимостей между задачами.
В отличие от ориентированных, неориентированные ребра не имеют направления и представляют просто связь между двумя вершинами без указания направления.
Направленность ребер графа является важным аспектом при анализе и моделировании графовых структур. Она позволяет точнее задать взаимосвязи между вершинами и учитывать направление, что делает граф более гибким и мощным средством для решения различных задач.
Определение ориентированного графа
В ориентированном графе вершины соединяются направленными ребрами, которые образуют пары упорядоченных пар (a, b). Вершина «a» называется начальной вершиной ребра, а вершина «b» — конечной вершиной ребра. Направление ребра указывается от начальной вершины к конечной.
Ориентированный граф может быть представлен в виде матрицы смежности или списка смежности. В матрице смежности, направление ребра отображается номером строки и столбца, где 1 указывает на наличие ребра, а 0 — на его отсутствие. В списке смежности, для каждой вершины указывается список вершин, с которыми она соединена.
Ориентированные графы широко применяются в различных областях, таких как транспортные сети, информационные системы, социальные сети и др. Они позволяют установить направление движения, связи и зависимости между различными элементами системы.
Примеры ориентированных графов
1. Путешествие по городам
Одним из примеров ориентированного графа может служить сеть дорог, по которым можно перемещаться между городами. Путешествие по городам можно представить в виде ориентированного графа, где города представлены вершинами, а дороги между городами — ребрами. Направление движения по дорогам определяется ориентацией графа.
2. Связи в социальных сетях
Ориентированный граф может использоваться для моделирования связей между пользователями в социальных сетях. Вершины графа представляют пользователей, а ориентированные ребра обозначают дружбу или подписку. Направление ребра может указывать на то, кто подписан на кого или кто дружит с кем.
3. Направление информационного потока
Ориентированный граф может быть использован для моделирования направления информационного потока в системе. Например, в компьютерной сети можно представить компьютеры и серверы как вершины графа, и направленные ребра обозначать поток информации между ними.
4. Моделирование зависимостей задач
Ориентированный граф часто применяется для моделирования зависимостей задач в проекте. Вершины графа представляют задачи, а ориентированные ребра определяют зависимости между ними. Направление ребра указывает на то, что одна задача должна быть выполнена перед другой.
Ориентированные графы широко применяются в различных областях, включая транспорт, социальные сети, информационные системы и управление проектами. Они позволяют моделировать сложные взаимосвязи и эффективно анализировать различные сценарии.
Особенности ориентированного графа
Ориентированный граф может быть представлен в виде матрицы смежности или списка смежности. В матрице смежности каждый элемент ячейки i, j указывает на наличие ребра из вершины i к вершине j. В списках смежности для каждой вершины i хранится список вершин, достижимых из вершины i.
Одной из особенностей ориентированного графа является наличие ориентированных циклов. Ориентированный цикл – это замкнутый путь в графе, в котором можно пройти от одной вершины к другой, двигаясь по направлению ориентированных ребер. Наличие циклов в ориентированном графе может быть полезным в некоторых случаях, однако может стать проблемой при выполнении некоторых алгоритмов.
Для работы с ориентированным графом могут использоваться различные алгоритмы, такие как алгоритм поиска в глубину (DFS) и алгоритм поиска в ширину (BFS). Эти алгоритмы позволяют производить обход графа и находить пути между вершинами.
Ориентированный граф может использоваться для моделирования различных задач и является основой для реализации различных алгоритмов поиска, сортировки и топологической сортировки. Также ориентированный граф может быть применен для решения задачи коммивояжера, проблемы кратчайшего пути и других задач.
| Особенности ориентированного графа | |
|---|---|
| Ориентированные ребра | Наличие направления у ребер графа. |
| Ориентированные циклы | Возможность образования замкнутых путей. |
| Матрица смежности | Хранение графа в виде двумерной матрицы. |
| Список смежности | Хранение графа в виде списка вершин. |
| Алгоритмы обхода | DFS и BFS для обхода графа и поиска путей. |
Применение ориентированных графов
Ориентированные графы находят широкое применение в различных областях, где необходимо моделировать и анализировать направленные связи между объектами. Ниже представлены некоторые примеры применения ориентированных графов.
Транспортное планирование
Ориентированные графы используются в транспортном планировании для моделирования и оптимизации потоков транспортных средств. Каждая дорога или маршрут представляется в виде направленного ребра, а узлы графа представляют местоположения. Такая модель позволяет определить наиболее эффективные маршруты, учесть направление движения транспорта и прогнозировать потоки в будущем.
Сетевое планирование
Ориентированные графы широко применяются в сетевом планировании, где необходимо моделировать и анализировать сложные сети связей. Например, графы могут использоваться для решения задач оптимального распределения ресурсов, планирования производственных процессов, управления проектами и других задач. Ребра графа представляют связи между элементами сети, а узлы — сами элементы.
Ориентированные графы также находят применение в биоинформатике, социальных сетях, анализе данных, компьютерной графике и других областях, где важно учитывать направленность связей между объектами. Полученные из ориентированных графов данные позволяют получить новые знания, легче анализировать и планировать различные процессы и структуры, а также предсказывать будущее состояние системы.
Вопрос-ответ:
Что такое ориентированный граф?
Ориентированный граф — это граф, у которого каждое ребро имеет направление, указывающее порядок между вершинами.
Какие примеры ориентированных графов вы можете привести?
Примерами ориентированных графов могут быть: сети передачи данных, дорожные сети с односторонними дорогами, графы зависимостей в программировании и др.
Как можно представить ориентированный граф в виде матрицы смежности?
Ориентированный граф можно представить в виде матрицы смежности, где элемент (i, j) равен 1, если есть направленное ребро из вершины i в вершину j, и 0 в противном случае.
Чем отличается ориентированный граф от неориентированного?
Ориентированный граф имеет направление на каждом ребре, в то время как неориентированный граф не имеет направления на ребрах и каждое ребро рассматривается как двустороннее.
Какими свойствами обладает ориентированный граф?
Ориентированный граф может быть связным или несвязным, ациклическим или содержать циклы, иметь ориентированные пути или быть полностью связанным. В нем также можно рассматривать входящие и исходящие степени вершин.