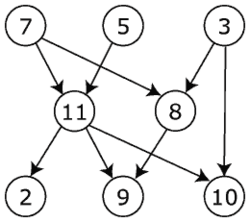
Ориентированный граф — это важная структура данных, которая состоит из вершин и направленных ребер, связывающих эти вершины. Важной особенностью ориентированного графа является то, что направление ребер имеет значение: они указывают на то, в каком направлении можно проходить от одной вершины к другой. Это отличает ориентированный граф от неориентированного графа, где ребра не имеют направления.
Ориентированные графы могут быть использованы в различных областях, таких как компьютерная наука, математика, логистика и многое другое. Например, они могут быть использованы для моделирования сетей связей, где вершины представляют узлы или объекты, а ребра представляют связи или отношения между ними.
Ориентированные графы обладают мощным математическим аппаратом, который позволяет проводить различные анализы. Одним из таких анализов является поиск кратчайшего пути между двумя вершинами. Для этого можно использовать алгоритмы, такие как алгоритм Дейкстры или алгоритм Флойда-Уоршелла.
Ориентированный граф
В ориентированном графе вершины представляют собой объекты, а ребра — связи между ними. Ребра могут быть направленными, то есть двукратные, или однонаправленные. При этом ребра могут быть также взвешенными, то есть иметь определенный вес или стоимость, что позволяет задать значимость связей между вершинами.
Ориентированные графы находят широкое применение в различных областях, таких как компьютерные науки, математика, сетевые технологии и транспортное планирование. Они позволяют моделировать различные процессы, отслеживать связи и взаимодействия между объектами, а также находить оптимальные пути и решать различные задачи оптимизации.
Определение и применение
Ориентированные графы широко применяются в разных областях, таких как транспортные сети, социальные сети, компьютерные сети и другие. Они позволяют моделировать и анализировать различные процессы и взаимосвязи между элементами.
Например, в транспортных сетях ориентированный граф может представлять дорожную сеть, где вершины представляют кроссроады или узлы, а ребра указывают направление движения. Это позволяет оптимизировать маршруты, выявлять пробки или анализировать потоки транспорта.
В социальных сетях ориентированный граф может моделировать связи между пользователями, где вершины представляют пользователей, а ребра указывают направление взаимодействия или отношения. Это помогает анализировать группы связей, прогнозировать влияние или выявлять ключевых пользователей.
Ориентированный граф также применяется в алгоритмах поиска пути, топологической сортировке, анализе взаимосвязей и других областях, где важна учет направления связей между элементами.
В итоге, ориентированный граф играет важную роль в моделировании и анализе сложных систем, обладая широким спектром применений в различных областях.
Что такое ориентированный граф и как он используется в программировании?
Графы являются важным инструментом в программировании и используются в различных задачах, включая:
- Алгоритмы поиска пути: Ориентированные графы могут использоваться для нахождения кратчайшего пути между двумя вершинами. Например, алгоритм Дейкстры использует ориентированные графы для нахождения кратчайшего пути взвешенных графах.
- Системы управления базами данных: Ориентированные графы часто используются для представления связей и зависимостей между данными в базах данных. Это позволяет эффективно запрашивать и анализировать данные.
- Рекурсивные алгоритмы: Ориентированные графы могут использоваться для реализации рекурсивных алгоритмов, таких как обход в глубину и обход в ширину. Эти алгоритмы могут быть полезны, например, для поиска всех возможных путей в графе или для поиска компонент связности.
- Сети и передача данных: Ориентированные графы используются для моделирования сетей и передачи данных. Например, графы могут представлять компьютеры и связи между ними, что позволяет анализировать и оптимизировать работу сети.
- Анализ социальных сетей: Ориентированные графы могут использоваться для анализа социальных сетей, где вершины представляют пользователей, а ребра — их связи и взаимодействия. Это позволяет определять влиятельных пользователей, сообщества и прогнозировать поведение пользователей.
Ориентированные графы предоставляют мощный и гибкий инструмент для моделирования и решения различных задач в программировании. Они позволяют представлять сложные связи и зависимости между данными и анализировать их, что делает их полезными во многих областях, включая алгоритмы, базы данных, сети и социальные сети.
Примеры применения ориентированных графов в различных областях
Транспорт и логистика
Ориентированные графы широко применяются в транспортной и логистической отрасли для планирования и оптимизации маршрутов. Например, они могут использоваться при построении графа дорожной сети для нахождения кратчайшего пути между двумя точками или при моделировании логистических цепочек для определения оптимальных потоков грузов.
Информационные системы
Ориентированные графы широко используются в информационных системах для моделирования и анализа различных процессов. Например, они могут применяться в сетевых топологиях для описания взаимодействия компьютеров и устройств, или в моделировании бизнес-процессов, чтобы определить последовательность шагов и зависимости между ними.
Анализ социальных сетей
Ориентированные графы также нашли применение в анализе социальных сетей. Они используются для изучения взаимосвязей между людьми, группами или организациями. Ориентированные ребра могут помочь определить направление взаимодействия, например, в сетях друзей или в бизнес-сетях, где существуют роли «начальник-подчиненный».
Искусственный интеллект
Ориентированные графы применяются в области искусственного интеллекта для моделирования знаний и решения задач. Например, они могут использоваться для построения логических моделей, где узлы графа представляют концепции, а ребра — отношения между ними. Это может быть полезно для автоматического обучения и принятия решений на основе логических правил.
Биология и генетика
В биологии и генетике ориентированные графы используются для моделирования генетических сетей и взаимодействий между биологическими элементами. Например, они могут помочь определить генетические пути и связи между белками, что позволяет более глубоко изучать жизненный цикл организмов и различные биологические процессы.
Финансы и экономика
В финансовой и экономической сфере ориентированные графы могут быть полезны для моделирования финансовых потоков, прогнозирования рыночных трендов и анализа экономических систем. Например, они могут использоваться для описания зависимостей между компаниями или финансовыми маркетами и определения факторов, влияющих на успешность или неуспешность инвестиций.
Примеры использования ориентированных графов в различных областях являются всего лишь небольшой частью их потенциала. Возможности применения ориентированных графов широки и разнообразны, и их использование продолжает развиваться вместе с развитием новых технологий и методов анализа данных.
Структура графа
Ориентированный граф состоит из вершин и ребер, которые связывают эти вершины между собой. Каждая вершина представляет собой отдельный элемент, а ребро представляет собой связь между двумя вершинами. Ребра могут иметь направление, что делает ориентированный граф различным от неориентированного графа.
Граф представляется в виде набора вершин и набора ребер. Вершины обычно обозначаются числами или буквами, а ребра обозначаются парой вершин, которые они связывают. Для каждой вершины может быть указан список соседних вершин, с которыми она соединена ребром.
Структура графа может быть представлена в виде матрицы смежности или списка смежности. В матрице смежности каждый элемент указывает наличие или отсутствие ребра между двумя вершинами. В списке смежности каждая вершина имеет список своих соседей.
Структура графа позволяет проводить различные операции над ним, такие как поиск пути между вершинами, определение сильно связных компонентов, топологическая сортировка и т. д. Ориентированный граф является важным инструментом в различных областях, таких как компьютерные науки, транспортная логистика, социальные сети и др.
Вершины и ребра: основные элементы ориентированного графа
Первоначально, ориентированный граф создается с определенным набором вершин и пустым набором ребер. Затем, для создания связей между вершинами, добавляются ребра. Каждое ребро указывает на две вершины: начальную и конечную. Ребра образуют направленные связи в графе, показывая, как одна вершина связана с другой.
Вершины могут быть представлены в виде точек или маркеров на графическом изображении графа. Они могут быть обозначены уникальными идентификаторами или именами для удобства обращения к ним. Вершины также могут содержать дополнительную информацию, такую как вес или стоимость связи.
Ребра представляют собой линии или стрелки, соединяющие вершины между собой. Направление стрелки определяется ориентацией ребра. Ребра также могут быть взвешенными, то есть иметь дополнительную информацию о стоимости или длине связи между вершинами.
Ориентированный граф позволяет моделировать и анализировать различные виды зависимостей и взаимосвязей. Например, ориентированный граф может использоваться для моделирования дорожной сети, где вершины представляют города, а ребра — дороги между ними. Такой граф позволяет определить оптимальный маршрут от одного города к другому.
Матрица смежности и список смежности: способы представления ориентированного графа
Ориентированный граф представляет собой совокупность вершин, связанных направленными ребрами или дугами. Для удобства работы с ориентированным графом используются различные способы его представления, такие как матрица смежности и список смежности.
Матрица смежности — это двумерный массив, где строки и столбцы соответствуют вершинам графа. Значение элемента матрицы смежности равно 1, если между соответствующими вершинами существует направленное ребро, и 0, если ребра нет. Таким образом, матрица смежности позволяет хранить информацию о всех ребрах графа. Преимущество матрицы смежности заключается в том, что с ее помощью легко определить наличие ребра между двумя вершинами или получить список соседних вершин для конкретной вершины. Однако, матрица смежности имеет квадратичное время доступа к элементам и занимает большое количество памяти, что может быть непрактично для графов с большим числом вершин.
Список смежности — это массив списков, где индексы массива соответствуют вершинам графа, а элементы списков — соседним вершинам. Таким образом, список смежности позволяет быстро получить список соседей для каждой вершины. Этот способ представления графа экономит память, особенно для разреженных графов, где большинство вершин имеет небольшое количество соседей. Однако, для проверки наличия ребра между двумя вершинами потребуется проход по списку смежности для одной из вершин, что может занять линейное время в худшем случае.
Выбор между матрицей смежности и списком смежности зависит от конкретной задачи и особенностей графа. Если граф плотный и требуется частое определение наличия ребра между вершинами, то лучше использовать матрицу смежности. В случае разреженного графа или задач, где чаще требуется получение списка соседей, список смежности будет более эффективным способом представления графа.
| Вершина 1 | Вершина 2 | Вершина 3 | Вершина 4 | |
| Вершина 1 | 0 | 1 | 0 | 1 |
| Вершина 2 | 1 | 0 | 1 | 0 |
| Вершина 3 | 1 | 0 | 0 | 1 |
| Вершина 4 | 0 | 1 | 0 | 0 |
В приведенной таблице продемонстрирован пример матрицы смежности для ориентированного графа с четырьмя вершинами. Значение 1 в ячейке (i, j) указывает на наличие ребра от вершины i к вершине j, а значение 0 — на отсутствие ребра.
Алгоритмы работы с ориентированными графами
Ориентированный граф может быть использован для решения множества задач, связанных с различными областями. Существует множество алгоритмов, которые позволяют эффективно работать с ориентированными графами и решать задачи на их основе.
Одним из таких алгоритмов является алгоритм обхода графа в глубину (DFS). Он позволяет найти все вершины, достижимые из данной вершины. Алгоритм заключается в посещении вершины и рекурсивном вызове алгоритма для всех ее непосещенных соседей. Таким образом, можно найти компоненты связности в графе, циклы и многое другое.
Другим распространенным алгоритмом работы с ориентированными графами является алгоритм нахождения кратчайшего пути между вершинами, такой как алгоритм Дейкстры или алгоритм Беллмана-Форда. Эти алгоритмы позволяют найти оптимальные пути с учетом весов ребер графа и могут использоваться, например, для поиска кратчайшего пути в сетевых структурах или в GPS-навигации.
Еще одним важным алгоритмом работы с ориентированными графами является алгоритм топологической сортировки. Этот алгоритм позволяет упорядочить вершины графа таким образом, чтобы для каждого ребра (u, v) вершина u предшествовала вершине v. Алгоритм широко применяется, например, в планировании задач или в синтаксическом анализе естественных языков.
Алгоритмы работы с ориентированными графами очень важны в различных областях, таких как транспортное планирование, телекоммуникации, анализ данных и т. д. Они позволяют решать сложные задачи с учетом направленности связей между вершинами и являются неотъемлемой частью современной информатики.
Вопрос-ответ:
Что такое ориентированный граф?
Ориентированный граф — это граф, в котором каждое ребро имеет направление. То есть, если вершины графа обозначают объекты или события, а ребра — связи между ними, то в ориентированном графе ребро представляет собой однонаправленную связь.
Как работает ориентированный граф?
Ориентированный граф работает путем определения направлений связей между вершинами. Каждое ребро в графе имеет указание на направление, и это направление влияет на характер доступа и передачи информации между вершинами. Также, в ориентированном графе возможна проверка наличия или отсутствия пути между вершинами в заданном направлении.
Какие преимущества и недостатки имеет использование ориентированных графов?
Использование ориентированных графов позволяет более точно моделировать реальные ситуации, где имеет значение направление связей между объектами или событиями. Также, ориентированный граф может использоваться для определения пути следования информации или контроля доступа между вершинами. Однако, ориентированный граф может быть сложнее в анализе и обработке по сравнению с неориентированным графом.
Как можно представить ориентированный граф программно?
Ориентированный граф можно представить программно с использованием различных структур данных. Например, можно использовать матрицу смежности, где каждый элемент матрицы указывает на наличие или отсутствие ребра между вершинами. Также, можно использовать списки смежности, где для каждой вершины хранится список ее соседей. В зависимости от задачи и требований, выбор структуры данных может варьироваться.
В каких областях применяются ориентированные графы?
Ориентированные графы широко применяются в различных областях, включая программирование, транспорт, логистику, социологию, биологию и другие. Например, в программировании ориентированный граф может использоваться для представления системы зависимостей между модулями или компонентами программы. В транспорте и логистике он может помочь определить наиболее оптимальный маршрут доставки товаров. В социологии он может использоваться для анализа взаимодействий между людьми в социальных сетях. В биологии он может помочь моделировать взаимодействия между элементами в биологической системе.
Что такое ориентированный граф?
Ориентированный граф — это граф, в котором каждое ребро имеет направление, то есть оно идет из одной вершины в другую.