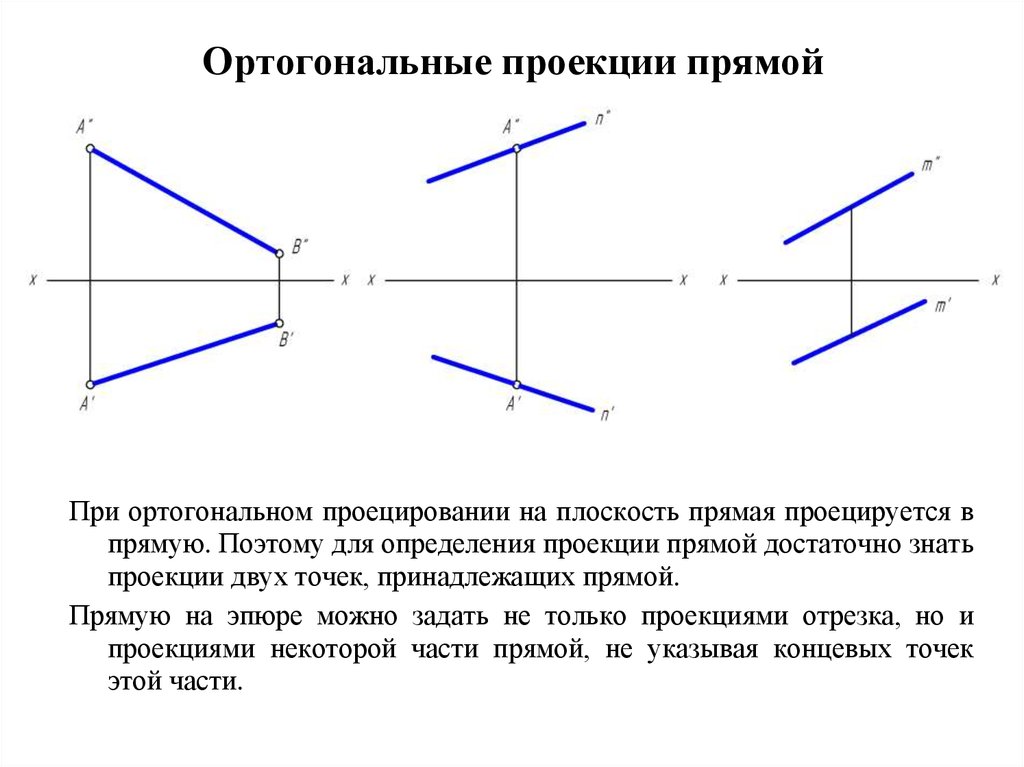
Ортогональное проецирование — это метод представления трехмерных объектов на плоскости с сохранением прямоугольности. Оно широко используется в графическом дизайне, архитектуре, инженерии и других отраслях.
Когда мы проецируем трехмерный объект на фронтальную плоскость, мы получаем двумерное изображение этого объекта, где все прямые и плоскости, параллельные фронтальной плоскости, остаются перпендикулярными ей.
Если примем, что начало координат системы проекций находится на фронтальной плоскости, то прямые, перпендикулярные этой плоскости, будут проходить через него и иметь наклон относительно координатных осей. Такие прямые называются перпендикулярными фронтальной плоскости проекций.
Ортогональное проецирование: определение и основные понятия
При ортогональном проецировании объект проецируется на плоскость перпендикулярно ей. Это значит, что все линии, параллельные этой плоскости, проецируются на нее с сохранением углов и пропорций. Ортогональное проецирование позволяет упростить изображение и обеспечить масштабную точность.
Важным понятием в ортогональном проецировании является фронтальная плоскость проекций. Это плоскость, на которую проецируется объект. Прямая, перпендикулярная этой плоскости, называется проекционной плоскостью. Она служит для построения проекций объекта и определяет направление световых лучей при проецировании.
Еще одним важным понятием является проекционный центр. Это точка, через которую проходят все прямые линии, исходящие от объекта и направленные на проекционную плоскость. Расположение проекционного центра определяет положение проекционной плоскости и может быть любым в пределах пространства.
Ортогональное проецирование можно представить в виде трех проекций объекта – плана (сверху), фасада (спереди) и профиля (сбоку). Все эти проекции вместе дают полное представление о форме и размерах объекта.
Таким образом, ортогональное проецирование является важным инструментом для визуализации объектов в двухмерной форме. Оно позволяет наиболее точно отобразить форму и размеры объекта, сохраняя при этом пропорции и углы.
Ортогональное проецирование: что это такое?
При ортогональном проецировании объекты проецируются на плоскость с помощью перпендикулярных линий, называемых проекционными линиями. Эти линии проходят через точки объекта и пересекают плоскость проекций под прямым углом.
Ортогональное проецирование часто используется в архитектуре, дизайне и инженерии для создания точных и удобочитаемых чертежей. В результате проецирования каждая сторона объекта отображается на плоскости в масштабе и с сохранением пропорций.
Одно из ключевых преимуществ ортогонального проецирования заключается в его точности и предсказуемости результата. Это делает его эффективным средством для визуализации объектов и их измерения. Кроме того, ортогональное проецирование позволяет устранить искажения перспективы, что упрощает восприятие и анализ объектов.
Преимущества ортогонального проецирования:
- Точное отображение размеров и форм объектов
- Предсказуемый результат проецирования
- Устранение искажений перспективы
- Удобочитаемость чертежей и схем
- Широкое применение в архитектуре и инженерии
Ортогональное проецирование является основным инструментом визуализации и представления трехмерных объектов в двумерном виде. Оно широко используется в различных областях, где точность и четкость изображений являются важными критериями.
Фронтальная плоскость проекций: объяснение и свойства
Основное свойство фронтальной плоскости проекций заключается в том, что она перпендикулярна плоскости проекций и параллельна одной из осей системы координат. В зависимости от выбора данной оси, фронтальная плоскость может быть горизонтальной, вертикальной или наклонной.
Фронтальная плоскость проекций является одним из основных инструментов в графическом моделировании и инженерном черчении. Она позволяет создавать двумерные проекции трехмерных объектов с сохранением пропорций и формы.
При использовании фронтальной плоскости проекций важно обратить внимание на выбор оси, которая будет параллельна плоскости проекций. От этого выбора зависят ориентация и видимость объектов на двумерном изображении.
Свойства фронтальной плоскости проекций:
- Перпендикулярность к плоскости проекций;
- Параллельность к одной из осей системы координат;
- Обеспечение сохранения пропорций и формы при проецировании;
- Важность выбора оси, параллельной плоскости проекций, для правильного отображения объектов.
Основные понятия ортогонального проецирования: прямая и плоскость
Прямая проекции — это перенос точки или объекта на плоскость проекций с помощью прямой, перпендикулярной плоскости проекций. Прямые проекции служат для определения положения точек на плоскости и визуализации объектов в двумерной форме.
Перпендикулярная прямая — это прямая, образующая прямой угол с плоскостью проекций. Она проходит через точку объекта, перпендикулярно плоскости проекций и определяет его положение на плоскости проекций.
Плоскость проекций — это фиксированная горизонтальная или вертикальная плоскость, на которую проецируются точки и объекты. Плоскость проекций разделяется на горизонтальную и вертикальную проекцию.
Горизонтальная проекция — это проекция точек и объектов на горизонтальную плоскость проекций. В горизонтальной проекции высота объекта сохраняется, а ширина уменьшается пропорционально масштабу.
Вертикальная проекция — это проекция точек и объектов на вертикальную плоскость проекций. Вертикальная проекция сохраняет ширину объекта, а высота уменьшается пропорционально масштабу.
Использование ортогонального проецирования и понимание основных понятий прямой и плоскости позволяет инженерам и архитекторам создавать точные и понятные чертежи, обеспечивая удобное восприятие и визуализацию объектов.
Перпендикулярная фронтальной плоскости прямая: определение и особенности
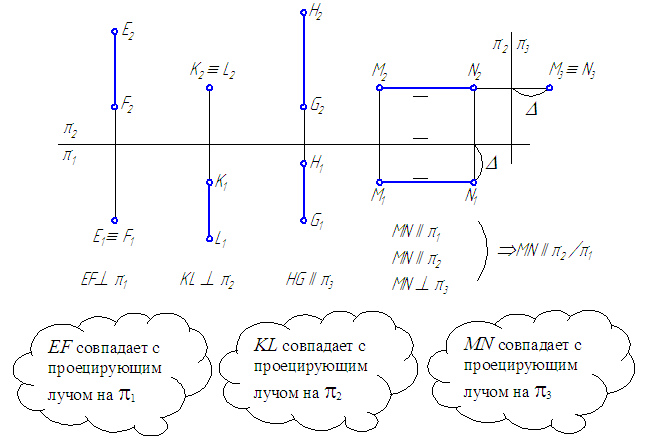
В ортогональном проецировании применяется фронтальная плоскость, которая проходит перпендикулярно к плоскости проекций. Фронтальная плоскость используется для создания проекций объектов на плоскость, а перпендикулярная прямая является результатом проецирования линий и точек объекта на эту плоскость.
Особенность перпендикулярной фронтальной плоскости прямой заключается в том, что она не изменяет своей ориентации при проецировании. Это означает, что длина и направление этой прямой не изменяются при проецировании на плоскость проекций.
Перпендикулярная прямая также служит важным инструментом при создании трехмерных моделей и чертежей. Она позволяет определить взаимное расположение объектов и точек в пространстве, а также помогает визуализировать их в двухмерном представлении.
На практике перпендикулярную фронтальной плоскости прямую можно визуализировать, например, на чертеже здания, где она может служить вспомогательной линией для определения вертикальных элементов или высотных отметок.
В итоге, перпендикулярная фронтальной плоскости прямая играет важную роль в графическом представлении объектов и точек, а также помогает в их анализе и расчете.
Примеры использования перпендикулярной прямой в ортогональном проецировании
Одним из примеров использования перпендикулярной прямой является создание ортографической проекции объекта. Ортографическая проекция позволяет отобразить объект на плоскости с помощью параллельных проекционных линий.
Для создания ортографической проекции используются две перпендикулярные прямые — горизонтальная и вертикальная. Горизонтальная прямая параллельна горизонтальной плоскости проекций, а вертикальная прямая параллельна фронтальной плоскости проекций. Используя эти прямые, можно создать точные чертежи объекта с заданными размерами и пропорциями.
Другим примером использования перпендикулярной прямой в ортогональном проецировании является определение точек пересечения прямых. При создании чертежей и схем часто требуется определить точки пересечения двух или более прямых. Перпендикулярная прямая может использоваться для определения точек пересечения двух прямых на плоскости проекций с помощью перпендикулярной линии, проведенной из точки пересечения на фронтальную плоскость проекций.
| Пример | Описание |
|---|---|
| Пример №1 | На чертеже архитектурного сооружения необходимо определить точку пересечения двух стен. С помощью перпендикулярной прямой можно провести линию из точки пересечения на фронтальную плоскость проекций и точно определить точку пересечения. |
| Пример №2 | При проектировании электрической схемы необходимо определить точку пересечения двух проводов. Перпендикулярная прямая может использоваться для проведения линии из точки пересечения на фронтальную плоскость проекций и точного определения точки пересечения. |
| Пример №3 | При создании чертежа механизма необходимо определить точку пересечения двух деталей. Перпендикулярная прямая может использоваться для проведения линии из точки пересечения на фронтальную плоскость проекций и точного определения точки пересечения. |
Перпендикулярная прямая является важным инструментом в ортогональном проецировании, позволяющим создавать точные и понятные чертежи и схемы. Она используется для создания ортографической проекции объекта, определения точек пересечения прямых и других задач, связанных с ортогональным проецированием.
Понятие проекции прямой на фронтальную плоскость: объяснение и примеры
Проекции прямых на фронтальную плоскость могут быть параллельными, пересекающимися или сливающимися. В случае параллельных проекций, прямая и ее проекция находятся на одном перпендикуляре к фронтальной плоскости. Когда проекции пересекаются, отрезок, представляющий проекцию, будет располагаться между двумя точками, в которых прямая пересекает плоскость. Сливающиеся проекции возникают, когда прямая полностью лежит в фронтальной плоскости.
Пример 1:
Рассмотрим прямую, заданную точками A(1, 2, 3) и B(4, 5, 6). Фронтальная плоскость задана уравнением z = 0. Чтобы найти проекцию этой прямой на фронтальную плоскость, нужно пересечь прямую с плоскостью.
Уравнение прямой можно записать в параметрической форме:
x = 1 + t(4 — 1) = 1 + 3t
y = 2 + t(5 — 2) = 2 + 3t
z = 3 + t(6 — 3) = 3 + 3t
Подставляя z = 0, получаем:
3 + 3t = 0
t = -1
Таким образом, координаты точки пересечения прямой с фронтальной плоскостью будут x = 1 + 3(-1) = -2, y = 2 + 3(-1) = -1, z = 3 + 3(-1) = 0.
Таким образом, проекция прямой АВ на фронтальную плоскость будет отрезком, соединяющим точку А(1, 2, 3) и точку пересечения (-2, -1, 0).
Пример 2:
Рассмотрим прямую, заданную точками C(2, 3, 4) и D(6, 9, 12). Зададим фронтальную плоскость уравнением y = 0. Применим аналогичный подход для нахождения проекции прямой на данную плоскость.
Уравнение прямой:
x = 2 + t(6 — 2) = 2 + 4t
y = 3 + t(9 — 3) = 3 + 6t
z = 4 + t(12 — 4) = 4 + 8t
Подставляя y = 0, получаем:
3 + 6t = 0
t = -0.5
Таким образом, координаты точки пересечения прямой с фронтальной плоскостью будут x = 2 + 4(-0.5) = 0, y = 3 + 6(-0.5) = 0, z = 4 + 8(-0.5) = 0.
Таким образом, проекция прямой CD на фронтальную плоскость будет отрезком, лежащим на оси OX.
Назначение и особенности проекций в ортогональном проецировании
В ортогональном проецировании используются различные типы проекций, которые позволяют отображать объекты с разных точек зрения. Наиболее используемые типы проекций в ортогональном проецировании:
Фронтальная проекция
Фронтальная проекция является одной из основных проекций в ортогональном проецировании. Она используется для отображения объектов, которые находятся перед наблюдателем. В фронтальной проекции все перпендикулярные линии, параллельные оси проекции, изображаются без искажений.
Профильная проекция
Профильная проекция используется для отображения объектов сбоку. В профильной проекции все перпендикулярные линии, параллельные плоскости проекции, изображаются без искажений.
Ортогональное проецирование имеет несколько особенностей:
- Сохранение формы и размеров объектов
- Отсутствие искажений
- Простота и удобство визуализации
Благодаря этим особенностям ортогональное проецирование широко используется в различных областях, где необходимо точно отобразить объекты и сохранить их пропорции.
Связь понятий перпендикулярной прямой и проекции прямой на фронтальную плоскость
При ортогональном проецировании прямая, которая проходит через точку пространства и перпендикулярна фронтальной плоскости, будет проецироваться на эту плоскость в точку. Эта точка является проекцией прямой на фронтальную плоскость. Таким образом, связь между перпендикулярной прямой и проекцией на фронтальную плоскость заключается в том, что перпендикулярная прямая определяет точку проекции на эту плоскость.
Если прямая не перпендикулярна фронтальной плоскости, то ее проекция будет представлять собой отрезок, зависящий от угла, под которым прямая попадает на плоскость. Чем меньше угол между прямой и фронтальной плоскостью, тем длиннее будет проекция прямой.
Пример:
Пусть у нас есть прямая AB, которая имеет точку A в пространстве и перпендикулярна фронтальной плоскости. Согласно принципу ортогонального проецирования, проекция прямой AB на фронтальную плоскость будет точкой P.
| Прямая AB | Проекция P |
|---|---|
| —A——B— | ——-P—— |
Здесь видно, что прямая AB перпендикулярна фронтальной плоскости, и ее проекция на плоскость представляет собой одну точку P.
Вопрос-ответ:
Что такое ортогональное проецирование?
Ортогональное проецирование – это метод представления трехмерных объектов на плоскости с сохранением прямолинейности и параллельности.
Что такое фронтальная плоскость проекций?
Фронтальная плоскость проекций – это плоскость, на которую проецируются объекты при ортогональном проецировании, таким образом, что она параллельна одной из грани объекта.
Что означает «прямая перпендикулярная фронтальной плоскости проекций»?
Прямая перпендикулярная фронтальной плоскости проекций – это прямая, которая проходит через точку на объекте, перпендикулярно фронтальной плоскости проекций.
Каково назначение прямой перпендикулярной фронтальной плоскости проекций?
Прямая перпендикулярная фронтальной плоскости проекций используется для определения глубины объекта при ортогональном проецировании, так как она позволяет построить линии перспективы и определить взаимное расположение различных элементов объекта.
Как называется прямая, перпендикулярная фронтальной плоскости проекций, при ортогональном проецировании?
Прямая, перпендикулярная фронтальной плоскости проекций, называется линией перспективы. Она помогает визуализировать глубину и пространственное расположение объектов при проецировании на плоскость.
Как называется прямая, перпендикулярная фронтальной плоскости проекций при ортогональном проецировании?
Прямая, перпендикулярная фронтальной плоскости проекций при ортогональном проецировании, называется осью проекций.