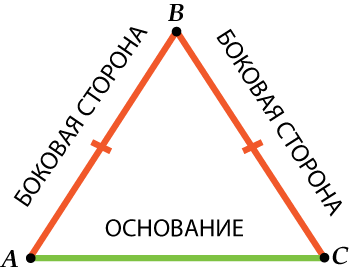
Треугольник — одна из самых простых, но и в то же время интересных геометрических фигур. Его форма представляет собой фигуру с тремя сторонами и тремя углами. Каждая сторона треугольника имеет своё название и играет определенную роль в его структуре и свойствах.
Основой треугольника называют одну из его сторон. Она обычно выбирается в качестве базовой или начальной, относительно которой определяются остальные элементы треугольника. Именно основа задает линию, параллельную которой проводится высота и которая делит треугольник на две равные части.
Высотой треугольника называют отрезок, соединяющий вершину треугольника с его основой, перпендикулярно к основе. Высота является важным элементом треугольника и определяет его площадь. Кроме того, она также служит для нахождения других важных элементов треугольника, таких как биссектрисы.
Биссектрисой треугольника называют линию, которая делит внутренний угол треугольника на две равные части. Она проходит через вершину треугольника и пересекает противолежащую сторону. Биссектрисы имеют большое значение в геометрии и широко применяются при решении различных задач, связанных с треугольниками.
Основа треугольника
Основой треугольника называется одна из его сторон. В треугольнике ABC, основой может быть любая из сторон AB, BC или AC. Основа обычно обозначается буквами a, b или c соответственно.
Знание основы треугольника играет важную роль в геометрии. Например, она определяет величину площади треугольника и позволяет рассчитать многие другие характеристики треугольника.
Для вычисления площади треугольника по формуле S = 0.5 * основа * высота, необходимо знать длину основы и высоту, опущенную на эту основу. Высота треугольника проходит через вершину, противоположную основе, и перпендикулярна к ней.
Основа также используется при вычислении длины биссектрисы треугольника, которая делит эту основу на две части пропорционально длинам прилегающих сторон. Биссектриса проводится из вершины угла, делящего одну из сторон пополам и перпендикулярна к этой стороне.
| Основа | Высота | Биссектриса |
| AB | h | bar{x} |
| BC | h’ | bar{y} |
| AC | h» | bar{z} |
Что такое основа треугольника?
Основа треугольника может быть горизонтальной или вертикальной, в зависимости от его положения. Горизонтальная основа обычно является самой нижней стороной треугольника и расположена на оси x, а вертикальная основа — самой левой или правой стороной треугольника и расположена на оси y.
Знание основы треугольника позволяет определить его площадь с помощью геометрической формулы, которая включает длину основы и высоту треугольника. Кроме того, основа треугольника является одним из условий для определения его биссектрисы — линии, делящей угол треугольника на два равных угла.
| Вид основы треугольника | Примеры | Обозначение |
|---|---|---|
| Горизонтальная основа | Основа треугольника ABC | AB, BC, CA |
| Вертикальная основа | Основа треугольника XYZ | XY, YZ, ZX |
Как найти основу треугольника?
Существует несколько способов найти основу треугольника:
- Если известны длины всех трех сторон треугольника, можно применить формулу для нахождения площади треугольника:
- Если известны длины двух сторон треугольника и угол между ними, можно применить формулу для нахождения площади треугольника:
Пусть a, b и c – длины сторон треугольника, а p – полупериметр треугольника (сумма длин всех сторон, деленная на два). Тогда площадь треугольника S можно найти по формуле:
S = √(p * (p — a) * (p — b) * (p — c))
После нахождения площади треугольника можно применить формулу для нахождения высоты треугольника:
h = (2 * S) / a
Затем основу треугольника можно найти, выбрав сторону, которая лежит на одной прямой с высотой или биссектрисой.
Пусть a и b – длины известных сторон треугольника, а α – угол между этими сторонами. Тогда площадь треугольника S можно найти по формуле:
S = (a * b * sinα) / 2
После нахождения площади треугольника можно применить формулу для нахождения высоты треугольника:
h = (2 * S) / a
Затем основу треугольника можно найти, выбрав сторону, которая лежит на одной прямой с высотой или биссектрисой.
Найдя основу треугольника, можно использовать ее для решения различных задач, связанных с треугольниками, например, для нахождения углов треугольника или для нахождения длины других его сторон.
Высота треугольника
Высота также является самой короткой длиной, соединяющей вершину треугольника с противоположной стороной. Это свойство высоты может быть использовано для нахождения площади треугольника через длину основания и соответствующую высоту.
Высота треугольника является одной из основных характеристик этой геометрической фигуры и играет важную роль в решении различных задач и расчетах, связанных с треугольниками. Высота может быть построена из любой вершины треугольника к противоположной стороне.
Длина высоты может быть найдена с использованием различных способов, в зависимости от доступной информации о треугольнике, как, например, с использованием теоремы Пифагора, теоремы косинусов или прямых измерений. Знание длины высоты может быть полезно при решении задач нахождения площади треугольника, нахождения длин других сторон треугольника или нахождения координат вершин треугольника.
Что такое высота треугольника?
Высота треугольника проходит через одну из его вершин и образует прямой угол с противоположным основанием. Она разделяет треугольник на два прямоугольных треугольника, оба из которых имеют основание, равное основанию исходного треугольника.
Высота треугольника является определающим элементом для вычисления его площади. Площадь треугольника равна произведению длины высоты на половину длины основания. Также высота треугольника позволяет рассчитать его периметр, углы и много других характеристик.
Знание высоты треугольника важно для понимания его свойств и применения в различных сферах, таких как архитектура, инженерное дело и геодезия. Она помогает определить статические и динамические характеристики треугольника, а также решать задачи, связанные с его конструкцией и различными применениями.
Как найти высоту треугольника?
Существует несколько способов найти высоту треугольника:
1. По формуле:
Высоту треугольника можно найти, используя следующую формулу:
h = (2 * S) / a,
где h — высота треугольника, S — площадь треугольника, a — длина основания треугольника.
2. С помощью биссектрисы:
Высоту треугольника также можно определить, используя биссектрису, которая делит основание треугольника на две равные части. Проведите биссектрису из вершины до основания треугольника. Точка пересечения биссектрисы и основания является основанием перпендикуляра к основанию, а высота треугольника — это отрезок, проведенный из вершины до этой точки.
Теперь у вас есть два способа найти высоту треугольника. Выберите наиболее удобный для вас, исходя из имеющихся данных и задачи, которую вы решаете. Помните, что высота треугольника является важной характеристикой и может быть использована для определения других параметров треугольника.
Биссектрисы треугольника
У треугольника каждый из трех углов имеет свою биссектрису. Место пересечения биссектрис называется центром биссектрис. Центр биссектрис треугольника может быть как внутри треугольника, так и на продолжении одной из его сторон.
Центр биссектрис является точкой пересечения всех трех биссектрис треугольника. Он является центром вписанной окружности треугольника.
Интересным свойством биссектрис треугольника является то, что они делят периметр треугольника пропорционально сторонам, противоположным им углам. То есть, если биссектрисы треугольника пересекаются в одной точке, то отношение длины каждой из них к сумме длин двух других равно отношению сторон, противоположных им углам.
Биссектрисы треугольника играют важную роль в геометрии и находят применение в решении различных задач. Они позволяют вычислять площадь треугольника, находить его высоту и многое другое.
| Название | Описание |
|---|---|
| Биссектриса угла | Отрезок, делящий угол на две равные части и сторону, противоположную этому углу, на отрезки, пропорциональные смежным сторонам треугольника. |
| Центр биссектрис | Место пересечения биссектрис треугольника. Может быть как внутри треугольника, так и на продолжении одной из его сторон. |
| Вписанная окружность | Окружность, которая касается всех сторон треугольника внутренним образом и имеет центр в точке пересечения биссектрис треугольника. |
Что такое биссектрисы треугольника?
Биссектриса угла является прямой линией, которая проходит через вершину угла и делит противолежащую сторону на две равные части. Таким образом, биссектрисы треугольника делят каждый из его углов на две равные половины, создавая шесть новых углов.
Биссектрисы треугольника имеют несколько свойств:
- Все биссектрисы треугольника пересекаются в одной точке, известной как центр биссектрис треугольника или центр инкруговой окружности.
- Каждая биссектриса перпендикулярна соответствующей стороне треугольника.
- Каждая биссектриса делит противолежащую сторону треугольника в пропорции, равной отношению длин двух оставшихся сторон.
Использование биссектрис треугольника позволяет решать различные задачи, например, нахождение углов и сторон треугольника, построение вписанных окружностей и много другое.
Вопрос-ответ:
Какие названия могут быть у сторон треугольника?
Строны треугольника могут быть названы любыми маленькими буквами латинского алфавита, например: AB, BC, CA.
Какие названия могут быть у основы треугольника?
Основа треугольника может быть названа любыми двумя буквами из трех, которые обозначают стороны треугольника. Например, если стороны треугольника обозначены как AB, BC и CA, то основа может быть названа AB, BC или CA.
Какие названия могут быть у высоты треугольника?
Высота треугольника может быть названа любой буквой латинского алфавита, обозначающей высоту, например, h. Также высота может быть названа соответствующей буквой основы треугольника, например, если основа треугольника обозначается как AB, то высоту можно обозначить как hAB.
Какие названия могут быть у биссектрисы треугольника?
Биссектриса треугольника может быть названа любой буквой латинского алфавита, обозначающей биссектрису, например, b. Также можно использовать соответствующую букву или буквы основы треугольника, например, если основа треугольника обозначается как AB, то биссектрису можно обозначить как bAB.