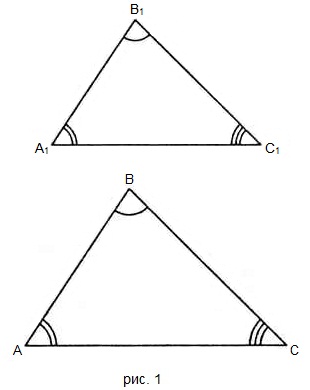
Понятие подобия треугольников является одним из фундаментальных принципов геометрии. Два треугольника называются подобными, если они имеют равные углы и соответствующие стороны пропорциональны. Это важное свойство позволяет строить отношения между треугольниками, а также использовать их для решения различных геометрических задач.
Для того чтобы определить, являются ли два треугольника подобными, необходимо проверить выполнение двух основных принципов. Первый принцип заключается в равенстве углов. Если углы двух треугольников соответственно равны, то треугольники считаются подобными. Определить равенство углов можно с помощью измерительного инструмента или с использованием специальных формул, основанных на свойствах треугольников.
Второй принцип подобия треугольников заключается в пропорциональности соответствующих сторон. Для этого необходимо сравнить отношения длин соответствующих сторон двух треугольников. Если отношения длин сторон равны, то треугольники считаются подобными. Это означает, что один треугольник можно получить из другого путем изменения масштаба без изменения углов.
Основные принципы подобия треугольников
Для того чтобы два треугольника считались подобными, необходимо выполнение следующих принципов:
- Соответствие по сторонам: соответствующие стороны подобных треугольников пропорциональны. Это означает, что соотношение длин сторон одного треугольника к соответствующим сторонам другого треугольника остается постоянным.
- Соответствие по углам: соответствующие углы треугольников считаются равными. Величина каждого угла в одном треугольнике соответствует величине соответствующего угла в другом треугольнике.
Эти принципы являются основными для определения подобия треугольников и позволяют сравнивать и классифицировать их по их геометрическим свойствам.
Определение подобия треугольников
Для того чтобы треугольники считались подобными, необходимо выполнение двух основных критериев:
| 1. | Углы треугольников должны быть равными. Это означает, что соответствующие углы первого и второго треугольников должны иметь одинаковые значения. В случае совпадения углов треугольники называются равными. |
| 2. | Отношение длин сторон должно быть равным. То есть, соответствующие стороны первого и второго треугольника должны иметь одинаковые пропорции. Для этого можно использовать такие характеристики, как отношение длин сторон, отношение площадей или отношение периметров треугольников. |
Если оба критерия выполнены, то мы можем утверждать, что два треугольника подобны. Подобие треугольников является основой для решения множества геометрических задач, связанных с подсчетом расстояний, площадей, объемов и других характеристик фигур.
Понятие подобия треугольников
Для формального определения подобия треугольников существует несколько условий:
- Углы каждого треугольника должны быть равны соответствующим углам другого треугольника. То есть, если угол А1 в первом треугольнике равен углу А2 во втором треугольнике, то угол В1 в первом треугольнике должен быть равен углу В2 во втором треугольнике и т.д.
- Соответствующие стороны каждого треугольника должны быть пропорциональны. Если сторона А1В1 в первом треугольнике пропорциональна стороне А2В2 во втором треугольнике, то сторона В1С1 в первом треугольнике должна быть пропорциональна стороне В2С2 во втором треугольнике и т.д.
Понятие подобия треугольников имеет много практических применений. Оно используется в расчетах и построениях, например, при решении задач по геометрии, в архитектуре, в картографии и других областях, где требуется пропорциональное изменение размеров.
Подобные треугольники являются сходными, но не обязательно равными. Они имеют одни и те же формы, но могут отличаться размерами. При этом отношение длин сторон и отношение площадей подобных треугольников будет одинаковым.
Для лучшего понимания концепции подобия треугольников можно использовать таблицу, в которой приводятся примеры подобных и не подобных треугольников. В этой таблице можно сравнить длины сторон и соответствующие углы для каждого треугольника.
| Пример треугольников | Условие подобия | Подобны ли треугольники? |
|---|---|---|
| Треугольник А1В1С1 со сторонами 3, 4 и 5 | Треугольник А2В2С2 со сторонами 6, 8 и 10 | Да, треугольники подобны, так как углы и стороны пропорциональны |
| Треугольник А1В1С1 со сторонами 3, 4 и 5 | Треугольник А2В2С2 со сторонами 4, 5 и 6 | Нет, треугольники не подобны, так как стороны не пропорциональны |
Понимание подобия треугольников является важным элементом в геометрии и фигурах. Оно позволяет сравнивать и анализировать треугольники на основе их углов и сторон, а также применять полученные знания в практических задачах.
Условия для подобия треугольников
Два треугольника считаются подобными, если выполняются следующие условия:
| Условие | Описание |
| 1. Кратность всех сторон | Длины сторон одного треугольника должны быть пропорциональны длинам сторон другого треугольника с одинаковым коэффициентом пропорциональности. |
| 2. Кратность всех углов | Величины всех углов одного треугольника должны быть равны соответствующим углам другого треугольника. |
Подобные треугольники имеют одинаковую форму, но могут отличаться в размерах. Понимание этих условий позволяет находить подобные треугольники и использовать их свойства в геометрических задачах.
Критерии подобия треугольников
Второй критерий подобия треугольников заключается в том, что их стороны должны быть пропорциональны. Если отношение длины сторон треугольника А к длине сторон треугольника В равно определенному числу, то треугольники А и В считаются подобными.
Эти два критерия позволяют легко определить, являются ли треугольники подобными. Зная значения углов и длин сторон, можно проверить, соответствует ли каждый из критериев. Если оба критерия выполняются, то треугольники подобны и их формы и размеры подобны друг другу.
Критерий собственной подобности
Основные принципы собственной подобности двух треугольников включают соответствие и равенство соответствующих сторон и углов. Когда все стороны одного треугольника пропорциональны соответствующим сторонам другого треугольника, а углы между этими сторонами равны, то треугольники считаются подобными.
Однако в некоторых случаях теорема собственной подобности может быть использована для определения подобности треугольников без полного соответствия и равентсва всех сторон и углов. Этот случай называется критерием собственной подобности.
Критерий собственной подобности треугольников утверждает, что если три угла одного треугольника соответственно равны трём углам другого треугольника, то треугольники считаются подобными.
| Условие подобия | Критерий собственной подобности |
|---|---|
| Все стороны в пропорции | Все углы равны |
Критерий собственной подобности обладает важным свойством: если у треугольников равны два угла, то третий угол автоматически равен. Это свойство позволяет применять критерий собственной подобности для определения подобия треугольников в более простых случаях.
Критерий подобия треугольников по сторонам
Для того чтобы два треугольника считались подобными, необходимо, чтобы их стороны были пропорциональны.
Критерий подобия треугольников по сторонам можно записать следующим образом:
| Условие | |
|---|---|
| OT/OX = PT/PX | Tреугольники ∆OTP и ∆OXP подобны |
| PT/PX = QT/QX | Tреугольники ∆PTO и ∆QXO подобны |
| OT/OX = QT/QX | Tреугольники ∆OTQ и ∆OXQ подобны |
Таким образом, если соблюдаются хотя бы одно из этих условий, треугольники можно считать подобными.
Вопрос-ответ:
Какие два треугольника считаются подобными?
Два треугольника считаются подобными, если соответствующие углы этих треугольников равны, а соотношение длин их сторон также равно.
Какие основные принципы подобия треугольников?
Основные принципы подобия треугольников заключаются в равенстве соответствующих углов и пропорциональности длин соответствующих сторон.
Каким образом можно определить подобие треугольников?
Подобие треугольников можно определить с помощью проверки равенства соответствующих углов и сравнения пропорциональности длин их сторон.
Какие свойства подобных треугольников могут быть использованы для вычислений?
С помощью свойств подобных треугольников можно вычислять отношения длин сторон, площадей и высот, а также находить подобные отрезки и углы.
Какое значение имеет подобие треугольников в геометрии?
Подобие треугольников является одной из основных концепций геометрии, оно используется для решения задач, построения и анализа геометрических фигур.
Какие два треугольника считаются подобными?
Два треугольника считаются подобными, если у них углы равны и их стороны пропорциональны.