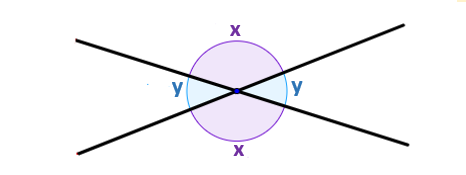
Вертикальные углы – это один из базовых понятий геометрии, которые широко использованы в математике и физике. Они представляют собой два угла, расположенные по разные стороны от пересекающихся прямых или плоскостей, и имеют одинаковую величину. Таким образом, вертикальные углы всегда равны между собой и получаются в результате пересечения прямых под прямым углом.
Главной особенностью вертикальных углов является их равенство друг другу. Другими словами, если мы имеем два вертикальных угла, то мы можем сказать, что они равны. Это свойство можно использовать для решения различных задач и доказательств геометрических теорем.
Например, если у нас есть две прямые, пересекающиеся между собой, и мы знаем, что одна из пар вертикальных углов равна 30 градусам, то мы можем с уверенностью сказать, что вторая пара вертикальных углов также будет равна 30 градусам. Это позволяет нам более эффективно и точно решать геометрические задачи.
Понятие вертикальных углов
Свойства вертикальных углов:
- Вертикальные углы равны: если две прямые пересекаются, то углы, образованные этим пересечением, равны между собой. Это значит, что если один из вертикальных углов имеет меру 60 градусов, то все вертикальные углы, образованные этим пересечением, также будут иметь меру 60 градусов.
- Сумма вертикальных углов равна 180 градусам: если две прямые пересекаются, то сумма мер всех вертикальных углов, образованных этим пересечением, будет равняться 180 градусам. Например, если один из вертикальных углов имеет меру 60 градусов, то другой вертикальный угол, образованный тем же пересечением, будет иметь меру 120 градусов.
Знание свойств вертикальных углов позволяет решать различные геометрические задачи, в том числе находить неизвестные углы или прямые.
Определение и основные характеристики
Основные характеристики вертикальных углов:
- Вертикальные углы всегда равны друг другу. Если две прямые пересекаются, то соответствующие вертикальные углы всегда равны между собой.
- Углы, которые лежат на прямых вертикальных углах, называются вертикальными углами. Например, если две прямые AB и CD пересекаются в точке P, то углы APD и BPC будут вертикальными углами.
- Если сумма двух углов составляет 180 градусов, то эти углы называются смежными. Вертикальные углы являются смежными углами, так как сумма между ними составляет 180 градусов.
- Вертикальные углы часто используются при решении геометрических задач, а также в арифметических и алгебраических вычислениях.
Знание свойств и особенностей вертикальных углов позволяет нам более эффективно анализировать геометрические фигуры и решать различные задачи. Вертикальные углы являются важным элементом в изучении геометрии и имеют широкий спектр применений в практических задачах.
Основные свойства вертикальных углов
1. Вертикальные углы равны. Это означает, что если две прямые пересекаются, то углы, образованные ими, будут равны между собой. Например, если угол 1 равен 60 градусам, то угол 2, который является вертикальным углом к углу 1, тоже будет равен 60 градусам.
2. Вертикальные углы суммируются до 180 градусов. Если мы возьмем два вертикальных угла, то их сумма будет равна 180 градусам. Например, если угол 1 равен 60 градусам, то угол 2, который является вертикальным углом к углу 1, будет равен 120 градусам (180 — 60 = 120).
3. Вертикальные углы могут быть соответствующими. Если две прямые пересекаются и образуют вертикальные углы, то углы, лежащие на одной стороне плоскости и на разных прямых, называются соответствующими. Например, угол 1 и угол 3 – соответствующие углы, так как они лежат на разных прямых и находятся с одной стороны плоскости.
Вертикальные углы широко используются в геометрии и могут быть полезными при решении различных задач.
Как рассчитать вертикальные углы
Первое свойство вертикальных углов заключается в их равенстве. Если две прямые линии пересекаются, то соответствующие вертикальные углы будут иметь одинаковую величину. Это означает, что если один вертикальный угол равен 30 градусам, то и все другие вертикальные углы, возникшие из пересечения этих линий, также будут равны 30 градусам.
Второе свойство вертикальных углов связано с их суммой. Если две прямые линии пересекаются и образуют вертикальные углы A и B, то сумма этих углов всегда будет равна 180 градусам. То есть A + B = 180°. Это свойство можно использовать для расчета величины одного из вертикальных углов, если известна величина другого.
Чтобы рассчитать вертикальные углы, нужно знать их свойства и выполнять элементарные математические действия. Например, если известна величина одного вертикального угла, можно легко рассчитать величину остальных, применяя первое свойство – равенство вертикальных углов.
Также при решении задач по геометрии можно использовать второе свойство вертикальных углов – их сумма, равная 180 градусам. Если известна величина одного вертикального угла и требуется рассчитать другой, можно воспользоваться формулой A + B = 180° для нахождения недостающей величины.
Итак, рассчитать вертикальные углы довольно просто, если у вас есть информация о их свойствах и известны значения других углов или величины линий, пересекающихся.
Методы расчета
Для определения вертикальных углов в градусах необходимо измерить угол между вертикальной линией и линией, задающей угол на плоскости. Затем можно использовать простую формулу для расчета: угол в градусах равен арктангенту от отношения противоположной стороны к прилежащей стороне треугольника. Таким образом, можно найти значение угла в градусах.
Другим методом расчета вертикальных углов является использование углов в радианах. Радиан является единицей измерения угла, определяемой отношением длины дуги окружности к ее радиусу. Для расчета вертикального угла в радианах необходимо умножить значение угла в градусах на константу, равную π (пи) и разделить на 180. Таким образом, можно получить значение угла в радианах.
Выбор метода расчета вертикальных углов зависит от удобства и специфики конкретной ситуации.
Расчет вертикальных углов в геометрии
Свойство 1: Вертикальные углы равны между собой. Если две прямые пересекаются, то все вертикальные углы на этих прямых будут иметь одинаковую меру.
Пример: Пусть имеются две пересекающиеся прямые AB и CD. Угол 1 и угол 2, которые расположены на одной стороне пересечения, будут вертикальными углами и, следовательно, будут равными между собой.
Свойство 2: Сумма вертикальных углов равна 180 градусов. Если имеются две прямые, пересекающие друг друга, то сумма мер всех вертикальных углов, образованных этим пересечением, будет равна 180 градусам.
Пример: Пусть имеются две пересекающиеся прямые EF и GH. Угол 3 и угол 4 будут вертикальными углами. Согласно свойству 2, сумма мер этих углов будет равна 180 градусов.
Знание свойств вертикальных углов позволяет упростить решение задач и нахождение неизвестных углов при пересечении прямых. Они также находят применение при решении задач на построение.
Применение вертикальных углов
Вертикальные углы широко применяются в геометрии и физике для решения задач, связанных с измерением и вычислением углов, а также для анализа пространственных форм и расположения объектов.
Одно из основных свойств вертикальных углов заключается в том, что они равны друг другу. Это означает, что если две прямые пересекаются, образуя четыре угла, а один из этих углов является вертикальным, то два других угла, соседствующих с вертикальным углом, также будут равны между собой.
Применение данного свойства позволяет упростить решение задач, связанных с измерением углов. Например, при измерении угла между вертикальными сторонами здания можно использовать другой, уже известный, вертикальный угол, чтобы найти значение неизвестного угла.
Вертикальные углы также используются при решении пространственных задач. Например, при построении трехмерных моделей нужно учитывать вертикальные углы, чтобы корректно определить расположение объектов в пространстве.
Важно отметить, что вертикальные углы имеют связь с другими типами углов, такими как параллельные углы, вертикальная сумма углов и т. д. Понимание этих связей позволяет углубить знания в геометрии и применять их в решении различных задач.
Вертикальные углы являются важным и полезным концептом в геометрии и физике. Их свойства позволяют упростить решение задач и анализ пространственных форм, а также облегчают измерение и вычисление углов.
Вертикальные углы в архитектуре
Вертикальные углы играют важную роль в архитектуре. Они описывают сочетание различных элементов здания, образуя привлекательные и эстетически приятные композиции.
Вертикальные углы могут быть использованы для создания различных эффектов в архитектуре. Например, они могут подчеркивать вертикальность и статичность здания, создавая впечатление надежности и солидности. Такой подход используется, например, при проектировании небоскребов или храмов.
Вертикальные углы также могут служить для разделения здания на отдельные части или зоны. Они могут являться границей между различными функциональными блоками здания, такими как жилые и коммерческие помещения, или между разными этажами. Это помогает обозначить структуру здания и облегчает его навигацию для посетителей.
Однако, вертикальные углы не всегда должны быть прямыми и глубокими. Они могут быть также закругленными или скругленными, что создает мягкий и более органичный облик здания. Такие углы часто используются в современной архитектуре, чтобы придать зданию более легкое и динамичное выражение.
Независимо от формы и стиля, вертикальные углы играют существенную роль в создании архитектурной композиции. Они помогают определить общий ритм и пропорции здания, придают ему характер и индивидуальность. Использование вертикальных углов требует навыков и творческого подхода к проектированию, чтобы достичь желаемого эффекта и создать впечатление красоты и гармонии.
Использование вертикальных углов в дизайне интерьера
Один из способов использования вертикальных углов в дизайне интерьера — это разделение пространства на зоны или функциональные области. Например, можно использовать вертикальные углы, чтобы создать раздельные зоны для кухни и гостиной в студии, или разделить спальные места в открытой планировке.
Другой способ использования вертикальных углов — это создание визуальной высоты и объема в комнате. Здесь можно использовать вертикальные элементы, такие как полки, шкафы или книжные полки, чтобы привлечь взгляд и создать ощущение пространства.
Для создания эффекта динамичности и движения в дизайне интерьера также можно использовать вертикальные углы. Например, размещение полосатых обоев или прямых линий на стенах или полах может придать комнате оригинальность и энергию.
Обратите внимание, что использование вертикальных углов в дизайне интерьера требует сбалансированного подхода. Слишком большое использование вертикальных элементов может создать ощущение тесноты, а недостаток углов может привести к чувству неопределенности и хаоса.
Итак, при выборе и размещении вертикальных элементов в дизайне интерьера, необходимо учитывать баланс, пропорции и функциональность, чтобы создать гармоничное и приятное пространство.
Вопрос-ответ:
Что такое вертикальные углы?
Вертикальные углы — это пара углов, которые имеют общую сторону и стороны этих углов являются продолжениями друг друга. Одна пара вертикальных углов образуется при пересечении двух прямых линий.
Каково значение вертикальных углов в градусах?
Значение вертикальных углов в градусах равно 180 градусов.
Можно ли вертикальные углы измерить в радианах?
Да, вертикальные углы можно измерять в радианах. 180 градусов соответствует числу pi (пи) в радианах.
Какие примеры вертикальных углов можно привести?
Примером вертикальных углов может быть пересечение двух перпендикулярных прямых. В данном случае вертикальные углы будут образованы четырьмя равными углами, каждый из которых равен 90 градусам.