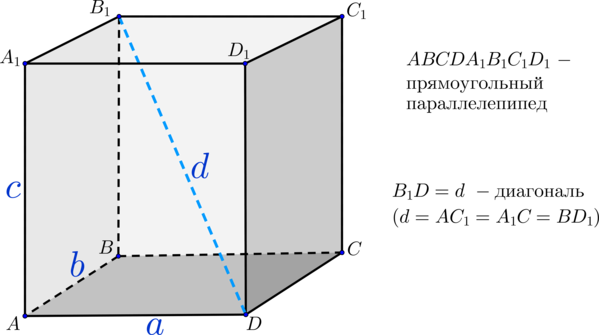
Параллелепипед — одна из основных геометрических фигур, имеющая прямоугольную форму. Его название происходит от греческого слова «пαραλληλεπίπεδον», что означает «имеющий параллельные стороны».
Прямоугольный параллелепипед обладает определенными свойствами, которые делают его уникальным. Для начала, все его грани являются прямоугольниками, а противоположные грани параллельны друг другу.
Важно отметить, что у прямоугольного параллелепипеда все три измерения — длина, ширина и высота — являются различными и формируют прямые углы между собой. Это делает его особенно подходящим для множества практических целей, от строительства и архитектуры до геометрии и математики.
Определение прямоугольного параллелепипеда
Для того чтобы параллелепипед считался прямоугольным, необходимо выполнение определенных свойств:
- Все грани параллелепипеда должны быть прямоугольными;
- Все противоположные грани параллелепипеда должны быть равными по площади и форме;
- Все углы параллелепипеда должны быть прямыми;
- Ребра параллелепипеда должны пересекаться под прямым углом.
Прямоугольный параллелепипед широко используется в геометрии, инженерии, строительстве и других областях. Он является основным элементом для расчетов объемов, площадей и других величин, связанных с трехмерным пространством.
Общая информация о прямоугольном параллелепипеде
1. Форма:
Прямоугольный параллелепипед имеет форму прямоугольника, то есть его грани представляют собой прямоугольники.
2. Ребра и углы:
У прямоугольного параллелепипеда все ребра имеют одинаковую длину, а все углы равны 90 градусов.
3. Грани:
Прямоугольный параллелепипед имеет шесть граней, из которых каждая пара противоположных граней параллельна друг другу.
4. Объем и площадь поверхности:
Объем прямоугольного параллелепипеда равен произведению длины, ширины и высоты, а площадь его поверхности равна сумме площадей всех шести граней.
5. Примеры использования:
Прямоугольные параллелепипеды широко применяются в архитектуре, строительстве, графике и других областях. Они используются для создания зданий, мебели, упаковок и прочих объектов.
Что такое параллелепипед?
Параллелепипед может быть прямоугольным или наклонным. Прямоугольный параллелепипед — это особый тип параллелепипеда, у которого все углы прямые и все грани являются прямоугольниками.
Прямоугольный параллелепипед обладает рядом полезных свойств. У него шесть граней, двенадцать ребер и восемь вершин. Объем прямоугольного параллелепипеда вычисляется как произведение его трех размеров. Площадь поверхности прямоугольного параллелепипеда равна сумме площадей всех его граней.
Параллелепипеды широко применяются в геометрии, физике, архитектуре, строительстве и во многих других областях. Они служат основой для построения и анализа различных пространственных форм, моделей и конструкций.
Понятие прямоугольности
| 1. | Все грани параллелепипеда являются прямоугольниками. |
| 2. | Каждая из граней параллелепипеда перпендикулярна к двум соседним граням. |
| 3. | Все ребра параллелепипеда имеют одинаковую длину. |
Если параллелепипед обладает этими свойствами, то он считается прямоугольным. Прямоугольный параллелепипед является одним из специальных случаев параллелепипеда, когда все его углы являются прямыми. Такие параллелепипеды имеют множество практических применений, включая архитектуру, инженерное дело и геометрическое моделирование.
Свойства прямоугольного параллелепипеда
- У параллелепипеда есть три пары равных противоположных граней. Таким образом, можно провести основание и высоту, соединяющую противоположные грани.
- Углы между гранями параллелепипеда равны 90 градусов. Из-за этого, все грани пересекаются под прямым углом.
- Длины всех ребер параллелепипеда могут быть разными, но для прямоугольного параллелепипеда различаются всего два значения.
- Объем прямоугольного параллелепипеда вычисляется как произведение длины, ширины и высоты.
- Площадь поверхности прямоугольного параллелепипеда равна сумме площадей всех его граней.
Из-за этих свойств прямоугольный параллелепипед используется в ряде сфер, включая геометрию, физику, архитектуру и инженерные приложения.
Три равных пары сторон
Такое свойство делает прямоугольный параллелепипед особенно устойчивым и удобным в использовании. Благодаря равным сторонам, его грани оказываются равными и прямоугольными, что обеспечивает устойчивость в различных позициях и позволяет легко манипулировать объектом.
Кроме того, наличие трех равных пар сторон делает прямоугольный параллелепипед симметричным. Это означает, что его грани и вершины расположены в соответствии с определенными законами симметрии, что придает ему эстетическую привлекательность и гармоничный внешний вид.
Важно отметить, что равные пары сторон прямоугольного параллелепипеда могут быть различными по длине, но в пределах каждой пары сторон имеют одинаковые значения. Также следует учесть, что наличие трех равных пар сторон является необходимым, но не достаточным условием для определения прямоугольного параллелепипеда. Для полного определения параллелепипеда требуется учитывать и другие его свойства.
Прямые углы
Прямые углы образуются пересечением двух взаимно перпендикулярных прямых. В прямоугольном параллелепипеде каждый угол между соединяющими ребрами параллелепипеда является прямым углом. Такие углы встречаются на всех вершинах параллелепипеда и в углах между его гранями.
Прямые углы играют особую роль в единой геометрии. Они позволяют определить множество свойств и особенностей прямоугольного параллелепипеда, таких как его объем, площади граней, диагонали и другие.
Параллельность противоположных граней
Для наглядной иллюстрации этого свойства можно использовать таблицу:
| Противоположная грань | Стороны |
|---|---|
| Первая грань | ABCD |
| Вторая грань | EFGH |
| Третья грань | AEFB |
| Четвертая грань | BCHG |
| Пятая грань | DEHG |
| Шестая грань | ABCD |
Из таблицы видно, что стороны противоположных граней параллелепипеда имеют одинаковое направление и не пересекаются. Это свойство является важным при определении формы и размеров параллелепипеда, а также при решении различных геометрических задач, связанных с ним.
Вопрос-ответ:
Что такое параллелепипед?
Параллелепипед — это геометрическое тело, у которого все грани являются прямоугольниками.
Чем отличается прямоугольный параллелепипед от обычного?
Прямоугольный параллелепипед — это параллелепипед, у которого все грани являются прямоугольниками и углы между этими гранями прямые.
Какие свойства имеет прямоугольный параллелепипед?
Прямоугольный параллелепипед имеет следующие свойства: все его грани являются прямоугольниками, все противоположные грани равны и параллельны друг другу, все углы между гранями прямые.
Как найти объем прямоугольного параллелепипеда?
Объем прямоугольного параллелепипеда можно найти по формуле: V = a * b * c, где a, b и c — длины его сторон.
Можете привести примеры объектов, которые можно сравнить с прямоугольным параллелепипедом?
Некоторые примеры объектов, похожих на прямоугольные параллелепипеды, могут включать в себя подводные лодки, книги, кубические коробки и др.
Что такое параллелепипед?
Параллелепипед — это геометрическое тело, у которого все грани являются прямоугольниками.