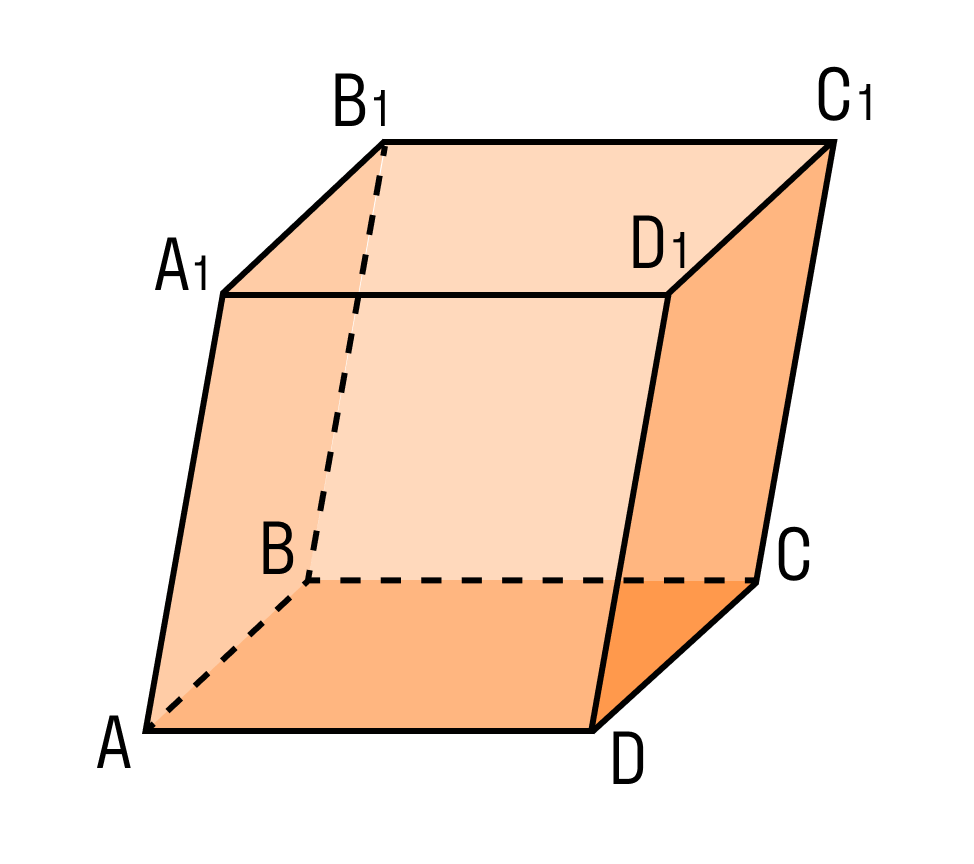
Параллелепипед – это геометрическое тело, которое обладает уникальными свойствами и формой. Среди множества видов параллелепипедов выделяется один особый тип – прямоугольный параллелепипед. Что именно делает его таким уникальным?
Основная отличительная черта прямоугольного параллелепипеда заключается в его форме. Тело состоит из шести граней, каждая из которых является прямоугольником. Именно благодаря этой особенности его и называют прямоугольным. Такое соответствие формы позволяет использовать параллелепипед в различных областях – от геометрии до архитектуры.
Прямоугольный параллелепипед обладает не только уникальной формой, но и рядом других свойств, которые делают его таким популярным. Во-первых, этот вид параллелепипеда имеет три оси: а, b и с, которые пересекаются перпендикулярно и образуют углы в 90 градусов. Во-вторых, все его грани, ребра и углы равны между собой, что делает его симметричным и удобным в использовании.
Что такое прямоугольный параллелепипед?
1. Форма. Все его грани являются прямоугольниками, а все углы этого параллелепипеда прямые, то есть равны 90 градусам.
2. Размеры. У прямоугольного параллелепипеда три пары сторон, каждая из которых параллельна другой, имеют равные величины между собой. Эти размеры называются ширина, длина и высота параллелепипеда.
3. Взаимосвязь сторон. В прямоугольном параллелепипеде длина ребра является общей мерой длин всех трех размеров, то есть периметр прямоугольника, образованного его гранями, равен сумме периметров каждой из трех граней.
4. Объем. Объем прямоугольного параллелепипеда определяется как произведение его ширины, длины и высоты. Таким образом, объем параллелепипеда равен V = Ш х Д х В.
| Свойства прямоугольного параллелепипеда: |
|---|
| Все грани являются прямоугольниками |
| Все углы являются прямыми (равны 90 градусам) |
| Три пары сторон, каждая из которых параллельна другой, имеют равные величины |
| Длина ребра является общей мерой длин всех трех размеров |
| Объем параллелепипеда равен V = Ш х Д х В |
Особенности формы прямоугольного параллелепипеда
- Все грани параллелепипеда являются прямоугольниками, с противоположными сторонами, параллельными друг другу.
- У прямоугольного параллелепипеда шесть граней, которые ограничивают его объем.
- У прямоугольного параллелепипеда все углы прямые, то есть равны 90 градусам.
- Если все его ребра одинаковой длины, параллелепипед становится кубом.
- Прямоугольный параллелепипед может иметь различные размеры длины, ширины и высоты.
Эти особенности делают прямоугольный параллелепипед удобным для использования в различных областях. Например, такие геометрические фигуры широко применяются в строительстве и дизайне для создания объектов, как, например, жилых и коммерческих зданий, мебели и упаковки.
Правильные прямоугольные углы
Правильные прямоугольные углы являются ключевым элементом прямоугольного параллелепипеда. Они формируются при пересечении двух сторон параллелепипеда под прямым углом, то есть при соединении грани параллелепипеда и ее смежной грани и образуют углы в 90 градусов.
Значимость правильных прямоугольных углов связана с возможностью применения параллелепипеда в различных отраслях науки, техники и строительства. Благодаря своей форме и структуре, прямоугольный параллелепипед применяется в архитектуре, для создания прочных и устойчивых конструкций.
В строительстве используются предметы с правильными прямоугольными углами, такие как кирпич, блоки и плиты, для возведения фундаментов, стен и других элементов зданий. Также прямоугольные параллелепипеды находят применение в мебельном производстве, где служат основой для создания столов, шкафов и других предметов интерьера.
Три пары противоположных грани
Такие пары противоположных граней являются особенностью формы и свойства прямоугольного параллелепипеда. Они позволяют ему иметь определенные характеристики, такие как равенство площадей противоположных граней и равенство углов между плоскостями, проходящими через противоположные ребра.
Три пары противоположных граней также определяют форму и размеры параллелепипеда. Например, если все грани параллелепипеда прямоугольные, то он называется прямоугольным. В противном случае, если хотя бы одна грань не является прямоугольной, параллелепипед называется неправильным.
Равные стороны и ребра
Прямоугольный параллелепипед имеет не только прямоугольное основание, но и равные стороны и ребра. Вот основные черты этой формы:
| Стороны | Ребра |
|---|---|
| Две пары противоположных сторон имеют одинаковые длины и параллельны друг другу. | Все ребра параллелепипеда также равны между собой и образуют прямые углы с плоскостями основания. |
| Длина одной пары сторон может быть разной, но внутри каждой пары стороны равны. | Все шесть ребер параллелепипеда имеют одинаковую длину. |
Равные стороны и ребра прямоугольного параллелепипеда позволяют ему обладать определенными свойствами, такими как равномерность и симметричность. Эти черты делают его удобным для различных задач и областей применения.
Свойства прямоугольного параллелепипеда
Основные свойства прямоугольного параллелепипеда:
- Форма. У прямоугольного параллелепипеда все грани являются прямоугольниками. Это делает эту фигуру очень удобной для многих практических задач.
- Все ребра равны попарно. В прямоугольном параллелепипеде все ребра, соединяющие противоположные вершины, равны друг другу.
- Углы. Все углы прямоугольного параллелепипеда равны 90 градусам.
- Диагонали. Диагонали, соединяющие противоположные вершины, равны друг другу и делят фигуру на равные треугольники.
- Объем и площади. Объем прямоугольного параллелепипеда равен произведению длины, ширины и высоты, а площадь его поверхности вычисляется по формуле: S = 2lw + 2lh + 2wh, где l, w и h — длина, ширина и высота соответственно.
Прямоугольный параллелепипед находит широкое применение в различных областях, таких как строительство, математика, геометрия и инженерия.
Объем и площадь поверхности
Объем прямоугольног
Симметрия и преобразования
Симметрия — это особенность фигуры, когда она может быть разделена на две части, которые являются зеркальным отражением друг друга. В случае прямоугольного параллелепипеда, он обладает несколькими видами симметрии. Во-первых, у него есть граневая симметрия — каждая грань параллелепипеда может быть разделена на две одинаковые части.
Кроме того, у прямоугольного параллелепипеда есть центральная симметрия — если мы проведем ось симметрии через центр параллелепипеда, то любая точка на одной стороне относительно оси будет иметь точно соответствующую ей точку на противоположной стороне от оси.
Кроме симметрии, прямоугольный параллелепипед обладает свойством преобразований. Такие преобразования, как поворот, смещение и масштабирование, могут быть применены к параллелепипеду, не меняя его форму и свойства. Эти преобразования могут быть использованы, чтобы изменять положение и размеры параллелепипеда, сохраняя его особенную форму — прямоугольную.
Таким образом, симметрия и преобразования играют важную роль в характеристиках прямоугольного параллелепипеда, определяя его форму и свойства. Эти концепции помогают нам лучше понять и визуализировать эту особенную фигуру в математике и геометрии.
Диагонали и углы прямоугольного параллелепипеда
Одной из важных характеристик прямоугольного параллелепипеда являются его диагонали. Диагонали параллелепипеда — это прямые линии, соединяющие противоположные вершины этого тела. У прямоугольного параллелепипеда имеется три основные диагонали: две диагонали основания и диагональ внутри параллелепипеда.
Диагонали основания параллелепипеда имеют одинаковую длину и являются главными диагоналями. Они определяют его максимальную длину и высоту. Длина главной диагонали можно вычислить по теореме Пифагора.
Диагональ внутри параллелепипеда соединяет противоположные вершины граней и называется пространственной диагональю. Ее длина также вычисляется по теореме Пифагора.
Углы прямоугольного параллелепипеда имеют такие же меры, как и углы прямоугольника. Они составляют 90 градусов и обозначаются символом «∠». Всего в прямоугольном параллелепипеде шестнадцать прямых углов, по четыре угла в каждом из восьми вершин.
Диагонали и углы являются важными характеристиками прямоугольного параллелепипеда, они используются при решении различных геометрических задач и определении его формы и свойств.
Вопрос-ответ:
Что такое параллелепипед?
Параллелепипед — это геометрическое тело, у которого все грани являются прямоугольниками и параллельны друг другу.
Какие свойства имеет прямоугольный параллелепипед?
Прямоугольный параллелепипед обладает рядом особенных свойств: все его углы прямые, диагонали граней равны, объем равен произведению длин трех ребер, площадь поверхности вычисляется суммой площадей граней.
Как определить, что параллелепипед является прямоугольным?
Параллелепипед может быть определен как прямоугольный, если все его углы прямые. Это можно проверить, измерив углы между гранями параллелепипеда.
Какие формы граней могут иметь прямоугольный параллелепипед?
Грани прямоугольного параллелепипеда имеют форму прямоугольника. Всего у прямоугольного параллелепипеда 6 граней.
Как вычислить объем прямоугольного параллелепипеда?
Объем прямоугольного параллелепипеда можно вычислить, умножив длину, ширину и высоту параллелепипеда.