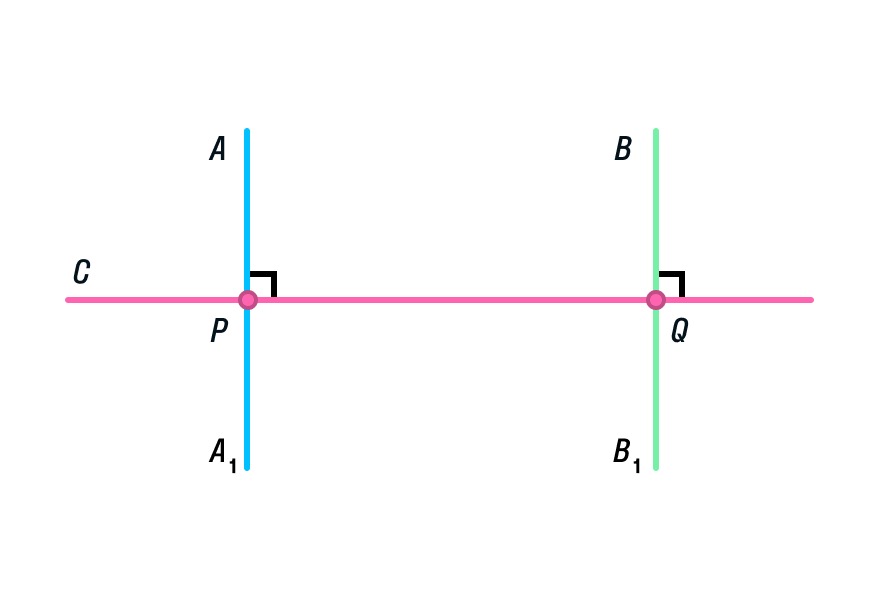
Плоскость — это геометрическая конструкция, которая состоит из бесконечного числа точек. Прямая — это одномерный геометрический объект, состоящий из бесконечного числа точек, у которых есть общее направление. Интересно, что на плоскости можно найти такие две прямые, которые не пересекаются.
Эти две прямые могут располагаться параллельно друг другу. Они не пересекаются ни в одной точке. Такие прямые называются параллельными. Каждая из них продолжается до бесконечности и никогда не сойдется.
Понятие параллельности является важным элементом геометрии и имеет множество применений. Например, в архитектуре, параллельные линии используются для создания эффекта перспективы и глубины. В математике параллельные прямые играют важную роль в теореме Пифагора и теореме Талеса.
На плоскости: две параллельные прямые
Если провести параллельные прямые на чертеже, то они будут расположены рядом друг с другом и будут иметь одинаковую ориентацию. В геометрии можно провести бесконечное количество параллельных прямых к данной прямой.
Понятие параллельных прямых имеет большое значение в геометрии и использования их на практике. Например, в архитектуре параллельные прямые используются для создания перпендикулярных линий и равномерной геометрической формы зданий. Также, в математике и физике параллельные прямые используются для моделирования пространственных взаимодействий и определения углов наклона.
В геометрии параллельные прямые могут быть определены с помощью альтернативных углов, составляющихся при пересечении прямых третьей прямой. Если альтернативные углы равны, то прямые являются параллельными.
Итак, параллельные прямые — это две прямые, которые не пересекаются и находятся на одной плоскости. Они играют важную роль в геометрии и имеют множество практических применений.
Понятие и свойства
Прямые, которые не пересекаются, могут быть параллельными. Параллельные прямые имеют одно и то же направление, они никогда не пересекаются, даже при продолжении за пределы видимой плоскости. Параллельные прямые расстояние между ними постоянно и всегда одинаково.
Если две прямые не пересекаются и не параллельны, то их направления различны. Такие прямые имеют общую точку пересечения, которая является началом координат плоскости. Они могут быть наклонными, то есть иметь разные углы наклона относительно осей координат.
| Тип прямых | Описание | Пример |
|---|---|---|
| Пересекающиеся прямые | Две прямые, которые пересекаются в одной точке. |  |
| Параллельные прямые | Две прямые, которые никогда не пересекаются. |  |
| Наклонные прямые | Две прямые, которые не параллельны, но не пересекаются. |  |
Изучение свойств этих прямых помогает понять и использовать их в различных математических и геометрических задачах.
Определение параллельных прямых
va = k * vb,
где k — коэффициент пропорциональности. Если две прямые параллельны, то их углы наклона равны. Также можно использовать теорему о параллельных и пересекающихся прямых: если две прямые параллельны третьей прямой, то они параллельны друг другу.
Структура и свойства параллельных прямых
Одно из основных свойств параллельных прямых заключается в том, что они имеют одинаковый угол наклона, то есть угол между прямыми и осью абсцисс (осью Х) или осью ординат (осью Y) будет одинаковым.
Также важным свойством параллельных прямых является то, что расстояние между ними постоянно. Это расстояние называется параллельным перпендикуляром и принимает одно и то же значение в любых точках параллельных прямых.
Из-за своей структуры и взаимного расположения, параллельные прямые имеют ряд важных геометрических приложений. Например, они используются при построении параллелограммов, треугольников и других фигур. Также параллельные прямые формируют базис для определения углов и длин отрезков на плоскости.
Параллельные прямые играют важную роль в различных областях, таких как геометрия, физика, инженерия и архитектура. Знание и понимание их структуры и свойств позволяет решать разнообразные задачи, связанные с расчетами, измерениями и конструкциями на плоскости.
Примеры параллельных прямых в геометрии
Примером параллельных прямых являются параллельные линии на дороге. Они идут рядом друг с другом и никогда не пересекаются.
Другим примером являются рельсы железнодорожных путей. Рельсы, идущие параллельно друг другу, образуют пару параллельных прямых.
Еще одним примером параллельных прямых может служить пара вертикальных стволов деревьев, которые растут на одном расстоянии друг от друга и никогда не сталкиваются.
В геометрии параллельные прямые играют важную роль, так как они имеют множество свойств и используются в различных математических задачах и конструкциях.
На плоскости: две скрещивающиеся прямые
Скрещивающиеся прямые – это две прямые, которые пересекаются и образуют точку пересечения. Точка пересечения – это общая точка на обеих прямых, в которой они пересекаются. Определение скрещивающихся прямых может быть представлено с помощью таблицы.
| Положение прямых | Описание |
|---|---|
| Скрещивающиеся прямые | Две прямые пересекаются и имеют одну точку пересечения. |
| Параллельные прямые | Две прямые не пересекаются и всегда имеют одно и то же направление. |
| Совпадающие прямые | Две прямые лежат на одной прямой, они совпадают и имеют бесконечное количество точек пересечения. |
Скрещивающиеся прямые – это особый случай, который иногда называют пересекающимися прямыми. Они могут быть представлены в виде графика на плоскости, где точка пересечения двух прямых обозначается как точка с координатами (x, y).
Знание о скрещивающихся прямых может быть полезным в решении различных задач и заданий, связанных с геометрией. Определение положения прямых на плоскости является одним из ключевых аспектов изучения геометрии, и умение распознавать и анализировать скрещивающиеся прямые поможет вам лучше понять пространственные отношения и решать геометрические задачи.
Понятие и свойства
Две прямые, не пересекающиеся на плоскости, обладают рядом особых свойств.
1. Параллельность: Если две прямые не пересекаются, то они называются параллельными. Это означает, что они находятся на одной плоскости, но никогда не пересекаются.
2. Расстояние между прямыми: Расстояние между двумя параллельными прямыми постоянно и равно. Оно измеряется перпендикулярно к прямым.
3. Угол между прямыми: Угол между двумя параллельными прямыми равен 180 градусам.
4. Плоскости, параллельные прямым: Две параллельные прямые определяют плоскость, которая также параллельна вашим прямым. Это означает, что любая другая прямая на этой плоскости будет параллельна исходным прямым.
5. Прямая, пересекающая прямые: Если третья прямая пересекает две параллельные прямые, то она называется трансверсальной. Она формирует специальные углы с этими прямыми, такие как вертикальные и соответственные углы.
6. Нет решений: По определению, две параллельные прямые никогда не пересекаются и не имеют общих точек. Следовательно, система уравнений с такими прямыми не имеет решений.
Эти свойства параллельных прямых важны для геометрии и применяются в различных областях науки и технологии.
Вопрос-ответ:
Для чего нужна информация о двух прямых, которые не пересекаются на плоскости?
Информация о двух прямых, которые не пересекаются на плоскости, может быть полезна в различных областях, например, в геометрии, графике, а также в решении задач, связанных с построением линейных моделей.
Какие характеристики обладают две прямые, которые не пересекаются на плоскости?
Две прямые, которые не пересекаются на плоскости, являются параллельными. Это значит, что они расположены на одной плоскости и никогда не пересекаются, даже если мы продлеваем их до бесконечности.
Что такое параллельные прямые?
Параллельные прямые — это прямые, которые находятся на одной плоскости и никогда не пересекаются. Они имеют одинаковые углы наклона и бесконечно продолжаются в одном и том же направлении.
Как можно определить, пересекаются ли две прямые на плоскости или нет?
Для определения пересечения двух прямых на плоскости можно рассмотреть их уравнения. Если система уравнений, задающая прямые, не имеет решений, то прямые не пересекаются. Если же система имеет единственное решение, то прямые пересекаются в точке, определяемой этим решением.
Каким образом можно построить две прямые, которые не пересекаются на плоскости?
Для построения двух прямых, которые не пересекаются на плоскости, можно использовать метод геометрической конструкции с помощью чертежей и инструментов. Например, для построения параллельных прямых можно провести линию и через точку на ней провести прямую, которая не пересекает первую.
Какие две прямые на плоскости не пересекаются?
На плоскости существует бесконечное количество прямых, которые не пересекаются. Две прямые могут быть параллельными, то есть иметь одинаковый угловой коэффициент и не пересекаться никогда. Это может случиться, например, если прямые имеют уравнения y = 2x + 3 и y = 2x + 5. В таком случае, прямые идут вдоль друг друга, но никогда не пересекаются. Еще одним примером параллельных прямых являются горизонтальные и вертикальные прямые. Горизонтальные прямые имеют одинаковое значение y и не имеют общих точек, а вертикальные прямые имеют одинаковое значение x и тоже не пересекаются. Таким образом, существует множество параллельных прямых, которые на плоскости не пересекаются.
Могут ли две прямые на плоскости не иметь общих точек?
Да, две прямые на плоскости могут не иметь общих точек. В таком случае, прямые называются параллельными. Параллельные прямые имеют одинаковый угловой коэффициент, что означает, что они идут в одном и том же направлении, но никогда не пересекаются. Например, прямые с уравнениями y = 3x + 2 и y = 3x + 5 параллельны и не имеют общих точек. Они идут вдоль друг друга, но никогда не пересекаются. Таким образом, параллельные прямые на плоскости не имеют общих точек и не пересекаются.