Какой треугольник считается остроугольным определение и свойства

Остроугольный треугольник – это треугольник, у которого все его углы острые, то есть меньше 90 градусов. Остроугольные треугольники являются одним из видов треугольников, которые можно классифицировать по свойствам их углов и сторон.

Остроугольный треугольник является противоположностью тупоугольного треугольника, у которого один из углов больше 90 градусов. Это важное свойство остроугольного треугольника влияет на его геометрические и тригонометрические характеристики, а также на его потенциальное использование в различных математических задачах.

Для определения остроугольного треугольника необходимо измерить все его углы с помощью угломера или основных геометрических формул. Если каждый из углов треугольника меньше 90 градусов, то треугольник можно считать остроугольным. Угловая сумма остроугольного треугольника всегда будет равна 180 градусам, что является еще одним его важным свойством.

Содержание

Остроугольный треугольник: определение и свойства

Чтобы определить, является ли треугольник остроугольным, нужно вычислить все его углы. Если все углы меньше 90 градусов, то треугольник является остроугольным.

Свойства остроугольного треугольника:

В остроугольном треугольнике все стороны являются основой для острого угла. Это означает, что каждая сторона больше расстояния от вершины острого угла до точки пересечения высот, проведенных из двух острых углов.
В остроугольном треугольнике сумма длин двух сторон всегда больше длины третьей стороны.
Остроугольный треугольник может быть равнобедренным, то есть иметь две равные стороны и два равных угла.
Остроугольный треугольник может быть равносторонним, то есть иметь три равные стороны и три равных угла, каждый из которых равен 60 градусам.

Остроугольные треугольники широко применяются в геометрии и углубленных математических исследованиях. Наличие острых углов в треугольнике имеет важные геометрические свойства, которые позволяют решать разнообразные задачи и проводить анализ различных геометрических фигур.

Определение остроугольного треугольника

Остроугольным треугольником называется треугольник, у которого все углы острые, то есть меньше 90 градусов. Угол считается острым, если его мера находится в интервале от 0 до 90 градусов.

Остроугольный треугольник обладает следующими свойствами:

Все его углы острые;
Сумма мер всех углов треугольника равна 180 градусов;
Наибольшая сторона остроугольного треугольника лежит против наибольшего угла, а наименьшая сторона — против наименьшего угла.

Остроугольные треугольники имеют множество применений в геометрии и на практике. Они обладают определенными свойствами и характеристиками, которые определяют их форму и структуру.

Остроугольный треугольник: основные характеристики

Основные характеристики остроугольного треугольника:

Углы острого треугольника меньше 90 градусов;
Сумма всех углов треугольника всегда равна 180 градусов;
Остроугольный треугольник обладает меньшей степенью площади по сравнению с прямоугольным или тупоугольным треугольником;
В остроугольном треугольнике нет прямого угла, следовательно, у него нет высоты, опущенной из острого угла;
Остроугольный треугольник может быть равносторонним, равнобедренным или разносторонним, в зависимости от длин сторон.

Из-за своих особых свойств, остроугольный треугольник имеет широкий спектр применений в геометрии, физике и других науках. Например, он является основой для расчета тригонометрических функций, а также используется для определения точек пересечения прямых и плоскостей или для измерения углов в пространстве.

Математическое определение остроугольного треугольника

Остроугольный треугольник отличается от тупоугольного треугольника, у которого один из углов больше 90 градусов, и от прямоугольного треугольника, у которого один из углов равен 90 градусам.

В остроугольном треугольнике все стороны положительны и меньше суммы длин двух других сторон. Это свойство называется неравенством треугольника. Если сторона треугольника больше или равна сумме длин двух других сторон, то такой треугольник не может существовать.

Остроугольный треугольник	Тупоугольный треугольник	Прямоугольный треугольник

Свойства остроугольного треугольника

Свойства остроугольного треугольника:

1. Все стороны остроугольного треугольника положительны и меньше суммы двух других его сторон.

Это свойство можно сформулировать следующим образом: длина каждой стороны остроугольного треугольника меньше суммы длин двух других его сторон. Например, для сторон треугольника со сторонами a, b и c это свойство можно записать как:

a < b + c

b < a + c

c < a + b

2. Сумма всех углов остроугольного треугольника равна 180 градусов.

Так как все углы острые, то их сумма обязательно будет равна 180 градусов. Например, если у вас есть треугольник с углами 𝑎, 𝑏 и 𝑐, где 𝑎 < 90°, 𝑏 < 90° и 𝑐 < 90°, то:

𝑎 + 𝑏 + 𝑐 = 180°

3. Остроугольный треугольник является выпуклым.

Выпуклый треугольник – это треугольник, у которого все его углы острые. Это свойство подразумевает, что все его углы направлены внутрь треугольника, а не внешне.

Эти свойства остроугольного треугольника являются необходимыми и существенными для данного типа треугольника. Они помогают в понимании его формы и свойств, а также в решении различных задач, связанных с остроугольными треугольниками.

Остроугольный треугольник и углы

У остроугольного треугольника есть несколько свойств:

Сумма всех трех углов треугольника равна 180 градусов.
Каждый из углов треугольника должен быть меньше 90 градусов, чтобы треугольник был остроугольным.
Остроугольный треугольник может быть равносторонним, равнобедренным или разносторонним.
В равностороннем треугольнике все углы равны 60 градусов и каждая сторона имеет одинаковую длину.
В равнобедренном треугольнике два угла и две стороны равны.
В разностороннем треугольнике все углы и все стороны имеют разные значения.

Остроугольные треугольники играют важную роль в геометрии и могут использоваться для решения различных математических задач.

Остроугольный треугольник и стороны

Строение остроугольного треугольника влияет на длины его сторон. В случае, когда все углы треугольника острые, длины его сторон тоже имеют определенные свойства:

В остроугольном треугольнике все стороны положительны, так как их длины всегда больше нуля.
Сумма длин любых двух сторон остроугольного треугольника всегда больше длины третьей стороны.
Наименьшей стороной остроугольного треугольника всегда является сторона, противолежащая наименьшему углу.
Наибольшей стороной остроугольного треугольника всегда является сторона, противолежащая наибольшему углу.

Остроугольный треугольник обладает своими особенностями и изучается в геометрии для решения различных задач и вычислений.

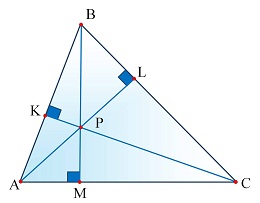
Остроугольный треугольник и высоты

Острые углы треугольника имеют важное значение при построении высот. Высотой треугольника называется отрезок, проведенный из вершины треугольника до противоположной стороны и перпендикулярный данной стороне.

Для остроугольных треугольников выполняется следующее свойство: все высоты пересекаются в одной точке, называемой ортоцентром.

Остроугольный треугольник может иметь три высоты, каждая из которых проходит через одну из вершин и перпендикулярна соответствующей стороне. Высоты могут служить основой для нахождения других величин, таких как площадь треугольника и его биссектрисы.

Вопрос-ответ:

Что такое остроугольный треугольник?

Остроугольный треугольник — это треугольник, у которого все углы острые, то есть меньше 90 градусов.

Как определить, является ли треугольник остроугольным?

Чтобы определить, является ли треугольник остроугольным, нужно проверить все его углы: если все они меньше 90 градусов, то треугольник является остроугольным.