Котангенс — одна из основных тригонометрических функций, которая используется для нахождения отношения сторон прямоугольного треугольника. Котангенс является обратной функцией к тангенсу и определяется как отношение противолежащего катета к прилежащему катету. Она позволяет вычислить угол по отношению сторон треугольника и представляет собой дробь.
Для нахождения котангенса острого угла прямоугольного треугольника необходимо разделить длину противолежащего катета на длину прилежащего катета. Котангенсом обозначается как ctg или ctn. Эта величина позволяет определить, сколько раз противолежащий катет больше прилежащего.
Котангенс полезен при решении геометрических задач и в вычислительной математике. Он может быть использован для нахождения прямоугольного треугольника с заданным углом и сторонами, а также для определения противолежащего катета или прилежащего катета, если известны другие параметры.
Котангенс острого угла
cot(A) = adj/hyp
Где:
- cot(A) — котангенс острого угла
- adj — прилежащий катет, расположенный рядом с углом A
- hyp — гипотенуза треугольника
Значение котангенса острого угла позволяет определить соотношение между сторонами треугольника. Также этот параметр может быть использован для решения задач, связанных с треугольниками, синусами и косинусами углов.
Важно отметить, что котангенс острого угла может быть вычислен не только для прямоугольных треугольников, но и для любого острого угла в треугольнике.
Определение и обозначение
Котангенсом острого угла прямоугольного треугольника называется отношение длины его катета, лежащего напротив данного угла, к длине прилежащего катета. Котангенс обозначается как ctg или ctn.
Связь с другими тригонометрическими функциями
Котангенсом острого угла прямоугольного треугольника называется отношение стороны прилегающего катета к противолежащему катету. Он обозначается как ctg и выражается формулой:
ctg(θ) = b/a
где θ — острый угол треугольника, b — прилегающий катет, a — противолежащий катет.
Связь котангенса с другими тригонометрическими функциями определяется следующими соотношениями:
1. Синус и котангенс:
Синус острого угла равен отношению противолежащего катета к гипотенузе, а котангенс — отношению прилегающего катета к противолежащему:
sin(θ) = b/c и ctg(θ) = b/a
Таким образом, можно получить выражение для котангенса через синус:
ctg(θ) = (1/sin(θ)) = c/b
2. Косинус и котангенс:
Косинус острого угла равен отношению прилегающего катета к гипотенузе, а котангенс — отношению прилегающего катета к противолежащему:
cos(θ) = a/c и ctg(θ) = b/a
Следовательно, можно выразить котангенс через косинус:
ctg(θ) = (1/cos(θ)) = c/a
Таким образом, котангенс является обратной функцией к тангенсу и имеет связь с синусом и косинусом острого угла прямоугольного треугольника.
Значения котангенса острого угла
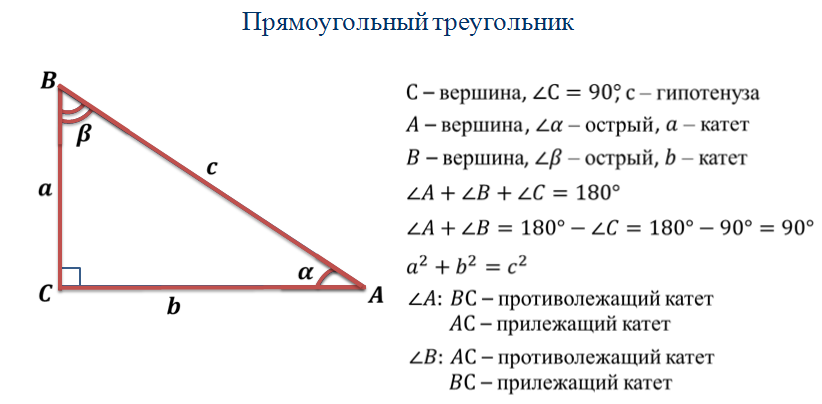
Котангенсом острого угла прямоугольного треугольника называется отношение длины катета, примыкающего к данному углу, к длине другого катета, примыкающего к прямому углу.
Значения котангенса острого угла можно посчитать для углов от 0 до 90 градусов. В таблице ниже представлены значения котангенса острого угла для некоторых углов:
| Острый угол (градусы) | Котангенс |
|---|---|
| 0 | ∞ |
| 30 | √3 |
| 45 | 1 |
| 60 | √3/3 |
| 90 | 0 |
Значение котангенса для угла 0 градусов равно бесконечности, так как длина противолежащего катета равна 0. Значение котангенса для угла 90 градусов равно 0, так как длина примыкающего катета равна 0.
Значение котангенса для угла 45 градусов равно 1, так как в прямоугольном треугольнике с углом 45 градусов длина обоих катетов равна x, а гипотенуза равна √2x. Подставляя значения в определение котангенса, получим: котангенс(45°) = √2x/x = 1.
Значения котангенса для углов 30 и 60 градусов можно также вывести с помощью геометрических соображений или использовать дополнительные формулы из тригонометрии.
Таблица значений котангенса
Котангенсом острого угла прямоугольного треугольника называется отношение, обратное тангенсу этого угла. Котангенс угла равен отношению длины прилежащего катета к длине противолежащего катета.
Для удобства использования котангенса и построения графиков и функций, приведена таблица значений котангенса основных углов от 0° до 90°:
| Угол (градусы) | Котангенс |
|---|---|
| 0 | ∞ |
| 15 | 1.73 |
| 30 | 1.00 |
| 45 | 1.00 |
| 60 | 1.73 |
| 75 | ∞ |
| 90 | 0 |
Значения котангенса могут быть использованы в различных задачах и вычислениях, где требуется нахождение отношения длин сторон прямоугольного треугольника.
Свойства котангенса
Котангенсом острого угла прямоугольного треугольника называется отношение, равное отношению катета, примыкающего к данному углу, к катету, противоположному данному углу.
Свойства котангенса:
- 1. Котангенс острого угла всегда положителен.
- 2. Котангенс острого угла убывает с ростом значения угла от 0 до 90 градусов.
- 3. Котангенс угла в прямоугольном треугольнике равен отношению смежного катета к противоположному катету, то есть cotA = adjacent/opposite.
- 4. Котангенс острого угла равен обратному тангенсу данного угла: cotA = 1/tanA .
Котангенс является одной из тригонометрических функций, которая широко применяется в математике и физике для решения задач, связанных с прямоугольными треугольниками и тригонометрическими соотношениями.
Применение котангенса
1. Решение задач треугольников
Котангенс острого угла прямоугольного треугольника можно использовать для нахождения его сторон и углов. Если известны значения двух сторон или одной стороны и одного угла треугольника, то можно использовать котангенс, чтобы вычислить остальные неизвестные величины.
2. Инженерные расчеты
Котангенс применяется в различных инженерных расчетах, таких как проектирование строительных конструкций, дорожное строительство, гидротехнические сооружения и другие. Например, котангенс может использоваться для определения углов наклона скатов крыш, что является важной задачей при проектировании кровли.
3. Физические расчеты
Котангенс применяется в физических расчетах, особенно в механике и электротехнике. Например, котангенс может использоваться для определения векторного направления силы или момента, а также для нахождения угла между ними.
4. Компьютерная графика
Котангенс используется в компьютерной графике для решения задач, связанных с преобразованиями и изменением формы объектов. Например, при создании трехмерной модели объекта котангенс может быть использован для определения угла наклона поверхности и ее дальнейшей деформации.
Таким образом, котангенс является важной математической функцией, которая находит применение во многих областях науки и техники.
Задачи с использованием котангенса
Котангенс острого угла прямоугольного треугольника вычисляется как отношение катета, примыкающего к данному углу, к катету, лежащему напротив данного угла. Котангенс широко применяется в решении различных математических задач.
Задача 1: Нахождение неизвестного катета
Пусть у нас есть прямоугольный треугольник со сторонами a, b и гипотенузой c. Известно, что один из острых углов треугольника равен α. Требуется найти значение неизвестного катета b.
Для решения этой задачи можно использовать котангенс. Зная значение угла α, можно выразить котангенс этого угла как отношение известного катета a к неизвестному катету b:
cot(α) = a/b
Перегруппировав и применив котангенс, получим:
b = a/cot(α)
Используя данную формулу, можно легко найти значение неизвестного катета b.
Задача 2: Нахождение высоты треугольника
Пусть у нас есть прямоугольный треугольник со сторонами a и b и гипотенузой c. Известно, что один из острых углов треугольника равен α. Требуется найти значение высоты треугольника h.
Для решения этой задачи можно также использовать котангенс. Зная значение угла α, можно выразить котангенс этого угла как отношение известного катета b к высоте треугольника h:
cot(α) = b/h
Перегруппировав и применив котангенс, получим:
h = b/cot(α)
Таким образом, зная значение угла α и известную сторону b, можно вычислить значение высоты треугольника h.
| Условие задачи | Решение |
|---|---|
| Задача 1: Нахождение неизвестного катета | Известны сторона a, угол α и гипотенуза c. Найти b. |
| Задача 2: Нахождение высоты треугольника | Известны сторона b, угол α и гипотенуза c. Найти h. |
Полезные советы по вычислению котангенса
Котангенсом острого угла прямоугольного треугольника называется отношение длины катета, заключенного между гипотенузой и прямым углом, к длине гипотенузы.
Для вычисления котангенса острого угла треугольника можно использовать формулу:
cot(A) = adj / opp
где:
- cot(A) — котангенс острого угла A;
- adj — длина прилегающего катета;
- opp — длина противолежащего катета.
Чтобы правильно вычислить котангенс, важно знать значения длин прилегающего катета и противолежащего катета. Также нужно убедиться, что угол, для которого требуется вычислить котангенс, является острым.
Помни, что котангенс зависит только от соотношения длин катетов и гипотенузы и не зависит от размеров самого треугольника.
Используя эти полезные советы, ты сможешь легко и точно вычислить котангенс острого угла прямоугольного треугольника.
Вопрос-ответ:
Зачем нужен котангенс острого угла прямоугольного треугольника?
Котангенс острого угла прямоугольного треугольника используется для вычисления высоты, основания или других сторон треугольника, если известны его углы.
Как вычислить котангенс острого угла прямоугольного треугольника?
Чтобы вычислить котангенс острого угла прямоугольного треугольника, необходимо разделить длину прилежащего катета к данному углу на длину противолежащего катета.
Какой символ используется для обозначения котангенса?
В математике котангенс обозначается как ctg.
Как связаны котангенс и тангенс острого угла прямоугольного треугольника?
Котангенс острого угла прямоугольного треугольника является обратным значением тангенса этого же угла. То есть, если tg(alpha) = a/b, то ctg(alpha) = b/a.
Можно ли вычислить котангенс прямого угла?
Нет, нельзя. Котангенс прямого угла равен бесконечности, так как в прямоугольном треугольнике длина противолежащего катета равна нулю.
Зачем нужен котангенс острого угла прямоугольного треугольника?
Котангенс острого угла прямоугольного треугольника используется для вычисления этого угла по известным значениям катетов или гипотенузы треугольника. Также он может применяться в решении задач с использованием тригонометрии.
Как вычислить котангенс острого угла прямоугольного треугольника?
Для вычисления котангенса острого угла прямоугольного треугольника необходимо знать значения катетов или гипотенузы треугольника и использовать следующую формулу: катет противолежащий острому углу / катет прилежащий к острому углу. Например, если известны значения катета a и гипотенузы c, котангенс угла A будет равен c / a.