Отрезок — это прямая линия, которая соединяет две точки на окружности. Когда мы говорим о соединении точек на окружности, мы часто используем другое терминологическое понятие — хорда.
Хорда — это прямая линия, которая соединяет две точки на окружности. Она является одним из основных элементов геометрических вычислений и широко используется в различных науках и инженерных областях.
Хорда имеет свои свойства и атрибуты, которые позволяют нам анализировать геометрические и физические характеристики окружностей. Одно из главных свойств хорды — ее длина. Для изучения хорды необходимо знать две важные точки, которые она соединяет.
Что такое отрезок на окружности?
Отрезок на окружности может быть задан двумя точками – начальной и конечной. Длина отрезка на окружности равна длине дуги, которую он перекрывает на окружности.
Отрезок на окружности играет важную роль в геометрии. Он используется, например, для определения углов, касательных и секущих на окружности. Кроме того, отрезок на окружности часто используется в задачах, связанных с измерением и расчетами на окружностях.
Отрезок на окружности: определение и свойства
Основные свойства отрезков на окружности:
- Длина отрезка на окружности выражается в радианах или градусах и зависит от угла, образованного этим отрезком.
- Длина отрезка на окружности равна произведению длины окружности на соответствующую часть угла в радианах.
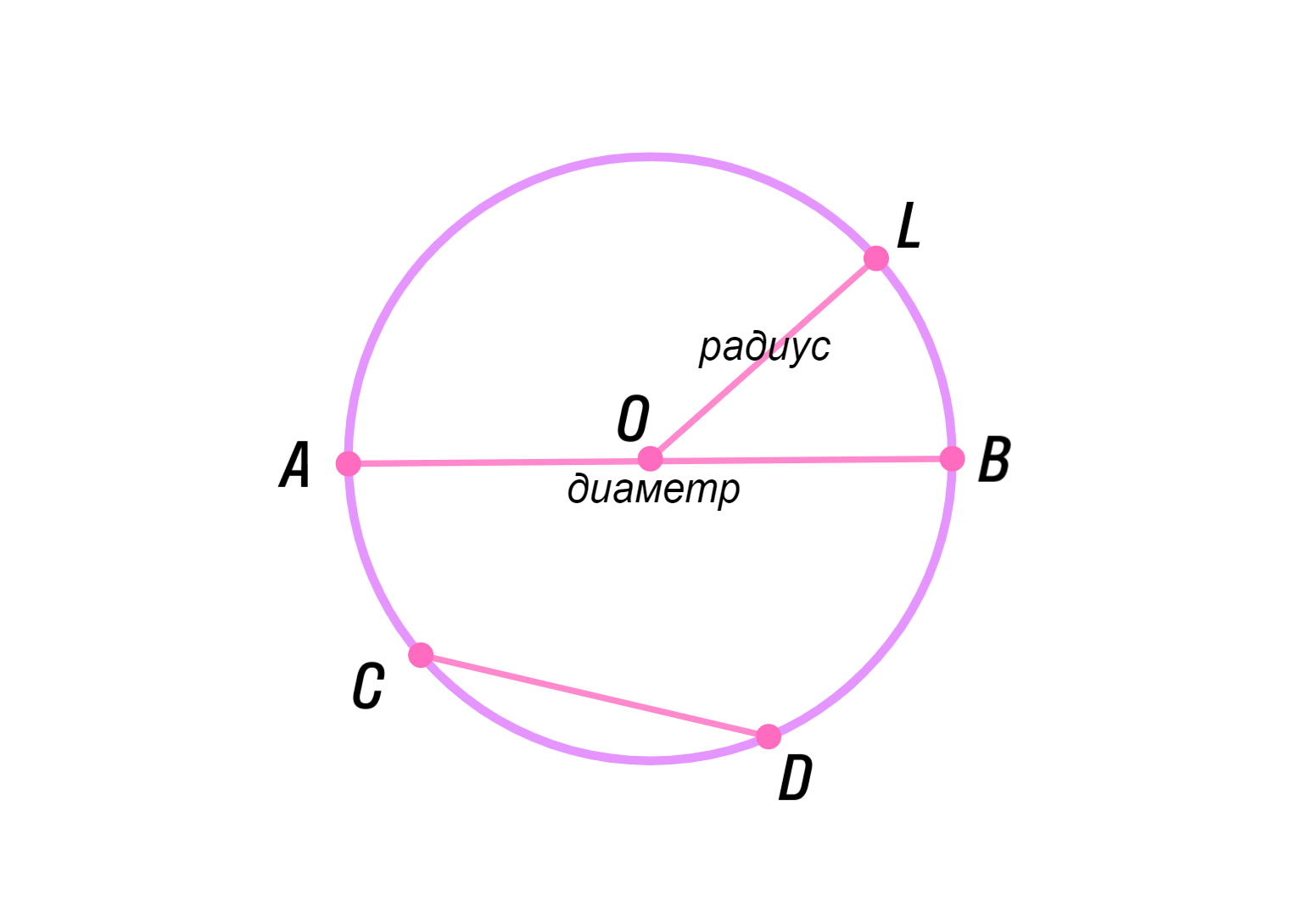
- Отрезки на окружности имеют различные названия, в зависимости от их положения и свойств. Например, если отрезок соединяет две точки на окружности и проходит через центр окружности, он называется диаметром. Если отрезок не проходит через центр окружности, он называется хордой.
- Отрезки на окружности могут быть различной длины, в зависимости от положения точек на окружности и их удаленности друг от друга.
Отрезки на окружности играют важную роль в геометрии и находят применение в различных областях, таких как физика, инженерия, астрономия и многие другие.
Определение отрезка на окружности
Длина хорды может быть вычислена с использованием геометрических формул. Для этого можно воспользоваться теоремой Пифагора: длина хорды равна квадратному корню из разности квадратов радиуса окружности и высоты, опущенной на хорду.
Хорда может быть диаметром окружности, если она проходит через ее центр, в таком случае она делит окружность на две половины и имеет максимальную длину.
Отрезок на окружности также может быть называться дугой. Дуга — это часть окружности, ограниченная двумя точками и сектором, образованным хордой и дугой.
Определение отрезка на окружности имеет важное значение в геометрии и может быть использовано для решения различных задач и задач.
Свойства отрезка на окружности
Свойства хорды на окружности:
- Хорда делит окружность на две дуги.
- Хорда, проходящая через центр окружности, называется диаметром. Диаметр является самой длинной хордой на окружности и делит ее на две половины, которые являются равными дугами.
- Если две хорды равны, то их дуги также равны.
- Теорема о перпендикулярности: если хорда перпендикулярна радиусу окружности, то она делит радиус на две равные части.
- Если точка лежит на хорде, то отрезки, соединяющие эту точку с концами хорды, равны между собой.
- Точка пересечения хорд, прямых или радиусов лежит на окружности.
Примеры использования отрезков на окружности
Отрезки на окружности используются в различных областях. Например, в геометрии отрезок, соединяющий две точки на окружности, называется хордой. Хорды активно используются при изучении секущих углов, нахождении площадей сегментов окружности и трапеций.
Также хорды на окружности используются в музыке. Круговые проходы диатонических ладов на инструментах, таких как гитара или фортепиано, часто представлены в виде отрезков на окружности. Исполнители используют эти хорды для создания разнообразных аккордов и мелодий.
Отрезки на окружности также важны в навигации и картографии. Они помогают определить направление и расстояние между двумя точками на земной поверхности. Такие отрезки используются при построении маршрутов или при определении географических координат точек.
Кроме того, отрезки на окружности используются в архитектуре и дизайне. Например, при создании круглых арок или колонн часто используются отрезки, соединяющие точки на окружности. Это позволяет создать эстетически приятные и гармоничные формы.
Использование отрезков на окружности в различных областях позволяет нам более точно определить расстояние, направление или создать красивые и функциональные объекты. Они являются важным элементом при решении различных задач и задействованы в различных областях нашей жизни.
Название отрезка на окружности
Отрезок, соединяющий две точки на окружности, называется хордой.
Хорда является прямой линией, которая соединяет две точки на окружности и лежит внутри самой окружности. Хорда также может быть равна диаметру, если проходит через центр окружности.
Хорды играют важную роль в геометрии окружностей и имеют много свойств и характеристик. Например, если две хорды пересекаются внутри окружности, то произведения отрезков каждой хорды равны.
Другим важным свойством хорды является ее длина. Длина хорды может быть вычислена с использованием теоремы о перпендикулярах, если известны длины радиуса окружности и высота, опущенная из центра окружности на хорду.
Таким образом, хорда является основным понятием в геометрии окружностей и играет важную роль при решении различных задач и построения геометрических конструкций на окружности.
Расчет длины отрезка на окружности
Длина отрезка, соединяющего две точки на окружности, называется дуговой длиной или длиной дуги.
Для расчета длины дуги необходимо знать:
- Радиус окружности (R)
- Угол между двумя точками на окружности (θ)
Формула для расчета длины дуги:
L = R × θ
где L — длина дуги, R — радиус окружности, θ — угол в радианах между двумя точками на окружности.
| Угол в градусах | Угол в радианах (θ) | Длина дуги (L) |
|---|---|---|
| 90° | π/2 | πR/2 |
| 180° | π | πR |
| 360° | 2π | 2πR |
Таким образом, длина дуги на окружности зависит от радиуса и угла между точками на ней.
Вопрос-ответ:
Как называется отрезок, соединяющий две точки на окружности?
Отрезок, соединяющий две точки на окружности, называется хордой.
Можно ли увеличить длину хорды на окружности?
Да, длину хорды на окружности можно увеличить, если перемещать точки, которые она соединяет.
Что произойдет с хордой, если точки, которые она соединяет, сместить в одну сторону?
Если точки, которые соединяются хордой на окружности, сместить в одну сторону, то хорда увеличится в длине.
Может ли хорда быть диаметром окружности?
Да, хорда может быть диаметром окружности, если она проходит через центр окружности.
Существует ли ограничение на длину хорды на окружности?
Нет, длина хорды на окружности может быть любой, включая нулевую длину (когда хорда состоит из одной точки) и длину, равную длине окружности (когда хорда проходит по всей окружности).