
Понятие перпендикулярности в геометрии является одним из фундаментальных. Оно связано с взаимным расположением плоскостей и отношениями между ними. Две плоскости пересекаются, когда у них есть общая точка, но как определить, являются ли они перпендикулярными?
Перпендикулярность двух плоскостей означает, что угол между ними равен 90 градусам. Другими словами, прямая, перпендикулярная одной плоскости, будет пересекать другую плоскость под прямым углом. Это может быть представлено как вертикальное падение света на горизонтальный план, где лучи света падают перпендикулярно к плоскости земли.
Перпендикулярные плоскости часто встречаются в различных областях математики и физики. Например, они применяются при построении трехмерных моделей, расчете сил и направлений в пространстве, а также в компьютерной графике и архитектуре. Изучение перпендикулярности позволяет более точно определить положение объектов и решить различные задачи, связанные с их взаимодействием.
Что такое перпендикулярные плоскости?
Перпендикулярность плоскостей является важным концептом в геометрии и находит применение в различных областях, таких как архитектура, инженерия и физика.
Характеристики перпендикулярных плоскостей
Перпендикулярные плоскости обладают следующими характеристиками:
- Пересечение перпендикулярных плоскостей является прямой линией, лежащей в обеих плоскостях.
- Угол между перпендикулярными плоскостями равен 90 градусам.
- Линии, лежащие в перпендикулярных плоскостях и пересекающиеся, будут перпендикулярны друг другу.
Перпендикулярность плоскостей образуется, когда два вектора, ортогональные обоим плоскостям, пересекаются между собой.
Пример использования перпендикулярных плоскостей:
В архитектуре перпендикулярные плоскости используются для создания прямых углов между стенами и полами, что способствует сохранению ровных и гармоничных линий в строении.
В физике перпендикулярные плоскости используются для описания взаимного расположения объектов, например, векторов сил или электрических полей.
В инженерии перпендикулярные плоскости применяются для создания трехмерных моделей объектов и обозначения взаимного расположения их элементов.
Перпендикулярность плоскостей и их свойства
Две пересекающиеся плоскости называются перпендикулярными, если угол между ними составляет 90 градусов или, другими словами, если их нормальные векторы взаимно перпендикулярны. Такая перпендикулярность плоскостей имеет ряд важных свойств и приложений в различных областях математики и физики.
Свойства перпендикулярных плоскостей:
| Свойство | Описание |
|---|---|
| Пересечение прямой и плоскости | Если прямая пересекает первую плоскость перпендикулярно, то она пересекает и вторую плоскость перпендикулярно. |
| Угол между плоскостями | Угол между перпендикулярными плоскостями равен углу между их нормальными векторами. |
| Сложение и вычитание плоскостей | Сумма двух перпендикулярных плоскостей также является плоскостью, перпендикулярной обоим исходным плоскостям. |
| Отражение плоскости | Плоскость, отраженная от перпендикулярной плоскости, остается перпендикулярной к исходной плоскости. |
Перпендикулярность плоскостей широко применяется в геометрии, инженерии, физике и других дисциплинах. Она помогает решать задачи по построению, определению углов и направлений, а также в анализе пространственных отношений и взаимодействий объектов.
Пересечение перпендикулярных плоскостей
Пересечение перпендикулярных плоскостей образует линию, которая называется прямой пересечения. Эта линия является прямой, так как она лежит в двух плоскостях и пересекает их по прямой. Прямая пересечения имеет следующие особенности:
- Прямая пересечения перпендикулярных плоскостей является прямой линией.
- Прямая пересечения перпендикулярных плоскостей будет перпендикулярна обеим плоскостям.
- Прямая пересечения перпендикулярных плоскостей будет образовывать прямой угол с плоскостями.
Пересечение перпендикулярных плоскостей может вызывать интересные эффекты и свойства. Например, если мы берем две перпендикулярные плоскости и нанизываем на них кольцо, оно будет свободно двигаться по линии пересечения. Это свойство часто используется в механике и конструкции машин.
Таким образом, пересечение перпендикулярных плоскостей представляет собой важное понятие в геометрии и науке. Оно позволяет установить связь между двумя плоскостями и исследовать их взаимодействие.
Перпендикулярные плоскости в трехмерном пространстве
В трехмерном пространстве существуют перпендикулярные плоскости, которые пересекаются под прямым углом. Это означает, что векторы нормалей этих плоскостей ортогональны друг другу.
Перпендикулярность плоскостей имеет важное значение в геометрии, инженерии и физике. Она позволяет определить прямые, лучи и плоскости, а также решать задачи, связанные с нахождением расстояний и координат точек в пространстве.
Условие перпендикулярности
Две плоскости с векторами нормалей n₁ и n₂ перпендикулярны, если их векторы нормалей удовлетворяют условию:
n₁ • n₂ = 0
Пример
Рассмотрим две плоскости в трехмерном пространстве. Пусть у них векторы нормалей равны:
Плоскость 1: n₁ = (1, 2, 3)
Плоскость 2: n₂ = (3, -1, 1)
Чтобы определить, являются ли они перпендикулярными, вычислим их скалярное произведение:
(1, 2, 3) • (3, -1, 1) = 3 — 2 + 3 = 4
Так как полученное значение не равно нулю, плоскости не являются перпендикулярными.
Поэтому, чтобы плоскости были перпендикулярными, скалярное произведение векторов нормалей должно быть равно нулю.
Примеры перпендикулярных плоскостей
Пример 1: Плоскости координатного пространства
В трехмерном координатном пространстве две оси координат – x и y – образуют плоскость xy, а ось z образует перпендикулярную плоскость. Таким образом, плоскость xy и плоскость z являются перпендикулярными.
Пример 2: Плоскости отражения
В оптике, плоскости отражения являются перпендикулярными плоскостям преломления. Например, плоскость зеркала и плоскость преломления при ломании света на границе двух сред образуют перпендикулярные плоскости.
Это лишь некоторые из многочисленных примеров перпендикулярных плоскостей, которые можно встретить в различных сферах науки и техники. Понимание перпендикулярных плоскостей играет важную роль в решении геометрических задач и применении данных понятий в практических задачах.
Перпендикулярные плоскости в геометрии
Перпендикулярные плоскости широко используются в геометрии для решения различных задач. Например, они позволяют определить прямую, перпендикулярную плоскости, провести линию, перпендикулярную другой линии или плоскости, и даже построить геометрические фигуры, такие как прямоугольник или куб.
Важно отметить, что понятие перпендикулярности применяется не только к плоскостям, но и к другим геометрическим объектам, таким как прямые и отрезки. Например, две прямые называются перпендикулярными, если они образуют прямой угол.
Перпендикулярные плоскости играют важную роль в различных областях, включая геометрию, строительство, архитектуру, машиностроение и многое другое. Понимание этого понятия является ключом для решения сложных геометрических задач и создания эффективных конструкций.
Перпендикулярные плоскости в архитектуре
В архитектуре перпендикулярные плоскости играют важную роль, так как они создают визуальный баланс и гармонию в здании. Они используются для создания различных эффектов и акцентов, а также помогают структурировать пространство и делать его более интересным для глаза.
Планирование и организация пространства
Перпендикулярные плоскости в архитектуре часто используются для планирования и организации пространства. Они могут разделять здание на различные функциональные зоны или помогать создать определенную последовательность помещений. При использовании перпендикулярных плоскостей архитекторы могут легко разделить пространство на общественные и частные зоны, например, или создавать переходы между разными областями.
Создание визуальной глубины и перспективы
Перпендикулярные плоскости также помогают создать визуальную глубину и перспективу в архитектурных проектах. Они могут использоваться для создания эффекта глубокой перспективы, когда плоскости расположены под разными углами и создают ощущение движения и простора. Это особенно полезно при создании больших открытых пространств, таких как холлы или фойе, где важно создать впечатление пространственной свободы.
- Использование перекрытий
- Создание фокусных точек
- Усиление архитектурных деталей
Значение перпендикулярных плоскостей в науке

Геометрия
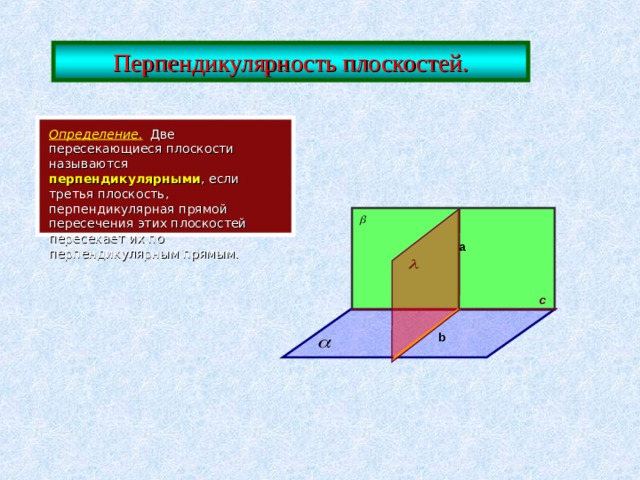
В геометрии перпендикулярные плоскости являются одним из базовых понятий. Они используются для определения прямых, углов и отношений между фигурами. Перпендикулярность играет важнейшую роль в решении различных геометрических задач, например, в построениях и измерениях.
Физика
В физике перпендикулярные плоскости часто встречаются в контексте электромагнетизма. Например, магнитное поле создается перпендикулярно электрическому полю в электромагнитных волнах. Также перпендикулярные плоскости применяются в оптике для описания преломления света и плоской зеркальной поверхности.
Инженерия
В инженерии перпендикулярные плоскости используются для создания 3D-моделей и проекций. Они помогают визуализировать предметы и их отношения в пространстве, что является важным инструментом проектирования и строительства.
Таким образом, перпендикулярные плоскости имеют значительное значение в науке и находят применение в геометрии, физике, инженерии и других областях. Их особенность пересечения под прямым углом делает их удобными инструментами для описания и анализа различных физических и пространственных явлений.
Вопрос-ответ:
Что значит, если две плоскости перпендикулярны?
Если две плоскости перпендикулярны, это значит, что их нормальные векторы ортогональны друг другу.
Какие свойства имеют перпендикулярные плоскости?
Перпендикулярные плоскости имеют следующие свойства: они не пересекаются, не параллельны друг другу и располагаются под прямыми углами друг к другу.
Может ли плоскость быть перпендикулярна самой себе?
Нет, плоскость не может быть перпендикулярна самой себе. Перпендикулярность возникает только между двумя различными плоскостями.
Как найти угол между перпендикулярными плоскостями?
Угол между перпендикулярными плоскостями можно найти с помощью скалярного произведения их нормальных векторов. Угол будет равен арккосинусу от значения скалярного произведения нормальных векторов, деленного на их модули.
Какими свойствами обладают прямая и плоскость, перпендикулярные друг другу?
Прямая и плоскость, перпендикулярные друг другу, обладают следующими свойствами: прямая лежит в плоскости, плоскость пересекает прямую перпендикулярно к ней и эти две фигуры не пересекаются в других точках.
Что такое перпендикулярные плоскости?
Перпендикулярные плоскости — это две плоскости, которые пересекаются под прямым углом.