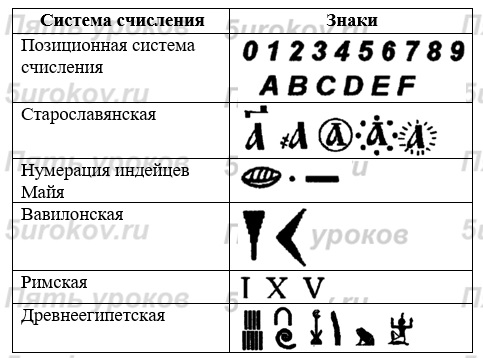
Системы счисления являются неотъемлемой частью нашей повседневной жизни, и мы используем их, даже не задумываясь о том, как они работают. К примеру, наиболее распространена десятичная система счисления с основанием 10.
Однако, помимо десятичной системы, существует множество других позиционных систем счисления с различными основаниями. Именно позиционные системы отличаются своей особенностью – в них значение каждой цифры зависит от ее позиции в числе.
Одной из наиболее распространенных позиционных систем является пятиричная система счисления с основанием 5. Ее особенность заключается в том, что каждая цифра (в данном случае от 0 до 4) имеет свое значение в зависимости от ее местоположения в числе.
Также существуют двенадцатиричная система счисления с основанием 12 и двадцатиричная система с основанием 20. В этих системах также каждая цифра имеет свое значение, но уже в соответствии с их местоположением в числе.
Историческое развитие позиционных систем счисления
Позиционная система счисления с основанием 5
Исторически, одной из самых ранних форм позиционной системы счисления являлась пятеричная система. В этой системе числа представлялись пяти знаками: 0, 1, 2, 3 и 4. Основанием этой системы являлось число 5, и она использовалась в различных древних цивилизациях, включая Майя и Шумеров. Пятеричная система счисления имела свои преимущества, такие как простота использования пальцев для подсчета.
Позиционная система счисления с основанием 10
Основанием десятеричной системы счисления является число 10. Десятичная система счисления стала широко использоваться в большинстве культур в результате использования десяти пальцев на руках. Это основная система счисления, используемая в современной математике и повседневной жизни.
В десятичной системе счисления числа записываются с помощью десяти знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Значение каждой цифры определяется позицией, в которой она находится. Например, число 365 означает 3 * 100 + 6 * 10 + 5 * 1.
Позиционная система счисления с основанием 12 и 20
Помимо пятеричной и десятичной систем счисления, существовали различные другие системы, основанные на различных числах. Некоторые древние культуры использовали двенадцатиричную систему счисления с основанием 12. Эта система имела свои преимущества, такие как легкость деления нацело и использование долей в виде знаков.
Некоторые другие культуры использовали двадцатиричную систему счисления с основанием 20. Эта система также имела свои уникальные особенности, например, использование пальцев на руках и ногах для подсчета.
Важно отметить, что с развитием технологий и математики, десятичная система счисления стала наиболее распространенной и универсальной системой, используемой во многих областях деятельности человека.
Система с основанием 5
Система счисления с основанием 5, также известная как пятеричная система, основана на использовании пяти различных цифр: 0, 1, 2, 3 и 4. В этой системе числа записываются с помощью позиционной нотации, где значение каждой цифры определяется ее позицией в числе.
Позиционная система с основанием 5 имеет много применений, особенно в информатике и математике. Она используется для представления чисел в компьютерах и других устройствах, а также в различных математических задачах.
Основное преимущество пятеричной системы счисления заключается в том, что она позволяет более компактно представлять числа. Ведь в пятеричной системе для записи числа 25 достаточно всего двух цифр — 2 и 0, в то время как в десятичной системе для записи этого числа потребовалось бы две цифры — 2 и 5.
Другое преимущество пятеричной системы заключается в том, что она является более эффективной для решения некоторых математических задач. Например, при работе с некоторыми простыми числами, такими как 5 или его степени, пятеричная система может быть особенно полезной.
И последний, но не менее важный аспект пятеричной системы счисления — это ее использование в некоторых культурах и языках. Некоторые племена и народы использовали пятеричную систему для счета и записи чисел в своих языках и учетных системах.
Система с основанием 10
В десятичной системе счисления каждая цифра имеет свое значение в зависимости от ее позиции. Например, число 237 представляет собой сумму произведений каждой цифры на соответствующую степень числа 10. Таким образом, 237 = 2 * 10^2 + 3 * 10^1 + 7 * 10^0.
Преимущества десятичной системы
Десятичная система позволяет легко понимать и работать с числами в повседневной жизни. Большинство счетчиков и измерительных приборов, таких как часы, термометры, счетчики электроэнергии и т. д., используют десятичную систему для отображения результатов.
Десятичная система также удобна для решения арифметических операций, таких как сложение, вычитание, умножение и деление. Благодаря простоте перевода и манипуляции с десятичными числами, их легко использовать в расчетах, финансах и других областях.
Десятичная система и компьютеры
Десятичная система не является прямым представлением внутреннего хранения чисел в компьютерах, где применяется двоичная система счисления. Однако десятичные числа могут быть легко преобразованы в двоичные числа, чтобы быть обработанными компьютерами, и наоборот.
Несмотря на то, что в компьютерах используется двоичная система счисления, десятичная система все еще широко применяется при отображении результатов в программах и взаимодействии с пользователем.
Десятичная система счисления является наиболее распространенной и удобной системой для повседневного использования и выполнения арифметических операций. Она позволяет нам легко понимать и работать с числами в нашей современной жизни.
Система с основанием 12
Система счисления с основанием 12 известна как дуо-десятеричная система. Отличается тем, что она использует 12 различных цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А и В.
Использование основания 12 позволяет представлять числа более компактно по сравнению с десятичной системой счисления. Кроме того, система с основанием 12 обладает особыми свойствами, которые делают ее удобной для определенных вычислений. Например, в системе с основанием 12 удобно делить на 2, 3, 4 и 6, так как числа 2, 3, 4 и 6 без остатка делятся на 12.
Система с основанием 12 также имеет свои особенности в отношении записи десятичных дробей. В ней используется специальный символ «11» для обозначения 1/12, «12» для обозначения 1/144 и т. д.
Дуо-десятеричная система счисления имеет широкое применение в различных областях, например, в измерении времени (часы и минуты), угловых градусах и минутах дуги, а также в музыкальной нотации.
Система с основанием 20
В системе с основанием 20 используются цифры от 0 до 9 и буквы от A до J для обозначения десятой, одиннадцатой, двенадцатой и так далее позиций в числе. Например, число 21 в системе с основанием 20 записывается как 1A, число 100 — как 50, а число 1000 — как 4E0. Позиция крайней правой цифры в числе равна 0, следующей за ней — 1, за ней — 2 и так далее.
Примеры выполнения операций в системе с основанием 20:
- Сложение: для сложения двух чисел в системе с основанием 20 необходимо сложить соответствующие цифры, учитывая переносы при необходимости.
- Вычитание: для выполнения вычитания двух чисел в системе с основанием 20 необходимо вычесть соответствующие цифры, учитывая нужные заемы при необходимости.
- Умножение: для умножения числа в системе с основанием 20 на множитель, необходимо умножить каждую цифру числа на множитель и сложить полученные результаты с учетом позиций.
- Деление: для деления числа в системе с основанием 20 на делитель, необходимо подобно умножению повторять вычитание множителя из делимого, пока делимое не станет меньше делителя.
Система с основанием 20 имеет свои преимущества и недостатки. Одним из преимуществ является возможность компактного представления больших чисел с помощью меньшего количества цифр. Однако, для работы с такой системой необходимо использовать специальное оборудование или программное обеспечение для перевода чисел из системы с основанием 20 в десятичную систему счисления и обратно. Кроме того, сложность выполнения арифметических операций в такой системе может быть выше, чем в десятичной системе.
Как работает позиционная система счисления
Основание системы счисления определяет количество различных цифр, которые можно использовать для записи чисел. Например, в десятичной системе счисления (основание 10) мы используем цифры от 0 до 9.
В позиционной системе счисления каждая позиция имеет свой вес, который равен основанию системы, возведенному в степень позиции. Например, в десятичной системе число 1234 можно представить как 1 * 10^3 + 2 * 10^2 + 3 * 10^1 + 4 * 10^0.
Позиционная система счисления позволяет нам записывать числа любого значения, используя ограниченное количество цифр и позиций. Каждая цифра в числе представляет определенное количество, умноженное на вес своей позиции.
Примеры позиционных систем счисления:
1. В пятеричной системе счисления (основание 5) мы используем цифры от 0 до 4. Например, число 42 в пятеричной системе можно представить как 4 * 5^1 + 2 * 5^0.
2. В двоичной системе счисления (основание 2) мы используем только две цифры: 0 и 1. Например, число 101 в двоичной системе можно представить как 1 * 2^2 + 0 * 2^1 + 1 * 2^0.
Один из примеров позиционных систем счисления это десятичная система счисления, которую мы обычно используем в повседневной жизни.
В позиционной системе счисления легко производить арифметические операции, такие как сложение, вычитание, умножение и деление. Каждая операция выполняется над цифрами в соответствующей позиции и весе. Например, при сложении двух чисел мы складываем цифры одной позиции и переносим единицу в следующую позицию, если сумма превышает основание системы.
Позиционные системы счисления облегчают запись и обработку чисел, позволяя нам работать с большими числами и различными системами счисления в рамках одной математической модели.
Почему системы с разными основаниями называются позиционными

Системы с разными основаниями называются позиционными, потому что положение цифры в числе имеет значение. Например, в десятичной системе значение цифры зависит от того, в каком разряде она находится. Цифра 2 в разряде единиц означает две единицы, а в разряде десятков — двадцать.
Таким образом, основание системы счисления определяет количество различных цифр, которыми можно представить число. Например, в двоичной системе счисления с основанием 2 можно использовать только две цифры 0 и 1.
Использование разных оснований позволяет выбрать оптимальный способ представления чисел в зависимости от конкретных нужд. Например, в шестнадцатеричной системе счисления с основанием 16 используются цифры от 0 до 9 и буквы от A до F, что позволяет более компактно записывать большие числа в сравнении с десятичной системой.
Применение позиционных систем счисления в современной математике
Применение позиционных систем счисления с основаниями 5, 10, 12 и 20 в современной математике широко используется в различных областях, включая финансы, экономику, физику, компьютерные науки и др.
Одно из важных применений позиционных систем счисления — это представление чисел в компьютерных системах. Компьютеры используют двоичную (основание 2) позиционную систему счисления, в которой каждая позиция числа имеет вес, равный степени двойки. Это позволяет компьютерам представлять и обрабатывать информацию в виде двоичных чисел, что обеспечивает высокую эффективность и точность вычислений.
Позиционная система счисления также широко применяется в финансовой математике для расчетов процентных ставок, дисконтирования и сравнения различных финансовых инструментов. В данном случае, основание системы счисления имеет значение для точности и эффективности расчетов.
Еще одним применением позиционных систем счисления является использование их в криптографии. Криптографические алгоритмы часто требуют манипуляций с числами большой длины, которые превышают размерность типов данных, используемых в языках программирования. Позиционные системы счисления с большими основаниями (например, 20) позволяют представлять такие числа эффективно и компактно, что является важным фактором в криптографии.
Таким образом, применение позиционных систем счисления с различными основаниями в современной математике находит широкое применение в разных областях, обеспечивая эффективность и точность вычислений, а также компактность представления чисел.
Вопрос-ответ:
Какие основания систем счисления называют системами?
Основания систем счисления 5, 10, 12 и 20 называют системами, потому что они основаны на определенных числах, которые используются для представления всех чисел в этих системах.
Почему системы счисления с основаниями 5, 10, 12 и 20 являются позиционными?
Системы счисления с основаниями 5, 10, 12 и 20 являются позиционными, потому что значение каждой позиции в числе определяется основанием системы.
Какие основания систем счисления используются в нашей повседневной жизни?
В повседневной жизни мы обычно используем двоичную систему счисления (основание 2), десятичную систему счисления (основание 10) и шестнадцатеричную систему счисления (основание 16).
Почему основание 10 является широко используемым в системах счисления?
Основание 10 является широко используемым в системах счисления, потому что оно соответствует количеству пальцев на руках человека, что делает его удобным для повседневных расчетов.