
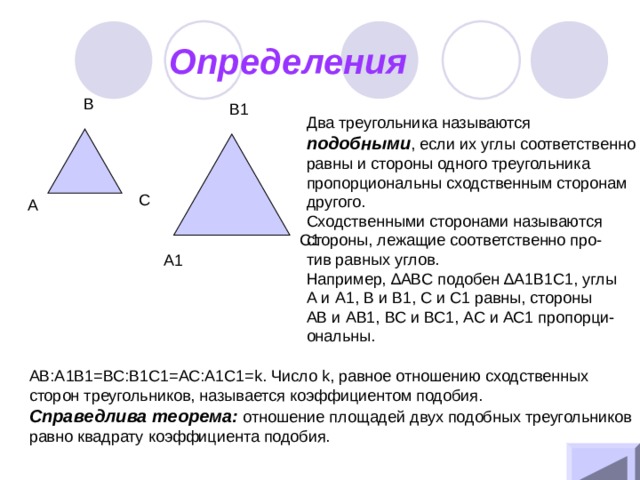
В геометрии школьной программы 8 класса особое внимание уделяется понятию подобия треугольников. Подобные треугольники – это фигуры, которые имеют равные соответствующие углы. Они не только похожи на друг друга, но и сохраняют пропорциональность длин сторон. Важно понимать, что подобные треугольники не являются равными, так как могут иметь разную величину сторон.
Для определения подобных треугольников используется несколько признаков. Если соответствующие углы двух треугольников равны, то они будут подобными. Кроме того, треугольники могут быть подобными, если у них соответствующие стороны пропорциональны. Например, если для двух треугольников выполнено условие, что отношение длины одной стороны к длине соответствующей стороны другого треугольника всегда равно одному и тому же числу, то они будут подобными.
Подобные треугольники играют важную роль не только в геометрии, но и в других областях науки и техники. Знание и понимание понятия подобия помогает в решении задач, связанных с определением пропорциональности, масштабированием и упрощением фигур. Одной из наиболее практически полезных областей подобных треугольников является строительство и архитектура, где требуется определение пропорциональности объектов и разработка масштабных чертежей.
Определение подобных треугольников
Для двух треугольников ABC и DEF справедливо следующее условие подобия:
ABC подобен DEF, если:
- Величины соответствующих углов равны;
- Длины соответствующих сторон образуют пропорцию:
AB/DE = BC/EF = AC/DF
Такое условие гарантирует подобие треугольников, так как пропорциональные стороны в сочетании с равными углами определяют подобие.
Подобные треугольники имеют схожие свойства, которые можно использовать для решения задач. Например, если ты знаешь длины сторон одного треугольника и его углы, то с помощью подобия можешь вычислить длины сторон и углы другого подобного треугольника.
Свойства подобных треугольников широко применяются в геометрии и других науках, где необходимо работать с подобными фигурами и их характеристиками.
Подобные треугольники: основные определения
Основное определение подобных треугольников заключается в следующем:
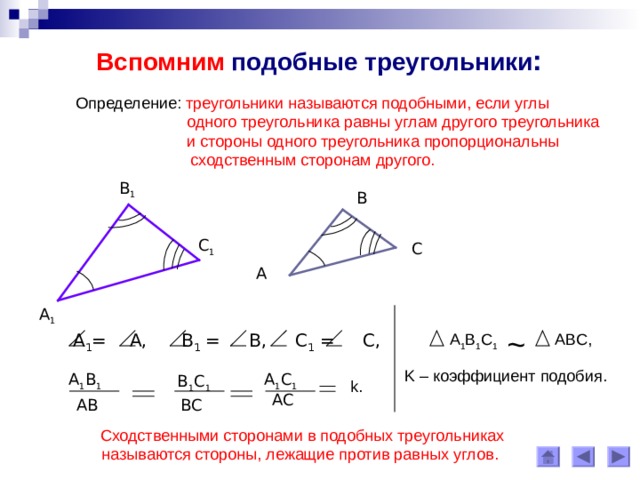
Подобными называются треугольники, если углы одного треугольника равны соответствующим углам другого треугольника.
Важно отметить, что признак подобия треугольников справедлив только в том случае, если соответствующие углы равны, а стороны пропорциональны. Просто равные треугольники считаются подобными, но это не является достаточным условием для подобия треугольников.
Подобные треугольники имеют несколько свойств:
- Соответствующие углы равны: угол α первого треугольника равен углу α второго треугольника, угол β первого треугольника равен углу β второго треугольника и угол γ первого треугольника равен углу γ второго треугольника.
- Соответствующие стороны пропорциональны: отношение длин сторон первого треугольника к длине соответствующих сторон второго треугольника одинаково для всех сторон.
Значение подобия треугольников заключается в возможности рассчитать длины сторон и измерить углы треугольника, основываясь на известных данных о другом треугольнике. Также подобные треугольники используются в геометрии для построения фигур и решения задач.
Критерии подобия треугольников
Критерий AA
Если два треугольника имеют два равных угла, то они подобны друг другу. Этот критерий называется критерием «угол-угол» (AA).
Критерий Подобия с учетом соотношения сторон
Если два треугольника имеют соответствующие стороны в пропорции, то они подобны друг другу. Этот критерий называется критерием «пропорциональность сторон».
Например, если в треугольнике АВС и треугольнике DEF стороны AB и DE, BC и EF, AC и DF имеют одно и то же отношение, то АВС и DEF подобны друг другу.
Критерии подобия треугольников служат основой для решения различных задач и вычислений в геометрии. Правильное применение критериев позволяет не только установить подобие треугольников, но и решить задачи на нахождение отсутствующих сторон и углов.
Измерение подобия треугольников
Для измерения подобия треугольников используется отношение длин соответствующих сторон. Если в двух треугольниках соответствующие стороны имеют одинаковые отношения (то есть их длины пропорциональны), то эти треугольники называются подобными.
Отношение длин соответствующих сторон можно выразить с помощью коэффициента подобия, который равен отношению длины одной стороны одного треугольника к длине соответствующей стороны другого треугольника.
Для того чтобы проверить подобие треугольников, необходимо убедиться, что все соответствующие углы равны, а также вычислить отношение длин соответствующих сторон и проверить, что оно равно коэффициенту подобия.
Если треугольники подобны, то их соответствующие углы равны, а отношение длин соответствующих сторон будет постоянным и равным коэффициенту подобия.
Изучение подобия треугольников позволяет решать множество задач в геометрии, например, вычислять недостающие значения сторон или углов треугольников, определять расстояния и масштабы на картах и планах, а также строить аналогии и анализировать геометрические формы.
Теорема о подобии треугольников
Треугольники называются подобными, если у них соответственные углы равны. Обозначается это как «АВС ∼ ХУZ», где ∼ означает «подобный».
Основная теорема о подобии треугольников утверждает, что если у двух треугольников соответственные углы равны, то соответственные стороны этих треугольников пропорциональны.
Таким образом, если АВС ∼ ХУZ, то:
| AB/ХУ = BC/УZ = AC/ХZ |
Это означает, что если два треугольника подобны, то отношения длин соответственных сторон этих треугольников равны.
Теорема о подобии треугольников широко используется в геометрии для решения задач, связанных с построением и вычислением неизвестных величин.
Также важно отметить, что в случае подобных треугольников соответствующие углы соответственно равны, но это не означает, что треугольники равны. Равные треугольники подобны, но подобные не всегда равны.
Решение задач по подобным треугольникам
Алгоритм решения задач по подобным треугольникам:
1. Необходимо определить, являются ли заданные треугольники подобными. Для этого достаточно проверить, что их соответствующие стороны пропорциональны, то есть отношение длин сторон одного треугольника к длинам соответствующих сторон другого треугольника одинаково для всех трех пар сторон.
2. Если треугольники подобны, то можно использовать соответствующие свойства для решения задачи. Например, если известны длины двух сторон подобных треугольников, можно найти длины оставшихся сторон, используя пропорциональность.
3. Используя свойство равенства соответствующих углов, можно найти значения углов заданных треугольников.
4. Решение задачи может также требовать вычисления площадей подобных треугольников. Если треугольники подобны, то отношение площадей этих треугольников равно квадрату отношения длин соответствующих сторон.
5. При решении задачи по подобным треугольникам необходимо учесть, что подобные треугольники могут быть сдвинуты, повернуты или зеркально отражены друг относительно друга, но они все равно будут являться подобными.
Важно помнить, что решение задач по подобным треугольникам требует внимательности и точности. Необходимо аккуратно производить все вычисления и проверять полученные результаты на соответствие условию задачи.
Пример:
Задача: В треугольнике ABC проведена высота AH. Найдите высоту BK треугольника ABK, если AB и AK образуют прямой угол.
Решение:
Треугольники AHB и ABK подобны, так как у них углы АBН и АКB прямые, следовательно, треугольники обладают одним прямым углом и имеют одинаковый угол А. Треугольники также имеют общую сторону AB.
Поэтому, мы можем записать следующее:
AB/АK = AH/BK
Или:
АK = AB * BK / AH
Зная значения сторон AB и AH, мы можем вычислить значение высоты BK треугольника ABK, используя пропорцию.
Таким образом, зная свойства подобных треугольников и умея применять их при решении задач, можно эффективно решать геометрические задачи, связанные с подобными треугольниками.
Применение подобных треугольников в геометрии
Подобные треугольники в геометрии широко применяются для решения различных задач. Когда треугольники подобны, это означает, что их соответствующие углы равны, а соответствующие стороны пропорциональны.
Нахождение пропорциональных сторон
Нахождение высот и площадей
Другим важным применением подобных треугольников является нахождение высот и площадей. Если два треугольника подобны, то соответствующие стороны их высот также являются пропорциональными. Это позволяет находить высоту одного треугольника зная высоту другого. Кроме того, площади подобных треугольников связаны квадратичной зависимостью. Если стороны двух треугольников имеют отношение k, то площадь одного треугольника будет k^2 раз больше площади другого треугольника.
Практические примеры подобных треугольников
Знание и понимание подобия треугольников на практике помогает решать разнообразные задачи, связанные с нахождением неизвестных сторон и углов треугольников.
Пример 1: Схожие треугольники в строительстве
В строительстве подобные треугольники широко используются для определения высоты объектов и построения более точных планов. Например, с помощью подобия треугольников можно определить высоту высокого здания, измеряя его тень и тень более низкого объекта в одно и то же время.
Пример 2: Упрощение задач на нахождение долей отрезков
Подобные треугольники также могут быть полезны при решении задач на нахождение долей отрезков. Например, если известно, что два треугольника подобные, то отношение длин соответствующих сторон будет одинаковым. Используя это свойство, можно находить доли отрезков внутри треугольника и сравнивать их.
Важно понимать, что для применения подобия треугольников, достаточно знания соответствующих пар сторон и углов. При этом треугольники не обязательно должны быть равнобедренными или прямоугольными.
Запомните: подобные треугольники имеют пропорциональные стороны и равные соответствующие углы!
Вопрос-ответ:
Как определить, что два треугольника подобны?
Два треугольника считаются подобными, если у них соответствующие углы равны, а соотношение длин их сторон одинаково.
Как вычислить коэффициент подобия треугольников?
Коэффициент подобия двух треугольников можно вычислить, сравнивая длины соответствующих сторон. Коэффициент равен отношению длины одной стороны одного треугольника к длине соответствующей стороны другого треугольника.
В чем особенность подобных треугольников?
Особенностью подобных треугольников является то, что они имеют одинаковую форму, но могут быть разных размеров. То есть, подобные треугольники имеют равные углы, но могут иметь разные длины сторон.
Как можно узнать, что треугольники подобны по геометрическим признакам?
У треугольников есть несколько геометрических признаков, которые позволяют определить их подобие. Самый простой признак — равные углы. Если все углы одного треугольника равны соответствующим углам другого треугольника, то они подобны. Также можно смотреть на отношение длин сторон треугольников.
На что нужно обратить внимание при решении задач на подобные треугольники?
При решении задач на подобные треугольники важно обратить внимание на равные углы и отношения длин сторон. Их нужно правильно использовать для нахождения неизвестных величин или для установления связей между различными сторонами и углами треугольников.
Что такое подобные треугольники?
Подобные треугольники — это треугольники, у которых соответствующие углы равны, а соответствующие стороны пропорциональны.
Как проверить, что треугольники являются подобными?
Для проверки подобия треугольников необходимо проверить, что у них соответствующие углы равны и что соответствующие стороны пропорциональны.