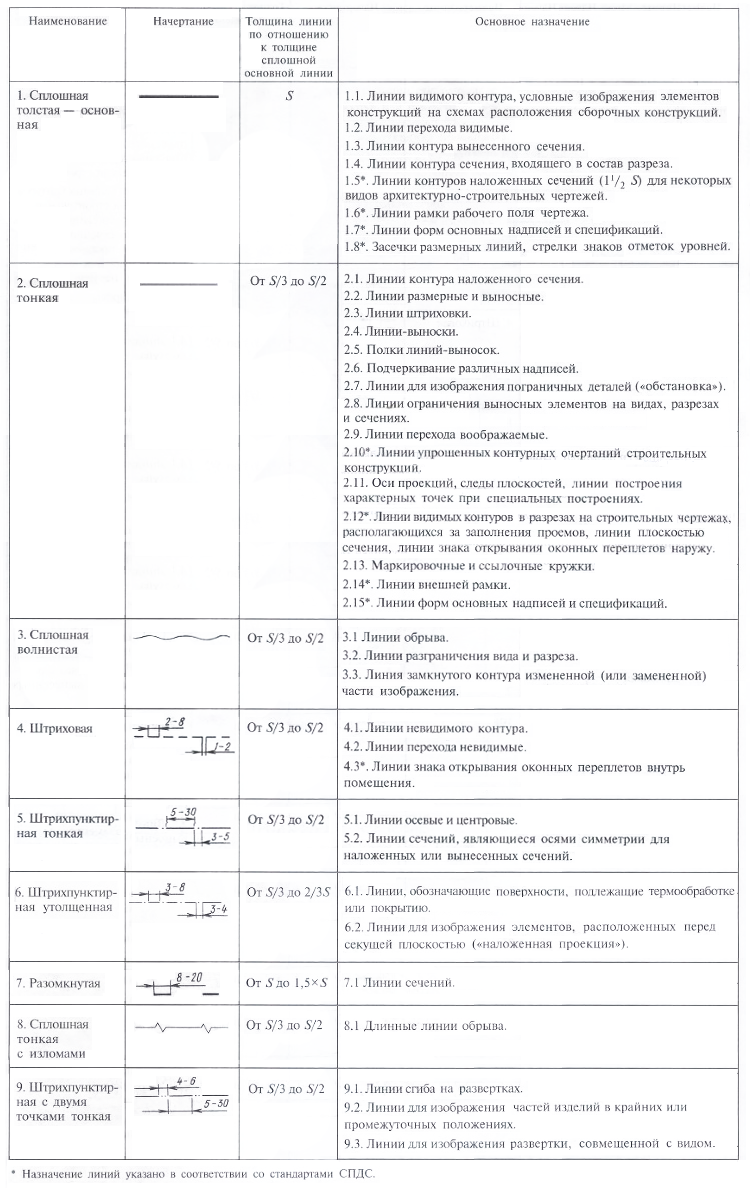
Линия является одной из самых простых геометрических фигур. Она представляет собой набор бесконечно малых точек, расположенных вдоль одной прямой. В единичной системе координат линия может быть задана уравнением вида y = kx + b, где k — коэффициент наклона, а b — коэффициент смещения по оси OY.
В зависимости от своего положения и направления линии могут называться по-разному. Так, горизонтальная линия представляет собой линию, расположенную параллельно оси OX и имеющую нулевой коэффициент наклона (k = 0). В то же время, вертикальная линия проходит параллельно оси OY и не имеет определенного угла наклона.
Линии также могут быть наклонными или диагональными. Наклонная линия имеет ненулевой коэффициент наклона, а диагональная линия располагается в пространстве, не параллельно ни одной из осей координат. Она проходит под углом к оси OX и оси OY и имеет несимметричный вид.
Определение линии в геометрии
Линия не имеет начала или конца, и она представляет собой абстрактное понятие, которое нельзя изобразить и построить в реальности.
Линии имеют различные свойства и классифицируются по их форме и положению. Например, прямые линии не имеют изгибов, в то время как кривые линии могут быть изогнутыми или закругленными. Также линии могут быть параллельными или пересекаться друг с другом.
Основные свойства линий:
Протяженность: линия является объектом нулевой толщины и простирается вдоль бесконечной прямой.
Прямизна: прямая линия не имеет изгибов или изломов и может быть нарисована с помощью двух точек.
Линии являются важной частью геометрии и используются для построения фигур, измерения расстояний и решения различных задач.
Понятие линии
Линии играют важную роль в художественном и графическом искусстве, а также в разных областях дизайна и архитектуры. Они могут быть горизонтальными, вертикальными или наклонными, прямыми или кривыми, сплошными или прерывистыми.
Линии могут также передавать разные эмоциональные и символические значения. Например, прямые линии часто ассоциируются с силой и уверенностью, кривые линии – с гибкостью и плавностью.
Линии также используются для создания разных визуальных эффектов, таких как текстуры, контуры и перспектива. Они могут быть использованы для обозначения границ, направления движения, центральных осей и многое другое.
В современном мире линии стали неотъемлемой частью дизайна интерфейсов, сайтов и логотипов. Они помогают создавать упорядоченность и структуру, а также визуально подчеркивают важные элементы.
Важно отметить, что линии бывают не только визуальными, но и абстрактными. Например, математические функции и уравнения также могут быть представлены в виде линий.
Типы линий
Линии играют важную роль в дизайне и графике. Они могут быть использованы для создания различных эффектов, указания направления, разделения элементов или просто добавления декоративных элементов.
Прямые линии
Прямая линия — это линия, которая не имеет изгибов или изломов. Она может быть горизонтальной или вертикальной, создавая четкие и прямые направления. Прямые линии часто используются для разделения различных частей дизайна или для создания рамок.
Изогнутые линии
Изогнутая линия — это линия, которая имеет изгибы или изломы. Она создает более органический и плавный вид и может использоваться для создания кривых форм и волновых эффектов. Изогнутые линии могут добавлять движение и интерес к дизайну.
Свойства линий
В веб-разработке существует несколько свойств, которые позволяют контролировать внешний вид линий на веб-странице. Рассмотрим некоторые из них:
Толщина линии: используя свойство border-width, можно задать толщину линии. Значение указывается в пикселях.
Стиль линии: свойство border-style позволяет выбрать стиль линии. Некоторые из возможных значений — solid (сплошная), dotted (точечная), dashed (пунктирная).
Цвет линии: с помощью свойства border-color, можно задать цвет линии. Значение может быть указано в разных форматах — названием цвета (например, red) или в шестнадцатеричном формате (#FF0000).
Закругление углов: свойство border-radius позволяет изменять форму углов линии, указывая радиус скругления. Значение указывается в пикселях или процентах.
Тень линии: с помощью свойства box-shadow можно создавать тень для линии. Значение свойства задается в формате h-shadow v-shadow blur color, где h-shadow и v-shadow определяют смещение тени по горизонтали и вертикали, blur — размер размытия тени, а color — цвет тени.
Это лишь некоторые из свойств, которые можно использовать для создания и настройки линий на веб-странице. Комбинируя эти свойства, можно добиться разнообразных эффектов и дизайнов.
Прямая и кривая линия
В математике существует два вида линий: прямая и кривая. Они имеют различные свойства и используются в разных областях знаний.
Прямая линия
Прямая линия — это наиболее простой вид линии, отличающийся отсутствием изгибов и поворотов. Она обладает следующими характеристиками:
- Прямая линия простирается в бесконечность в обе стороны, не имея конечных точек.
- На прямой линии можно выбрать любые две точки, и они всегда будут находиться на этой линии.
- Прямая линия не имеет ширины, она представляет собой одномерный объект.
Прямые линии широко применяются в геометрии, инженерии и физике. Они используются для измерений, моделирования и построения графиков.
Кривая линия
Кривая линия — это линия с изгибами и различными формами. Кривые линии могут быть описаны с помощью различных математических функций, уравнений или заданных точек. Основные характеристики кривой линии:
- Кривая линия имеет определенное начало и конец.
- На кривой линии можно выбрать любые две точки, и они будут находиться на этой линии, но не на всех ее участках.
- Кривая линия может иметь разную форму и изгибы, включая спирали, окружности и эллипсы.
Кривые линии широко используются в геометрии, физике, компьютерной графике, медицинском моделировании и других областях, где требуется описание сложных форм и движений.
Пересечение линий
Пересечение линий имеет важное значение в решении множества задач и проблем. Например, они используются для нахождения точек пересечения дорог, строительства, определения положения объектов на плоскости и многое другое.
При решении задачи о пересечении линий необходимо учитывать различные факторы, такие как угол наклона линий, их длина, тип их кривизны и другие. Для определения точки пересечения часто используют методы аналитической геометрии, включающие в себя системы уравнений или определение координат точки.
Пересечение линий может иметь разные результаты: линии могут пересекаться в одной точке, параллельны или не пересекаться вовсе. Понимание этих результатов очень важно при решении задачи или проблемы.
Важно отметить, что пересечение линий может быть не только в двухмерном пространстве, но и в трехмерном и других размерностях. В каждой размерности пересечение линий будет иметь свои особенности и методы решения.
Ломаная и замкнутая ломаная
Ломаная
Ломаная — это линия, состоящая из последовательности отрезков, соединяющих последовательные точки на плоскости. Каждый отрезок называется стороной ломаной, а точки, которые являются концами этих отрезков, называются вершинами. Между любыми двумя соседними точками может быть одна или несколько прямых частей, которые образуют углы.
Ломаная может быть разной формы и иметь разное количество сторон. Например, ломаная может быть открытой — иметь только начальную и конечную точку, также она может быть замкнутой — начальная и конечная точки совпадают.
Ломаная может использоваться для визуализации различных объектов, например, пространственных форм, кругового движения, временных изменений и т. д. Она может быть также использована для анализа свойств и отношений между точками и отрезками в геометрических задачах.
Замкнутая ломаная
Замкнутая ломаная — это ломаная, у которой начальная и конечная точки совпадают, то есть последняя точка соединена с первой точкой. Иначе говоря, это линия, которая образует замкнутый контур или фигуру.
Замкнутые ломаные широко используются в геометрии для визуализации и анализа множества различных фигур, таких как круги, эллипсы, многоугольники и т. д. Они также могут использоваться для определения их свойств, например, вычисления площади или периметра.
Важно отметить, что замкнутая ломаная может быть аппроксимацией окружности или другой фигуры и может иметь различную степень сложности и точность.
Отрезок и полуотрезок
Полуотрезок — это участок прямой, который ограничен одной точкой. Он имеет начало или конец, который называется концом полуотрезка.
Окончательное определение отрезка и полуотрезка можно привести с помощью формулы:
Отрезок
Отрезок [A, B] представляет собой множество точек на прямой, лежащих между A и B, а также самые точки A и B:
[A, B] = x , где A и B — концы отрезка, x — точка на отрезке.
Полуотрезок
Полуотрезок AB представляет собой множество точек на прямой, лежащих либо слева, либо справа от точки A, включая саму точку A:
AB = x , где A — начало полуотрезка, x — точка на полуотрезке.
Прямая и косая линия
Косая линия — это линия, которая не является прямой и имеет изгибы или изломы. Она может быть нарисована между двумя точками с изменением направления. Косые линии используются для создания сложных форм и фигур, они могут быть кривыми, зигзагообразными или иметь другие характерные изгибы.
Прямые и косые линии играют важную роль в графическом дизайне, искусстве и архитектуре. Они могут передавать различные эмоции и ощущения, а также использоваться для создания гармоничных композиций и эффектных образов.
Вопрос-ответ:
Что такое линия?
Линия – это геометрическая фигура, которая представляет собой бесконечную прямую или кривую.
Какие бывают типы линий?
Существует несколько типов линий, например, прямая линия, кривая линия, вертикальная линия, горизонтальная линия, диагональная линия и т.д.
Как линии используются в различных областях?
Линии используются в различных областях, например, в геометрии, графике, архитектуре, дизайне, искусстве и т.д. Они могут быть использованы для создания форм, разделения пространства, создания рисунков и т.п.
Как называются отрезки линий?
Отрезки линий называются сегментами. Они могут быть прямыми сегментами, кривыми сегментами или комбинацией обоих.