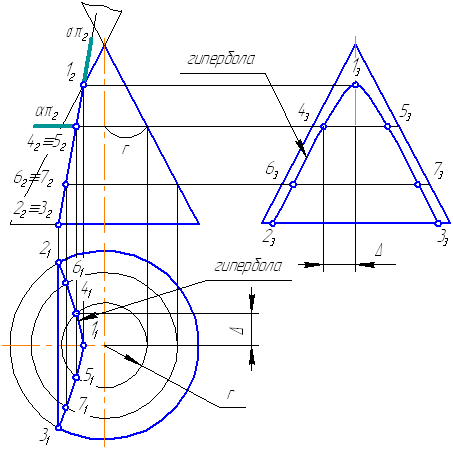
При пересечении поверхности с плоскостью может образоваться различное количество и форма фигур. Однако, существуют основные классы фигур, которые получаются при этом процессе. Одной из таких фигур является пересечение эллипсоида и плоскости.
Эллипсоид — это трехмерная геометрическая фигура, которая имеет форму эллипсоида вращения. Когда плоскость пересекает эллипсоид, в результате получается эллипс. Эллипс обладает некоторыми уникальными свойствами, например, все его точки, сумма расстояний от которых до двух заданных точек — фокусов, одинакова.
Вторым примером является пересечение цилиндра и плоскости. Цилиндр — это трехмерная геометрическая фигура, образованная при вращении прямоугольника вокруг одной из его сторон. При пересечении плоскостью, проходящей через цилиндр, может получиться как эллипс, так и окружность. В случае, если плоскость проходит через ось цилиндра, пересечение будет представлять одну точку.
Кроме эллипса и окружности, при пересечении поверхности с плоскостью могут образоваться более сложные фигуры, такие как гипербола, парабола или плоская кривая. Все эти фигуры изучаются в математике и имеют важные приложения в различных областях науки и техники.
Фигуры, получаемые при пересечении поверхностей с плоскостью
Если поверхность имеет форму плоскости и плоскость пересекает ее, то получится отрезок. В этом случае фигура будет иметь форму прямолинейного сегмента.
При пересечении сферой плоскостью можно получить различные фигуры. Если плоскость пересекает сферу через ее центр, то получится круг. Если плоскость пересекает сферу не через центр, то получится эллипс.
Если плоскость пересекает конус, то возможны три варианта: если плоскость проходит через вершину конуса, то получится точка; если плоскость проходит по базе конуса, то получится многоугольник; если плоскость проходит ни через вершину, ни по базе, то получится часть плоского эллиптического конуса. В зависимости от угла наклона плоскости конуса, фигура может иметь различные формы.
Прямая, пересекающая цилиндр параллельно его оси, образует параллельные отрезки. Если прямая пересекает цилиндр в одном из боковых образующих, то получится эллипс. Если прямая проходит перпендикулярно образующей и не проходит через ее начало, то получится окружность.
В итоге, фигуры, получаемые при пересечении поверхностей с плоскостью, могут иметь самые разнообразные формы, в зависимости от формы поверхности и угла плоскости.
Какой результат возникает?
При пересечении поверхности с плоскостью может возникнуть различные результаты, в зависимости от взаимного расположения поверхности и плоскости.
Если плоскость пересекает поверхность в точке, то результатом будет точка.
Если плоскость пересекает поверхность по прямой, то результатом будет прямая.
Если плоскость пересекает поверхность по кривой, то результатом будет кривая.
Если плоскость пересекает поверхность по многоугольнику или кругу, то результатом будет многоугольник или круг соответственно.
Если плоскость параллельна поверхности и пересекает ее, то результатом будет пустое множество или параллельные прямые.
Если плоскость не пересекает поверхность, то результатом будет пустое множество.
Таким образом, результат пересечения поверхности с плоскостью может быть точкой, прямой, кривой, многоугольником, кругом или пустым множеством.
| Результат | Описание |
|---|---|
| Точка | Пересечение в точке |
| Прямая | Пересечение по прямой |
| Кривая | Пересечение по кривой |
| Многоугольник | Пересечение по многоугольнику |
| Круг | Пересечение по кругу |
| Пустое множество | Нет пересечения |
Понятие фигуры пересечения
Фигура пересечения может иметь разные формы и размеры в зависимости от формы и положения объектов, которые пересекаются. Например, если плоскость пересекает шар, фигура пересечения будет кругом. Если плоскость пересекает куб, фигура пересечения будет шестигранником.
Фигуры пересечения широко используются в геометрии, инженерии и других областях. Они позволяют анализировать и визуализировать взаимодействие между объектами, а также находить точки пересечения и расчеты площади и объема фигур.
Изучение фигур пересечения помогает понять свойства и характеристики различных геометрических объектов и решать сложные проблемы, связанные с их взаимодействием.
Примеры фигур пересечения
При пересечении поверхности с плоскостью могут образовываться различные фигуры. Рассмотрим несколько примеров:
- Окружность — при пересечении сферы плоскостью получается окружность, образованная всеми точками сферы, лежащими в плоскости.
- Эллипс — при пересечении эллипсоида плоскостью получается эллипс, который можно описать как ограниченную кривую.
- Прямая — при пересечении цилиндра, параллельного поверхности, плоскостью получается прямая, которая содержит все точки на границе цилиндра.
- Полигон — при пересечении многогранника плоскостью образуется полигон, который может быть треугольником, прямоугольником или другой многоугольной фигурой, в зависимости от формы многогранника.
- Закрытая кривая — при пересечении тора плоскостью получается закрытая кривая, например окружность или эллипс.
Это лишь некоторые примеры фигур, которые могут образовываться при пересечении поверхности с плоскостью. В зависимости от формы поверхности и плоскости, фигура пересечения может быть разной. Важно отметить, что пересечение поверхности с плоскостью происходит в трехмерном пространстве, однако для удобства рассмотрения примеров мы ограничимся двумерной плоскостью.
Какие фигуры можно получить?
При пересечении поверхности с плоскостью можно получить различные геометрические фигуры, в зависимости от формы и расположения поверхности:
- Окружность — если плоскость пересекает поверхность, образуя замкнутую кривую без самопересечений.
- Эллипс — если плоскость пересекает поверхность, образуя овальную кривую.
- Прямоугольник — если плоскость пересекает поверхность, образуя четырехугольник с прямыми углами.
- Треугольник — если плоскость пересекает поверхность, образуя трехугольник.
- Многоугольник — если плоскость пересекает поверхность, образуя фигуру с более чем тремя сторонами.
- Неопределенная фигура — если плоскость пересекает поверхность в нескольких местах, образуя сложную кривую фигуру без явно определенной формы.
Таким образом, при пересечении поверхности с плоскостью можно получить разнообразные фигуры, которые могут быть полезными при изучении геометрии и анализе формы и структуры поверхностей.
Плоская фигура
Плоские фигуры широко используются в геометрии. Они могут быть классифицированы на основе своей формы. Некоторые из наиболее распространенных плоских фигур включают треугольник, квадрат, прямоугольник, круг, эллипс, ромб, параллелограмм и многоугольник.
Каждая плоская фигура имеет свои уникальные свойства и характеристики. Например, треугольник описывается тремя сторонами и тремя углами, в то время как круг характеризуется радиусом и диаметром. От этих свойств зависят конкретные правила и формулы, используемые при решении задач и вычислениях, связанных с этими фигурами.
Изучение плоских фигур важно для понимания и применения геометрических принципов в различных научных и практических областях. Плоские фигуры могут быть использованы для моделирования и решения задач, связанных с площадью, периметром, объемом и другими параметрами, что делает их неотъемлемой частью образования в области математики и естественных наук.
Телесная фигура
Одной из основных характеристик телесной фигуры является ее поверхность. При пересечении поверхности телесной фигуры с плоскостью может образоваться новая фигура, которая называется сечением.
Сечение может иметь различную форму и свойства в зависимости от положения плоскости относительно телесной фигуры. Например, если плоскость пересекает цилиндр параллельно его основанию, то сечение будет кругом. Если плоскость пересекает цилиндр под наклоном, то сечение будет эллипсом или многогранником.
Сечение телесной фигуры может быть использовано для определения ее формы, площади, объема и других характеристик. Также сечение может служить визуальным примером, позволяющим представить форму телесной фигуры на плоскости.
Телесные фигуры являются основой для изучения геометрии и применяются в различных науках и областях, таких как архитектура, инженерия, физика и дизайн.
| Название телесной фигуры | Описание |
|---|---|
| Параллелепипед | Тело, у которого все грани параллельны и одинаковой формы |
| Сфера | Тело, все точки которого равноудалены от центра |
| Конус | Тело, у которого одна из поверхностей является окружностью |
| Цилиндр | Тело, у которого две поверхности являются окружностями параллельными оси |
Какие свойства имеют такие фигуры?
Фигуры, получаемые при пересечении поверхности с плоскостью, имеют ряд уникальных свойств.
Во-первых, данные фигуры всегда являются двумерными. Это означает, что они имеют только длину и ширину, не имея третьей координаты в пространстве.
Во-вторых, такие фигуры могут быть различных форм и размеров. Они могут быть как простыми, например, окружностями и эллипсами, так и сложными, например, многоугольниками и кривыми.
Также, поведение и свойства таких фигур зависят от формы и свойств самой поверхности. Например, если поверхность имеет эллиптическую форму, то пересечение с плоскостью может создать эллипс или эллиптическую дугу.
Кроме того, пересечение поверхности с плоскостью может создать как замкнутые, так и незамкнутые фигуры. Замкнутые фигуры, такие как окружности и эллипсы, имеют конечный периметр и могут быть ограничены. Незамкнутые фигуры, например, линии и кривые, не имеют конечного периметра и могут быть бесконечными.
Также важно учитывать параметры плоскости, по которой происходит пересечение. Положение плоскости относительно поверхности может влиять на форму и свойства получаемых фигур. Например, пересечение плоскостью, параллельной оси симметрии поверхности, может создать фигуру с осевой симметрией.
В целом, фигуры, получаемые при пересечении поверхности с плоскостью, очень разнообразны и могут иметь множество свойств, которые зависят от формы поверхности, формы и положения плоскости, а также их взаимного взаимодействия.
Граница фигуры
Граница фигуры может иметь различную форму и сложность в зависимости от геометрических свойств поверхности и плоскости пересечения. Она может быть прямой, кривой или состоять из нескольких сегментов.
Граница фигуры часто используется в математике и графике для описания и визуализации различных объектов. Она может быть контуром плоской фигуры, такой как круг, прямоугольник или треугольник, или контуром сложной трехмерной фигуры, такой как сфера, куб или пирамида.
Часто граница фигуры имеет важные свойства и характеристики, такие как длина, площадь или объем. Они могут быть использованы для расчета и анализа геометрических параметров фигуры, а также в решении различных задач и проблем.
Таким образом, граница фигуры является важным понятием в геометрии и математике, помогающим понять и изучить формы и структуры различных объектов.
Вопрос-ответ:
Как называется фигура полученная при пересечении поверхности с плоскостью?
Фигура, полученная при пересечении поверхности с плоскостью, называется сечением.
Что происходит, когда плоскость пересекает поверхность?
Когда плоскость пересекает поверхность, происходит образование сечения, то есть фигуры, образованной на пересечении этих двух объектов.
Какие бывают сечения?
Сечения бывают разных форм и размеров, в зависимости от того, какая плоскость пересекает поверхность. Например, сечениями могут быть прямоугольники, круги, эллипсы, параболы и другие геометрические фигуры.
Зависит ли форма сечения от формы поверхности?
Да, форма сечения зависит от формы поверхности. Например, если поверхность имеет форму цилиндра, то сечение будет круглым, а если поверхность имеет форму куба, то сечение будет прямоугольником.
Зачем изучать сечения поверхностей?
Изучение сечений поверхностей помогает понять геометрические свойства объектов и применять их в решении различных математических и инженерных задач. Также изучение сечений полезно для создания моделей и дизайна, а также в проектировании и архитектуре.