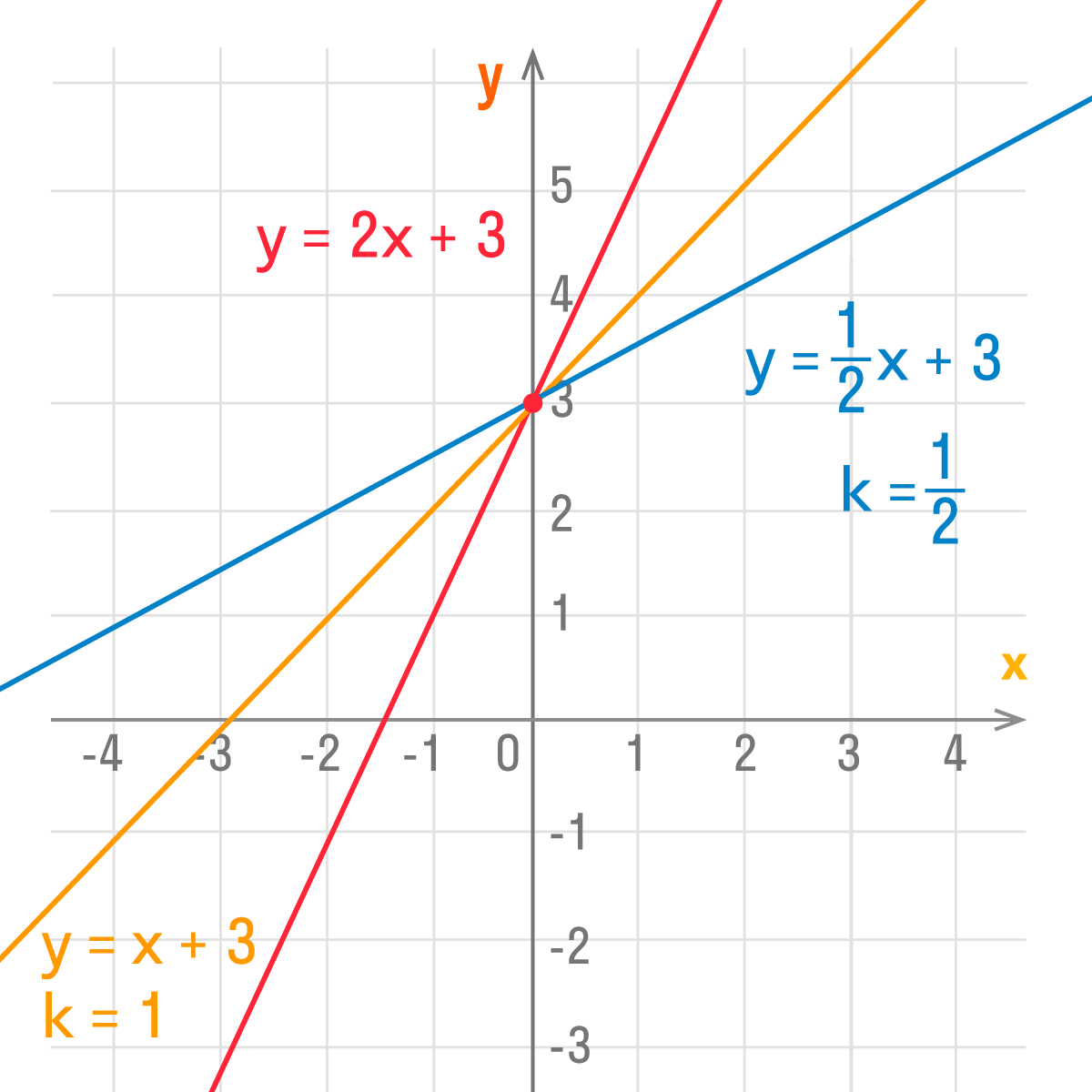
График функции – это графическое представление зависимости одной переменной от другой. Он демонстрирует изменение значения функции в зависимости от входного значения. График функции может быть полезен при анализе и визуализации математических и научных данных, а также при решении различных задач.
Построение графика функции – это процесс создания графического представления функции на координатной плоскости. Для этого необходимо знать саму функцию и ее область определения.
Сначала нужно определить множество значений, которые может принимать независимая переменная, то есть построить оси координат – горизонтальную ось абсцисс (x) и вертикальную ось ординат (y). Затем следует выбрать набор точек на графике, рассчитав значения зависимой переменной для различных значений независимой переменной.
Определение графика функции
График функции обычно представляется на плоскости, где ось абсцисс отражает значения входного параметра (обычно обозначается как x), а ось ординат — значения выходного параметра (обычно обозначается как y). Каждой точке на графике соответствует пара значений (x, y), где x — входной параметр, а y — соответствующее значение функции.
Простейший способ построения графика функции — это задание некоторого количества значений входного параметра и вычисление соответствующих значений функции для каждого значения. Затем эти точки отмечаются на координатной плоскости и соединяются линиями или кривыми.
Пример:
Рассмотрим функцию y = x^2. Мы можем выбрать несколько значений для x, например, -2, -1, 0, 1 и 2, и вычислить соответствующие значения функции:
Для x = -2, y = (-2)^2 = 4
Для x = -1, y = (-1)^2 = 1
Для x = 0, y = 0^2 = 0
Для x = 1, y = 1^2 = 1
Для x = 2, y = 2^2 = 4
Теперь мы можем отметить эти точки на графике и соединить их линиями. Полученный график будет представлять функцию y = x^2.
Понятие графика функции
Для построения графика функции необходимо:
1. Определить область значений аргумента, то есть интервал, в котором будут изменяться значения аргумента. Этот интервал может быть задан числами, символами или выражениями.
2. Найти значение функции для каждого значения аргумента в заданном интервале. Для этого необходимо подставить значения аргумента в выражение функции и вычислить соответствующие значения функции.
3. Построить систему координат на плоскости и отметить на ней найденные значения. Для этого можно использовать горизонтальную ось — ось абсцисс (x) для отображения аргумента и вертикальную ось — ось ординат (y) для отображения значения функции.
4. Соединить отмеченные точки прямыми линиями или гладкой кривой. Полученная кривая называется графиком функции.
График функции является важным инструментом для визуализации и анализа поведения функций. Он позволяет определить основные характеристики функции, такие как экстремумы, асимптоты, интервалы монотонности, пересечения с другими графиками функций и многое другое.
Функциональная зависимость и ее визуализация
Визуализация функциональной зависимости осуществляется с помощью графика функции. График представляет собой геометрическое изображение функции на координатной плоскости. При построении графика функции используются вычисления значений функции для различных входных данных и соответствующая отметка на плоскости.
Основные шаги построения графика функции:
- Выбор системы координат. Наиболее распространенная система координат — декартова система с осями x и y.
- Определение диапазона значений для осей. Этот шаг включает выбор диапазона значений для переменных x и y в функции.
- Вычисление значений функции. Путем подстановки различных значений переменной x в функцию вычисляются соответствующие значения переменной y.
- Построение точек на плоскости. Координаты точек (x, y) отображаются на плоскости, чтобы получить график функции.
- Соединение точек. С помощью линий или кривых соединяются точки на графике, чтобы получить непрерывную функцию.
Визуализация функциональной зависимости позволяет наглядно представить изменение выходных значений функции в зависимости от входных данных. График функции может помочь в анализе функций, поиске экстремумов, интерпретации данных и принятии решений в различных областях, таких как наука, экономика и техника.
Изучение функциональной зависимости и ее визуализация являются важными инструментами в анализе и понимании различных явлений и процессов. Построение графика функции позволяет увидеть общую картину изменения функции и выявить закономерности.
Значение графика функции для анализа данных
Значение графика функции для анализа данных состоит в том, что он позволяет определить основные характеристики функции, такие как максимальное и минимальное значение, точки экстремума, значения функции на определенных интервалах и так далее. График функции также помогает понять, какие значения функции соответствуют определенным входным значениям и насколько эта зависимость является линейной или нелинейной.
С помощью графика функции можно определить пересечение функции с осью абсцисс и ординат, что может быть полезно для решения уравнений и систем уравнений. Также график функции позволяет определить изменение функции во времени или в зависимости от других факторов.
График функции может быть использован для сравнения различных функций, а также для анализа и предсказания поведения функции в будущем. Поэтому строительство графика функции является важным этапом при работе с данными и может помочь в принятии важных решений на основе полученной информации.
Построение графика функции
График функции отображает зависимость значений функции от её аргумента на координатной плоскости. Построение графика позволяет визуально представить изменения функции и выявить её основные свойства.
Для построения графика функции необходимо создать таблицу, в которой указываются значения аргумента и соответствующие значения функции. Затем эти точки отмечаются на координатной плоскости и соединяются линиями.
Для начала выбирается диапазон значений аргумента, в котором будет строиться график. Затем в этом диапазоне выбираются несколько значений аргумента, для которых вычисляются соответствующие значения функции. Полученные значения заносятся в таблицу.
После того, как значения аргумента и функции занесены в таблицу, можно приступать к построению графика. Используя координатную плоскость, значения аргумента откладываются на горизонтальной оси (оси абсцисс), а значения функции на вертикальной оси (оси ординат). Для каждой точки из таблицы на плоскости отмечается отметка. Затем отметки соединяются линией. Полученная линия и будет являться графиком функции.
Построение графика функции позволяет более наглядно представить, как меняется значение функции в зависимости от её аргумента и выделить основные свойства функции, такие как возрастание, убывание, экстремумы и разрывы.
Выбор функции
Перед началом построения графика функции необходимо выбрать саму функцию, которую мы будем изучать.
Функция является математическим объектом, который связывает каждому элементу одного множества (называемого областью определения функции) элемент другого множества (называемого областью значений функции). Выбор функции зависит от конкретных задач и исследований, которые необходимо провести.
Некоторые из самых распространенных функций, которые можно выбрать для построения графиков, включают:
| Функция | Описание |
| Линейная функция | Функция, задаваемая уравнением вида y = kx + b, где k и b — константы. |
| Квадратичная функция | Функция, задаваемая уравнением вида y = ax^2 + bx + c, где a, b, и c — константы. |
| Экспоненциальная функция | Функция, задаваемая уравнением вида y = a^x, где a — константа. |
| Логарифмическая функция | Функция, задаваемая уравнением вида y = loga(x), где a — константа. |
| Тригонометрическая функция | Функция, связывающая угол с отношением длин сторон в прямоугольном треугольнике. |
Это лишь небольшой список функций, и выбор функции, конечно, зависит от твоих потребностей и вопросов, которые ты хочешь исследовать.
Каждая функция имеет свои особенности и применения, и знание этих функций поможет тебе правильно построить график и анализировать результаты.
Определение области определения и области значений
График функции представляет собой графическое изображение функции, которое позволяет наглядно представить ее поведение и свойства на протяжении всего множества значений аргумента. Однако, перед тем как приступить к построению графика, необходимо определить область определения и область значений функции.
Область определения (ОД) функции – множество значений аргумента, для которых функция имеет смысл и определена. Другими словами, это все значения, которые можно подставить в функцию и получить для них определенные значения функции.
Область значений (ОЗ) функции – множество значений, которые принимает функция при изменении значения аргумента в своей области определения. Иными словами, это все значения, которые может принимать функция.
ОД и ОЗ могут быть представлены числами, интервалами или сочетаниями этих двух форм представления. Например, для функции f(x) = √(x), область определения – положительные числа (ОД = [0, +∞)), а область значений – также положительные числа (ОЗ = [0, +∞)).
Определение области определения и области значений функции является необходимым шагом перед построением графика, так как позволяет определить, какие значения нужно учитывать при отображении функции и какие значения она может принимать.
Построение осей и единиц измерения
Построение графика функции начинается с построения осей координат. Горизонтальная ось называется осью X, а вертикальная ось называется осью Y. Отметки на осях образуют единицы измерения, которые помогают нам определить расстояние на графике.
Каждая ось имеет свою начальную точку, которая называется началом координат. Обычно начало координат обозначается буквой O. Ось X располагается в горизонтальном направлении, а ось Y — в вертикальном направлении.
Отметки на осях образуют единицы измерения. Часто для удобства используются одинаковые единицы измерения по обеим осям, однако это не всегда так. Например, при построении графика функции, осям могут соответствовать разные единицы измерения: по оси X — время, а по оси Y — расстояние.
Единицы измерения на осях позволяют наглядно представить соотношение значений функции. Кроме того, они помогают в определении точек на графике и визуально оценить изменения функции.
Оси и единицы измерения играют важную роль в построении графика функции и помогают нам лучше понять и визуализировать математические зависимости.
Вопрос-ответ:
Что такое график функции?
График функции — это визуальное представление зависимости между входными и выходными значениями функции. Он показывает, какие значения принимает функция на различных точках своего области определения.
Зачем нужно строить график функции?
Построение графика функции помогает визуализировать ее поведение и понять ее основные свойства, такие как возрастание, убывание, экстремумы и точки перегиба. График функции также может помочь найти решения уравнений и неравенств, а также предсказать значения функции в определенных точках.
Как построить график функции?
Для построения графика функции нужно сначала определить область определения функции. Затем можно выбрать набор значений аргумента в этой области и вычислить соответствующие значения функции. Пары значений аргумента и функции могут быть представлены в виде точек на координатной плоскости, которые затем соединяются линиями или кривыми. Полученный график отображает зависимость функции от аргумента.
Как выбирать значения аргумента для построения графика функции?
Выбор значений аргумента зависит от области определения функции и целей построения графика. В общем случае, полезно выбирать значения аргумента равномерно на всей области определения или при фиксированных интервалах. Однако, в некоторых случаях может быть полезно выбрать значения аргумента таким образом, чтобы подчеркнуть особенности функции, такие как точки перегиба или экстремумы.
Какие свойства графика функции можно узнать из его вида?
График функции может дать информацию о ее основных свойствах, таких как возрастание и убывание, экстремумы, точки перегиба и симметрии. Например, если график функции возрастает на определенном интервале, то это означает что функция также возрастает на этом интервале. Аналогично, если график функции имеет точку перегиба, это может означать изменение выпуклости или вогнутости функции.
Что такое график функции?
График функции — это графическое представление зависимости значения функции от ее аргумента. Он показывает, как значения функции меняются при изменении аргумента. График функции представляет собой набор точек на плоскости, где аргумент откладывается по горизонтальной оси, а значение функции — по вертикальной оси.
Как построить график функции?
Для построения графика функции необходимо выполнить несколько шагов. Во-первых, определить область определения функции, то есть множество всех значений аргумента, для которых функция определена. Затем, можно построить таблицу значений функции, выбрав некоторые значения аргумента и рассчитав соответствующие значения функции. Далее, на координатной плоскости нужно отметить найденные точки и провести сквозь них плавную кривую, отражающую характер изменения функции. Важно учесть особенности функции, такие как асимптоты, точки перегиба и т.д. В конечном итоге, получится график, который позволяет визуально представить поведение функции и анализировать ее свойства.