
Окружность — это геометрическая фигура, состоящая из всех точек в плоскости, которые находятся на одинаковом расстоянии от какой-то фиксированной точки, называемой центром окружности. Одним из наиболее важных понятий, связанных с окружностью, является диаметр.
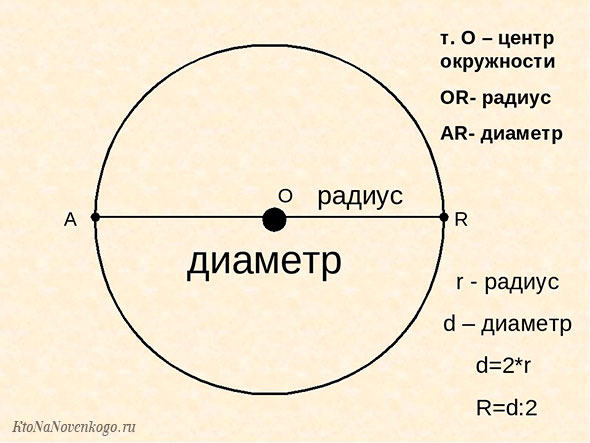
Диаметр окружности — это отрезок, который соединяет две точки окружности и проходит через ее центр. Он является самым длинным отрезком в окружности и делит ее на две половины, называемые полуокружностями.
Длина диаметра в два раза больше, чем радиус окружности. Другими словами, если радиус равен R, то длина диаметра будет равна 2R. Диаметр является одним из основных параметров окружности, вместе с радиусом и длиной окружности.
Использование диаметра в геометрии очень распространено. Он используется для определения центра и других характеристик окружности, а также для решения различных задач и построения геометрических фигур. Знание понятия диаметра окружности позволяет лучше понимать и анализировать окружности и их свойства в различных областях знаний.
Значение диаметра окружности
Диаметр окружности играет важную роль в геометрии и тесно связан с другими характеристиками окружности. Например, диаметр определяет длину окружности — расстояние, которое нужно пройти по окружности, чтобы вернуться в исходную точку.
Также диаметр используется при вычислении площади круга — фигуры, ограниченной окружностью. Площадь круга равна произведению квадрата радиуса на число π (пи).
В общем случае, диаметр окружности можно определить, зная координаты двух ее точек или с помощью специальных инструментов, таких как штангенциркуль или линейка.
Значение диаметра окружности является одним из ключевых понятий геометрии, которое находит применение не только в математике, но и в различных областях науки и техники.
Определение диаметра окружности
Длина диаметра равна удвоенной длине радиуса окружности. Диаметр также является осью симметрии для окружности, и любая прямая, перпендикулярная диаметру и проходящая через его концы, будет проходить через центр окружности.
На практике, чтобы найти диаметр окружности, достаточно измерить расстояние между двумя точками на окружности, проходящими через ее центр.
Вычисление диаметра окружности
Вычисление диаметра окружности может быть осуществлено по формуле:
| Значение | Формула |
|---|---|
| Диаметр (D) | D = 2 * R |
где D — диаметр окружности, R — радиус окружности.
Таким образом, для вычисления диаметра окружности необходимо умножить радиус на 2. Эта операция позволяет нам определить длину самого длинного отрезка, проходящего через центр окружности.
Использование диаметра окружности
Использование диаметра окружности может быть разнообразным:
| 1. Расчет длины окружности | Для вычисления длины окружности можно воспользоваться формулой: Длина окружности = пи * диаметр. Используя диаметр, можно быстро и точно определить длину окружности. |
| 2. Вычисление площади круга | Площадь круга можно найти, зная лишь диаметр. Формула для вычисления площади круга выглядит следующим образом: Площадь круга = пи * (диаметр / 2)^2. Диаметр, наряду с пи, является основой для определения площади круга. |
| 3. Определение радиуса окружности | Радиус окружности можно выразить через диаметр, применив следующую формулу: Радиус = диаметр / 2. Зная диаметр, можно легко найти соответствующий радиус, который также является важной характеристикой окружности. |
Таким образом, использование диаметра окружности позволяет решать различные задачи в геометрии, связанные с вычислениями длины окружности, площади круга и определением радиуса. Знание и применение диаметра помогает в изучении и практическом использовании окружностей и кругов в различных сферах науки и техники.
Связь диаметра с другими параметрами окружности
Длина диаметра (D) окружности связана с ее длиной (L) и радиусом (r) следующим образом:
1. Связь с длиной окружности

Длина окружности (L) равна произведению диаметра на число π (3.14159…) или двум радиусам и числу π. Формула связи между длиной окружности и диаметром имеет вид:
L = D × π
2. Связь с радиусом окружности
Радиус окружности (r) равен половине ее диаметра. Таким образом, связь между радиусом и диаметром может быть выражена следующей формулой:
r = D / 2
Знание диаметра окружности позволяет определить и другие параметры, такие как площадь и периметр окружности.
Размеры и измерение диаметра
Диаметр обычно обозначается буквой D или d. Величину диаметра можно измерить в единицах длины, таких как метры, сантиметры или миллиметры. Например, если диаметр окружности равен 10 сантиметрам, то это значит, что расстояние между двумя противоположными точками на окружности составляет 10 сантиметров.
В привычном повседневном определении диаметра всегда подразумевается прямой диаметр. Это значит, что отрезок, соединяющий две противоположные точки на окружности, является прямым отрезком.
Диаметр окружности — это характеристика, которая часто используется при решении геометрических задач. Измеряя диаметр, мы можем определить другие важные параметры окружности, такие как ее радиус, длина окружности, площадь и др. Поэтому изучение диаметра является важным элементом в школьном курсе геометрии.
Единицы измерения диаметра
Единицы измерения диаметра могут быть различными и зависят от конкретной сферы, в которой применяются. Рассмотрим некоторые из них:
- Миллиметр (мм): наиболее распространенная единица измерения малых размеров. Часто используется в инженерном делении и изготовлении мелких деталей.
- Сантиметр (см): широко применяется в быту и строительстве для измерения размеров и расстояний.
- Метр (м): основная единица длины в Международной системе единиц (СИ) и используется во многих областях, таких как строительство, наука и спорт.
- Километр (км): единица измерения больших расстояний, например, при измерении длины дорог и трасс.
Выбор единицы измерения зависит от конкретной задачи и требований точности. При работе с малыми размерами удобнее использовать миллиметры или сантиметры, а при измерении больших расстояний предпочтительнее использовать метры или километры.
Точность измерения диаметра
Окружность может иметь различные диаметры, и точность измерения диаметра играет решающую роль в получении верных результатов. Для достижения высокой точности измерения диаметра, необходимо следовать определенным правилам и использовать специальные инструменты.
Один из наиболее распространенных методов измерения диаметра — использование микрометра или калипера. Микрометр является точным инструментом, позволяющим измерять диаметр с высокой степенью точности. При использовании микрометра необходимо убедиться, что инструмент правильно прижимается к окружности и затягивается достаточно, чтобы предотвратить любые непредвиденные колебания или погрешности.
Также следует помнить, что окружность может быть не идеально округлой, и ее форма может немного меняться в зависимости от различных факторов, таких как температура или давление. Поэтому при измерении диаметра рекомендуется проводить несколько измерений в разных точках окружности и находить среднее значение, чтобы снизить погрешность.
При использовании механических инструментов для измерения диаметра также важно учитывать их погрешность. Каждый инструмент имеет свою погрешность, которую нужно учесть при получении результатов. Для увеличения точности измерения рекомендуется использовать более точные инструменты или методы измерения, например, оптические системы или лазерные дальномеры.
Итак, точное измерение диаметра окружности является важной задачей, требующей использования правильных инструментов и методов. Следуя рекомендациям и правилам точного измерения, можно получить достоверные результаты и избежать возможных погрешностей.
Вопрос-ответ:
Что такое диаметр окружности?
Диаметр окружности — это отрезок, соединяющий две точки на окружности и проходящий через ее центр.
Как найти диаметр окружности?
Диаметр окружности можно найти, зная радиус окружности и умножив его на 2. То есть диаметр равен двум радиусам.
Чем отличается диаметр от радиуса окружности?
Диаметр окружности — это отрезок, соединяющий две точки на окружности и проходящий через ее центр. Радиус окружности — это отрезок, соединяющий центр окружности с любой точкой на ней. Диаметр равен двум радиусам.
Зачем нужен диаметр окружности?
Диаметр окружности является одной из основных характеристик окружности. Он используется для вычисления других параметров окружности, таких как площадь и длина окружности.
Какой символ используется для обозначения диаметра окружности?
Обычно для обозначения диаметра окружности используется символ «d».
Что такое диаметр окружности?
Диаметр окружности — это отрезок, соединяющий две точки на окружности и проходящий через ее центр. Другими словами, диаметр — это самая длинная хорда окружности.