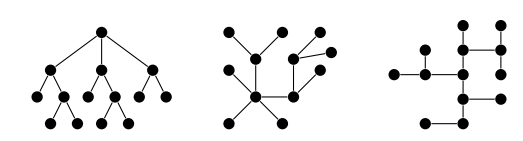
Дерево — одна из основных структур данных в теории графов. В теории графов граф представляет собой абстрактную модель, представленную набором вершин и ребер, которые их соединяют. Дерево — это связный граф, который не содержит циклов. Каждое дерево состоит из вершин и ребер, где каждая вершина имеет свой номер, информацию или значение, а каждое ребро представляет собой связь между двумя вершинами.
Деревья являются важной структурой данных в информатике и компьютерных науках, и они имеют множество применений и особенностей. Одной из ключевых особенностей дерева является его уникальная структура и отсутствие циклов, что делает его идеальным для моделирования иерархических отношений и организации данных.
Деревья также обладают несколькими важными свойствами, которые делают их полезными в различных алгоритмах и приложениях. Например, каждое дерево имеет одну вершину, называемую корневой, которая служит исходной точкой для обхода дерева. Кроме того, каждая вершина дерева может иметь некоторое количество дочерних вершин, которые связаны с ней ребрами. Дерево также может быть двоичным, когда каждая вершина имеет не более двух дочерних вершин.
Деревья широко используются в различных областях, включая базы данных, компьютерную графику, алгоритмы поиска и многие другие. Благодаря своей структуре и свойствам, деревья обеспечивают эффективное хранение и обработку данных, а также позволяют эффективно решать различные задачи. Поэтому понимание деревьев и их особенностей является важным аспектом в изучении теории графов и информатики в целом.
Определение дерева в теории графов
В дереве нет повторяющихся ребер или кратных ребер, и каждая вершина, кроме одной, имеет ровно одно ребро, ведущее в нее. Отсутствие циклов в дереве обеспечивает его характеристику связности, а свойство единственного пути между любыми двумя вершинами позволяет использовать дерево для решения различных задач, таких как поиск, сортировка и оптимизация.
Деревья широко применяются в различных областях, включая компьютерные науки, математику, биологию и сетевую теорию. Они являются фундаментальной структурой данных и инструментом для организации и хранения информации. Важно отметить, что деревья представляют собой упорядоченные структуры, где каждая вершина имеет определенное положение относительно других вершин.
Определение дерева
Особенностью дерева является наличие вершины, которая не имеет входящих ребер и называется корневой вершиной. Каждая вершина дерева, кроме корня, имеет ровно одну входящую вершину и ноль или более исходящих вершин. Вершины дерева могут быть упорядочены в иерархическую структуру, где каждая вершина ниже корня является потомком корня и имеет одного родителя.
Дерево широко применяется в различных областях, включая информатику, биологию, математику и другие науки. Оно позволяет представить иерархические отношения между объектами и решать широкий спектр задач, таких как поиск, сортировка, маршрутизация и многое другое.
Связь между вершинами
В дереве, каждая вершина имеет связь только с одной родительской вершиной, за исключением корневой вершины, которая не имеет родительской вершины. Такая структура обеспечивает уникальность иерархии в дереве.
Каждая вершина также может иметь несколько дочерних вершин, но эти дочерние вершины не могут иметь связи между собой. Таким образом, дочерние вершины представляют собой «листья» дерева, не имеющие связи с другими вершинами, кроме своего родительского элемента.
Эта связь между вершинами в дереве обуславливает множество применений и особенностей в теории графов, таких как простота поиска пути от одной вершины к другой, упорядоченность и иерархичность структуры, и многое другое.
| Вершина A | Вершина B |
|---|---|
| Родительская вершина | Дочерняя вершина |
| Родительская вершина | Дочерняя вершина |
| Родительская вершина | Дочерняя вершина |
Особенности дерева
1. Связность: Дерево состоит из связанных узлов, где каждый узел имеет ровно одного предка, кроме корневого узла, у которого нет предка. Все узлы дерева таким образом связаны друг с другом.
2. Отсутствие циклов: Дерево не содержит циклов, то есть не существует пути, который начинается и заканчивается в одном и том же узле. Это гарантирует единственность пути между любыми двумя узлами.
3. Уникальность пути: Между любыми двумя узлами существует только один путь в дереве. Это позволяет эффективно находить и перемещаться между узлами.
4. Отсутствие ориентации: В дереве отсутствует направление, то есть ребра не имеют стрелок или указателей на направление. Это делает дерево более гибким и универсальным для различных задач и алгоритмов.
5. Минимальное количество ребер: Дерево имеет минимальное возможное количество ребер для заданного числа узлов. В частности, дерево с n узлами имеет ровно n-1 ребро.
6. Иерархическая структура: Дерево образует иерархическую структуру, где каждый узел может иметь несколько потомков, но только одного предка. Это позволяет организовывать данные и моделировать различные иерархии и отношения между ними.
Все эти особенности делают дерево полезным инструментом в различных областях, таких как информатика, математика, биология, физика и т.д.
Отсутствие циклов
В дереве же такие замкнутые пути исключаются. Каждая вершина имеет только одного родителя (за исключением корневой вершины, у которой нет родителя), и поэтому невозможно вернуться к уже посещенным вершинам.
Отсутствие циклов делает дерево удобной структурой данных в различных областях: от алгоритмов поиска и сортировки до организации файловой системы. В дереве можно эффективно хранить и организовывать информацию, а также осуществлять поиск и обход вершин.
Ключевой момент: отсутствие циклов гарантирует, что в дереве существует только один путь от корневой вершины к каждой другой вершине. Это свойство делает дерево полезным и эффективным инструментом для решения разнообразных задач.
Связность и корневая вершина
Корневая вершина также является важной особенностью дерева. Визуально корневая вершина представляет собой вершину, от которой начинаются все пути в дереве. Данный концепт позволяет использовать дерево в качестве иерархической структуры, где каждая вершина имеет своего родителя и потомков.
| Пример дерева с корневой вершиной | |
| Вершина | Родитель |
| A | — |
| B | A |
| C | A |
| D | B |
| E | B |
В данном примере вершина A является корневой вершиной, от которой исходят все пути. Вершины B и C являются потомками вершины A, а вершины D и E являются потомками вершины B. Это иерархическое представление дерева позволяет удобно организовывать и структурировать данные.
Уникальность пути между вершинами
Дерево в теории графов имеет свойство уникальности пути между любыми двумя вершинами. Это означает, что для каждой пары вершин существует только один путь, который связывает их между собой.
Уникальность пути обеспечивает определенную структуру дерева. Каждая вершина имеет только одного родителя (кроме корня), и каждая вершина имеет от нуля до нескольких дочерних вершин. Это означает, что в дереве нет циклов, то есть путь не может проходить через одну вершину дважды.
Уникальность пути также означает, что для поиска определенного пути необходимо выполнить только одну последовательность шагов. Если требуется найти путь от вершины A к вершине B, то существует только один путь, который можно использовать для достижения этой цели.
Дерево с уникальными путями между вершинами играет важную роль в различных приложениях, таких как поиск и сортировка данных, алгоритмы маршрутизации в компьютерных сетях и многое другое. Уникальность пути обеспечивает эффективность и точность выполнения различных операций на дереве.
Вопрос-ответ:
Что такое дерево в теории графов?
Дерево в теории графов – это связный граф, который не содержит циклов. В дереве каждая пара вершин соединена единственным путем.
Как можно определить дерево в теории графов?
Дерево можно определить по нескольким признакам. Во-первых, дерево должно быть связным, то есть между любой парой вершин должен существовать путь. Во-вторых, дерево не должно содержать циклов, то есть нельзя пройти по графу и вернуться в исходную точку.
В чем особенности дерева в теории графов?
Дерево в теории графов обладает несколькими особенностями. Во-первых, оно является связным графом, то есть между любой парой вершин существует путь. Во-вторых, дерево не содержит циклов, что делает его структурой безликообразной. Кроме того, в дереве каждая вершина имеет ровно одну входящую связь, кроме корневой вершины, у которой нет входящих связей.
Какие есть примеры деревьев в теории графов?
Примерами деревьев в теории графов могут быть древовидные структуры, такие как семейное дерево, дерево каталогов на компьютере, представление иерархий в организации и многое другое. Все эти структуры обладают свойствами дерева, такими как отсутствие циклов и связность.