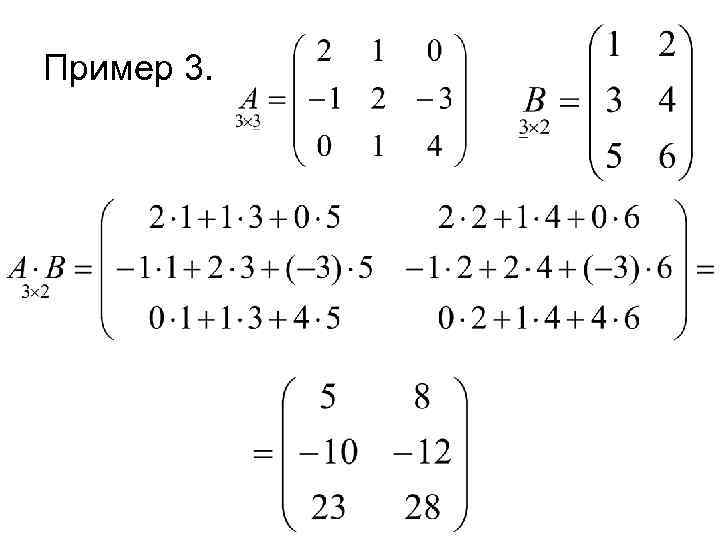
Диагональная матрица – это особый вид квадратной матрицы, у которой все элементы, находящиеся вне главной диагонали, равны нулю. Главная диагональ – это линия, проходящая от верхнего левого угла матрицы до нижнего правого угла и содержащая все элементы, которые находятся на позициях (i, i), где i – номер строки (или столбца) матрицы.
Диагональные матрицы широко применяются в различных областях математики и её приложений, таких как линейная алгебра, численные методы, физика, экономика и др. Они позволяют упростить множество вычислений и операций с матрицами благодаря своей структуре и особенностям.
Особое внимание уделяется диагональным матрицам в линейной алгебре. Их свойства и особенности исследуются при решении систем линейных уравнений, нахождении собственных значений и векторов, а также во многих других задачах. Благодаря простоте и понятности, они часто используются при демонстрации и объяснении различных математических концепций и операций.
Что такое диагональная матрица?
Каждый элемент на главной диагонали называется диагональным элементом. Остальные элементы матрицы, которые находятся вне главной диагонали, называются внедиагональными элементами. Значение внедиагональных элементов всегда равно нулю.
Диагональные матрицы широко используются в линейной алгебре и математическом моделировании. Они обладают рядом полезных свойств и применяются в различных задачах, таких как решение систем линейных уравнений, вычисление собственных значений и векторов, и других задачах, где требуется эффективная обработка данных.
Свойства диагональных матриц
Диагональной матрицей называется квадратная матрица, у которой все элементы, кроме диагональных, равны нулю. В этой статье мы рассмотрим некоторые свойства диагональных матриц.
1. Сложение и вычитание: Если имеются две диагональные матрицы одинакового порядка, то их сумма (разность) также будет диагональной матрицей. При этом элементы на главной диагонали складываются (вычитаются) поэлементно.
2. Умножение на скаляр: Если диагональную матрицу умножить на скаляр, то каждый элемент на главной диагонали будет умножен на этот скаляр, а все остальные элементы останутся равными нулю.
3. Умножение: Диагональная матрица является коммутативным мультипликативным полугруппой с нулевым элементом. При умножении двух диагональных матриц их элементы на главной диагонали перемножаются, а все остальные элементы остаются равными нулю.
4. Обратная матрица: Диагональная матрица имеет обратную матрицу, если все элементы на главной диагонали отличны от нуля. При этом обратная матрица будет также являться диагональной, с элементами, обратными к соответствующим элементам на главной диагонали.
5. След матрицы: След диагональной матрицы равен сумме элементов на главной диагонали. Таким образом, для матрицы размера n порядка след равен сумме n элементов.
Диагональные матрицы встречаются во многих областях математики и физики. Из-за своих простых свойств они являются удобными для работы и применения в различных математических операциях.
Примеры диагональных матриц
Вот несколько примеров диагональных матриц:
-
Матрица 2×2, элементы на диагонали равны 3 и 5:
[3 0] [0 5]
-
Матрица 3×3, элементы на диагонали равны -2, 4 и 1:
[-2 0 0] [0 4 0] [0 0 1]
-
Матрица 4×4, элементы на диагонали равны 10, -7, 0 и 2:
[10 0 0 0] [0 -7 0 0] [0 0 0 0] [0 0 0 2]
Диагональные матрицы имеют свои особенности и применяются в различных областях математики и физики. Они широко используются для решения систем линейных уравнений, вычисления собственных значений и векторов матрицы, а также в других приложениях.
Как задать диагональную матрицу?
Существует несколько способов задать диагональную матрицу:
- Ручной ввод элементов. Вы можете задать каждый элемент матрицы вручную, указывая его значение на главной диагонали и присваивая нулевое значение всем остальным элементам:
- Использование цикла. Если вы знаете размерность матрицы, вы можете использовать цикл для заполнения элементов:
- Использование специализированных методов. Во многих языках программирования существуют специальные функции или методы для создания диагональной матрицы. Например, в языке Python можно использовать функцию
numpy.diag():
int[][] matrix = {
{1, 0, 0},
{0, 2, 0},
{0, 0, 3}
};
int n = 3; // размерность матрицы
int[][] matrix = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i == j) {
matrix[i][j] = i + 1;
} else {
matrix[i][j] = 0;
}
}
}
import numpy as np
matrix = np.diag([1, 2, 3])
Независимо от способа задания диагональной матрицы, она может быть использована в различных областях, таких как линейная алгебра, численные методы, машинное обучение и другие.
Сложение диагональных матриц
Для выполнения сложения диагональных матриц необходимо соблюдать следующие правила:
- Матрицы должны иметь одинаковые размерности. Иначе сложение невозможно.
- Элементы, не находящиеся на главной диагонали, остаются без изменений.
Пример сложения двух диагональных матриц:
Исходные матрицы:
| 3 | 0 |
| 0 | 2 |
| 1 | 0 |
| 0 | 4 |
Сложение матриц:
| 3 + 1 = 4 | 0 + 0 = 0 |
| 0 + 0 = 0 | 2 + 4 = 6 |
Результат сложения:
| 4 | 0 |
| 0 | 6 |
Таким образом, сложение диагональных матриц выполняется путем сложения соответствующих элементов каждой матрицы и приводит к образованию новой диагональной матрицы.
Умножение диагональных матриц
Для умножения двух диагональных матриц необходимо перемножить элементы на главной диагонали и получить новую диагональную матрицу, у которой элементы на главной диагонали будут равны произведению соответствующих элементов исходных матриц.
Процесс умножения двух диагональных матриц можно проиллюстрировать с помощью таблицы:
| Диагональная матрица A | * | Диагональная матрица B | = | Диагональная матрица C | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| a11 | b11 | c11 = a11 * b11 | |||||||||
| a22 | * | b22 | c22 = a22 * b22 | ||||||||
| a33 | b33 | c33 = a33 * b33 |
Таким образом, результатом умножения двух диагональных матриц A и B будет новая диагональная матрица C, у которой элементы на главной диагонали будут равны произведению соответствующих элементов исходных матриц.
Обратная диагональная матрица
Для того чтобы найти обратную диагональную матрицу, нужно взять каждый элемент на главной диагонали и заменить его на обратный. Если элемент равен нулю, то его обратного не существует, поэтому в этом случае обратной матрицы нет.
Обратная диагональная матрица обладает следующими свойствами:
- Если исходная диагональная матрица имеет некоторый элемент a на главной диагонали, то обратная диагональная матрица будет иметь элемент 1/a на том же месте.
- Если в исходной диагональной матрице на главной диагонали имеется элемент a, а на соседних диагоналях находятся элементы b и c, то в обратной диагональной матрице на главной диагонали будет находиться элемент 1/a, а на остальной части - элементы -b/a и -c/a, соответственно.
Обратная диагональная матрица используется в различных областях математики и науки, например, при решении систем линейных уравнений и вычислении определителей.
Значимость диагональных матриц в математике и науке
Значимость диагональных матриц проявляется во многих областях математики и науки:
1. Линейная алгебра

Диагональные матрицы играют ключевую роль в линейной алгебре. Они позволяют упростить многие вычисления и решения задач. Например, сложение и умножение диагональных матриц происходит очень эффективно и быстро. Кроме того, диагональность матрицы позволяет легко найти ее собственные значения и собственные векторы.
2. Теория вероятностей
В теории вероятностей диагональные матрицы используются для описания вероятностных моделей. Например, в марковских цепях, состояния системы могут быть представлены элементами диагональной матрицы. Это позволяет удобно описывать и анализировать переходы между состояниями и вероятность перехода в следующее состояние.
Диагональные матрицы также находят применение в различных областях науки, таких как физика, экономика, генетика и другие. Они упрощают формулирование и решение задач, связанных с линейными системами уравнений, преобразованиями координат, фильтрацией данных и др. Благодаря своей структуре и свойствам, диагональные матрицы являются мощным инструментом в моделировании и анализе различных процессов и явлений.
Вопрос-ответ:
Что такое диагональная матрица?
Диагональной матрицей называется квадратная матрица, у которой все элементы вне главной диагонали (т.е. элементы, расположенные не на главной диагонали) равны нулю.
Как выглядит диагональная матрица?
Диагональная матрица представляет собой квадратную таблицу, в которой значения элементов на главной диагонали отличны от нуля, а остальные элементы равны нулю.
Какие свойства имеет диагональная матрица?
Диагональная матрица обладает несколькими свойствами: все элементы вне главной диагонали равны нулю, сумма двух диагональных матриц также является диагональной матрицей, произведение двух диагональных матриц равно диагональной матрице, умноженной на произведение соответствующих элементов диагоналей и т.д.
Для чего используются диагональные матрицы?
Диагональные матрицы находят применение в различных областях, включая линейную алгебру, численные методы, физику, экономику и многие другие. Они упрощают вычисления и позволяют эффективно работать с большими объемами данных. Например, в задачах линейного программирования или в методе минимальных квадратов.