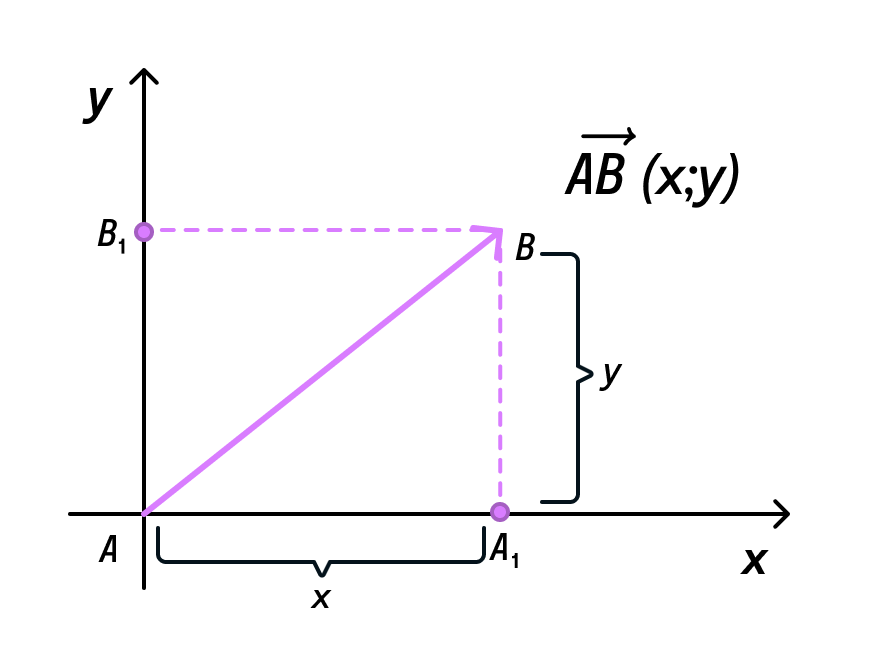
В математике вектор – это объект, характеризующийся направлением и длиной. Он представляет собой упорядоченную пару чисел или точек, где первое число определяет координату по оси X, а второе – по оси Y. Однако, длина вектора не всегда является простым числом. Понятие длины вектора позволяет оценить его «размер» и реализовать ряд математических операций.
Длина вектора вычисляется на основе его координатных значений с использованием формулы. Если вектор ненулевой, то его длина – положительное число, показывающее единицы длины (например, метры, сантиметры и т. д.). С помощью математических операций можно получить длину вектора как геометрическую величину, которая является модулем вектора.
С другой стороны, нулевой вектор имеет длину, равную нулю. Это означает, что у нулевого вектора нет направления и он не отображает никакую величину. Нулевой вектор является особенным случаем, когда его все координаты равны нулю. В то же время, он имеет значение при вычислениях и в многих математических операциях. Нулевой вектор служит часто используемым инструментом в линейной алгебре и физике.
Длина вектора и ее значение для ненулевых и нулевых векторов
Для ненулевых векторов, длина вектора рассчитывается по формуле:
||v|| = sqrt(x^2 + y^2)
где x и y — координаты вектора.
Длина нулевого вектора всегда равна нулю. В нулевом векторе нет направления и его длина равна нулю, так как начало и конец вектора совпадают.
Длина вектора имеет важное значение во многих областях науки и техники. Она позволяет определить, насколько сильно вектор воздействует или направлен в определенную сторону. Также, длина вектора используется при решении многих задач в физике, геометрии, компьютерной графике и других областях.
Что такое длина вектора?
Длина вектора обозначается символом ||v||, где v — сам вектор. Также длину вектора можно назвать его модулем или абсолютным значением.
Для вычисления длины вектора необходимо воспользоваться так называемой евклидовой нормой, которая определяется по формуле:
||v|| = sqrt(x^2 + y^2 + z^2),
где x, y и z — координаты вектора.
Ненулевой вектор имеет длину, которая больше нуля, и показывает его направление и масштаб. Вектор является нулевым, если его длина равна нулю. Нулевой вектор не содержит информации о направлении и масштабе.
Длина нулевого вектора равна нулю: ||0|| = 0.
Знание длины вектора позволяет решать множество задач, связанных с движением, силами и другими физическими явлениями.
Определение длины вектора
Длина вектора часто обозначается символом ||v|| или |v|. Она всегда неотрицательна и может быть выражена с помощью формулы:
||v|| = sqrt(v₁² + v₂² + … + vn²)
где v₁, v₂, …, vn — компоненты вектора в соответствующих направлениях.
Вектор нулевой длины называется нулевым вектором. Его длина равна нулю и он не имеет определенного направления. Ненулевой вектор имеет длину, отличную от нуля, и определенное направление в пространстве.
Длина вектора важна во множестве математических и физических приложений. Она используется, например, для измерения расстояний, определения скорости и усилий в системах сил.
Геометрическая интерпретация длины вектора
Геометрическая интерпретация длины вектора заключается в том, что длина вектора представляет собой расстояние между его начальной точкой и конечной точкой в пространстве. То есть, если мы зададим вектор в виде направленного отрезка, то его длина будет равна длине этого отрезка.
Длина ненулевого вектора может быть определена с помощью формулы длины вектора:
- Если вектор задан в координатах (x, y, z), то его длина вычисляется по формуле: √(x² + y² + z²).
- Если вектор задан в пространстве R^n, то его длина вычисляется по формуле: √(x₁² + x₂² + … + xₙ²).
Длина ненулевого вектора всегда положительна, так как это реальное расстояние в пространстве. Она может быть представлена числом величины, которая характеризует вектор.
Длина нулевого вектора также может быть определена и равна нулю. Нулевой вектор представляет собой точку, в которой нет никакого пространственного перемещения.
Именно геометрическая интерпретация длины вектора позволяет нам понять его физическую природу и применять его в решении различных задач в геометрии и физике.
Длина ненулевого вектора
Для вычисления длины вектора v в n-мерном пространстве, мы можем использовать теорему Пифагора:
Длина вектора v = √(v₁² + v₂² + … + vₙ²)
где v₁, v₂, …, vₙ — компоненты вектора v в каждом измерении.
Длина ненулевого вектора представляет собой меру его «размаха» или «магнитуды». Она показывает, насколько вектор «растянут» в каждом измерении. Чем больше длина вектора, тем больше его магнитуда.
Важно отметить, что длина ненулевого вектора всегда положительна. Если вектор является нулевым (все его компоненты равны нулю), то его длина равна нулю.
Знание длины ненулевого вектора позволяет нам сравнивать и классифицировать векторы, а также использовать их в различных математических и физических приложениях.
Вычисление длины ненулевого вектора
Для вычисления нормы вектора используется теорема Пифагора для треугольников. Если вектор представлен в виде (x, y) в координатной плоскости, то его норма вычисляется по формуле:
||v|| = √(x2 + y2)
То есть, длина вектора равна квадратному корню из суммы квадратов его координат.
Если вектор задан в трехмерном пространстве (x, y, z), то норма вычисляется по аналогичной формуле:
||v|| = √(x2 + y2 + z2)
Таким образом, длина ненулевого вектора равна квадратному корню из суммы квадратов его координат, взятых по модулю. Значение нормы вектора всегда положительно.
Свойства длины ненулевого вектора
У ненулевого вектора есть несколько свойств, связанных с его длиной:
1. Ненулевой вектор имеет положительную длину. Длина вектора всегда положительна, так как она представляет собой расстояние между началом и концом вектора. Даже если направление вектора изменено, его длина остается неизменной.
2. Длина ненулевого вектора равна нулю только в случае, если сам вектор равен нулю. Если вектор имеет длину равную нулю, то его компоненты также должны быть равны нулю. Ненулевой вектор не может иметь нулевую длину.
3. Длина ненулевого вектора может быть измерена с помощью теоремы Пифагора. Если вектор задан в прямоугольной системе координат, то его длину можно вычислить по формуле: длина = квадратный корень из (x^2 + y^2 + z^2), где x, y и z – компоненты вектора.
Все эти свойства помогают понять, как изменяется длина вектора при его преобразованиях и манипуляциях. Длина ненулевого вектора является важным понятием в математике, физике, компьютерной графике и других науках, где используются векторы для описания и анализа различных явлений и процессов.
Длина нулевого вектора
Действительно, для вычисления длины вектора используется формула:
|A| = √(a₁² + a₂² + … + aₙ²)
Где |A| — длина вектора A, a₁, a₂,…, aₙ — компоненты вектора, а √ — квадратный корень.
Если рассмотреть нулевой вектор, то все его компоненты равны нулю:
a₁ = 0, a₂ = 0, …, aₙ = 0
Подставим эти значения в формулу для длины вектора:
|A| = √(0² + 0² + … + 0²) = √0 = 0
Таким образом, длина нулевого вектора всегда будет равна нулю. Это свойство нулевого вектора следует из его определения и принимается в линейной алгебре.
Вопрос-ответ:
Что такое длина вектора?
Длина вектора — это величина, определяющая его размер или масштаб. Она измеряется в единицах длины и может быть положительной или нулевой.
Чему равна длина ненулевого вектора?
Длина ненулевого вектора определяется по формуле: длина вектора = sqrt(x^2 + y^2 + z^2), где x, y, z — координаты вектора в пространстве. Она всегда будет положительной и выражает расстояние от начала координат до конца вектора.
Чему равна длина нулевого вектора?
Длина нулевого вектора всегда будет равна нулю. Это происходит потому, что нулевой вектор не имеет направления и его начало и конец совпадают в точке начала координат.
Как вычислить длину вектора на плоскости?
Для вычисления длины вектора на плоскости, состоящего из двух компонент, можно использовать теорему Пифагора. Если вектор задан координатами (x, y), то его длина вычисляется по формуле: длина вектора = sqrt(x^2 + y^2).
Какую важную роль играет длина вектора в физике?
Длина вектора играет важную роль в физике, так как она определяет масштаб и направление физических величин, таких как сила, скорость или ускорение. От длины вектора зависит физическое воздействие и его характеристики.