Случайная величина является одним из ключевых понятий в области статистики. Она представляет собой нечто, что может принимать различные значения в рамках определенного эксперимента. Такие значения являются результатом некоторого случайного процесса или события. В статистике случайная величина может быть дискретной или непрерывной, хотя в обоих случаях она описывает вероятностные законы исследуемого явления.
Определение случайной величины является неотъемлемой частью построения статистической модели и проведения анализа данных. Чтобы определить случайную величину для конкретного эксперимента, необходимо задать всевозможные значения, которые она может принимать, а также вероятность появления каждого из этих значений. Таким образом, случайная величина может быть описана с помощью функции распределения, которая определяет вероятность того, что случайная величина примет определенное значение.
Раздел 1: Понятие случайной величины
Для определения случайной величины необходимо определить пространство элементарных исходов и набор событий, которые могут произойти. Именно в этих событиях исследуется случайная величина.
Случайные величины могут быть дискретными или непрерывными. Дискретная случайная величина принимает отдельные значения и может быть связана с подсчетом или количеством. Например, результат броска монеты (орел или решка) или число посетителей в магазине за определенный период времени.
Непрерывная случайная величина, напротив, может принимать определенный диапазон значений и связана с измерением. Например, рост человека или время, затраченное на выполнение определенной задачи.
Случайные величины могут быть также классифицированы как детерминированные или недетерминированные. Детерминированная случайная величина имеет определенную зависимость от других факторов или переменных, в то время как недетерминированная случайная величина не имеет явной зависимости.
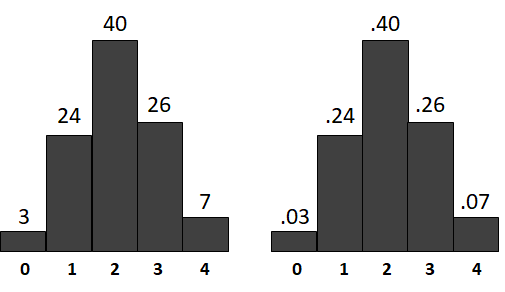
Важно отметить, что случайные величины могут быть представлены в таблице, диаграмме или графике для наглядного исследования и анализа. Это позволяет лучше понять распределение значений и вероятности их появления.
Что такое случайная величина?
Случайные величины могут быть дискретными или непрерывными в зависимости от их значения. Дискретные случайные величины могут принимать только конечное или счетное множество значений, например, число выпавших очков при броске кубика. Непрерывные случайные величины, напротив, могут принимать любое значение из некоторого интервала, например, время ожидания в очереди.
Случайные величины часто используются в статистике для изучения различных явлений и процессов. Они позволяют описывать вероятностные распределения и рассчитывать вероятности различных событий. Кроме того, они используются для оценки параметров выборки и проведения статистических тестов.
Пример 1: Пусть случайная величина X представляет собой количество успешных звонков, выполненных оператором поддержки за час работы. X может принимать значения от 0 до бесконечности, так как оператор может совершить любое количество звонков. Данная случайная величина будет являться непрерывной.
Пример 2: Пусть случайная величина Y представляет собой количество детей в семье. Y может принимать значения 0, 1, 2, 3 и так далее, так как количество детей в семье является дискретной величиной.
Изучение случайных величин позволяет более точно описывать и понимать случайные процессы и явления, а также предсказывать их поведение на основе вероятностных моделей и статистических методов.
Какие можно выделить типы случайных величин?
Существует несколько типов случайных величин, которые можно выделить в статистике:
- Дискретные случайные величины: это величины, которые могут принимать только конкретные значения из некоторого множества. Например, число выпавших орлов при подбрасывании монеты или количество посетителей в магазине за определенный промежуток времени.
- Непрерывные случайные величины: это величины, которые могут принимать любое значение из некоторого интервала или диапазона. Например, рост человека или время, затраченное на выполнение задания.
- Бинарные случайные величины: это дискретные величины, которые могут принимать только два значения — 0 и 1. Например, результат эксперимента — успех или неудача.
- Пуассоновские случайные величины: это дискретные величины, которые моделируют количество событий, происходящих в заданный промежуток времени или в заданной области. Например, количество приходящих писем в почтовый ящик за определенный период времени.
Выделение типов случайных величин позволяет проводить более точные статистические анализы и предсказания на основе собранных данных. Каждый тип имеет свои особенности и специфические методы анализа, которые нужно учитывать при работе с ними. Это позволяет более полно и точно описать случайные явления и принимать на их основе важные решения.
Что означает дискретность или непрерывность случайной величины?
Случайная величина в статистике может быть либо дискретной, либо непрерывной. Дискретная случайная величина принимает только отдельные значения в заданных пределах. Ее значения обычно состоят из отдельных точек или наборов точек на числовой оси. Примерами дискретных случайных величин могут быть количество выпавших орлов при подбрасывании монеты или количество побед в серии игр.
С другой стороны, непрерывная случайная величина может принимать любое значение в заданном диапазоне. Ее значения формируют непрерывные интервалы на числовой оси. Примерами непрерывных случайных величин могут быть рост человека, время, потраченное на выполнение задания, или скорость движения автомобиля.
Различие между дискретной и непрерывной случайной величиной заключается в том, как они представляются и обрабатываются в статистике. Для дискретной случайной величины вероятности определенных значений могут быть вычислены точно, так как она принимает только конкретные значения. В то же время, для непрерывной случайной величины мы говорим о вероятности попадания значения в определенный диапазон, так как она может принимать бесконечно много значений.
Раздел 2: Определение случайной величины
Более формально, случайная величина – это функция, которая каждому элементарному исходу эксперимента сопоставляет числовое значение. Например, при подбрасывании монеты можно определить случайную величину «X», которая принимает значение 1 в случае выпадения орла и значение 0 в случае выпадения решки.
Случайная величина может быть дискретной или непрерывной. Дискретная случайная величина принимает конечное или счетное множество значений, например, количество выпавших шестерок при бросании игральной кости. Непрерывная случайная величина, в свою очередь, принимает значения из непрерывного диапазона, например, время, потраченное на прохождение теста.
Изучение случайных величин является важным шагом на пути к пониманию и анализу статистических данных. С помощью случайных величин статистики могут описывать и анализировать разнообразные явления и процессы, такие как вероятность возникновения определенного события или оценка параметров популяции.
Как определить случайную величину в эксперименте?
Случайная величина в эксперименте определяется как функция, которая сопоставляет каждому элементу
выборки некоторое число или объект. Главная особенность случайной величины состоит в том, что она принимает
значения неоднократно, а каждое значение имеет свою вероятность.
Для определения случайной величины в эксперименте необходимо в первую очередь определить все возможные
исходы данного эксперимента и их вероятности. Исходы могут быть как числами, так и объектами. Затем, на основе
этих данных, можно составить таблицу, в которой указываются все возможные значения случайной величины и их
вероятности. После этого определение случайной величины в эксперименте может быть закончено.
Для более точного определения случайной величины в эксперименте можно использовать математические методы.
Например, в случае дискретной случайной величины можно использовать функцию распределения, которая позволяет
определить вероятность появления каждого значения случайной величины. В случае непрерывной случайной величины
можно использовать функцию плотности распределения.
Таким образом, определение случайной величины в эксперименте является важным этапом статистического анализа,
который позволяет оценить вероятности различных исходов и принять обоснованные решения на основе этих данных.
Какие методы используются для определения случайной величины в статистике?
Определение случайной величины в статистике происходит с использованием различных методов. Рассмотрим некоторые из них:
1. Экспериментальный метод:
Данный метод заключается в проведении ряда экспериментов, при которых регистрируются значения величины. Например, при исследовании случайной величины «время ожидания в очереди» проводятся наблюдения, записываются результаты для каждого эксперимента и на их основе строят эмпирическую функцию распределения или гистограмму.
2. Наблюдательный метод:
3. Теоретический метод:
Для определения случайной величины также используется теоретический метод, базирующийся на определении вероятностного распределения. Исследователь определяет вероятностные характеристики случайной величины, такие как математическое ожидание, дисперсия и функция распределения. Затем на основе этих характеристик строятся математические модели, которые могут описывать случайную величину.
4. Комбинированный метод:
Комбинированный метод предполагает использование нескольких методов одновременно. Например, при исследовании случайной величины «время доставки заказа» можно собирать данные о времени доставки, проводить эксперименты для получения новых данных и анализировать предыдущие исследования.
Использование различных методов для определения случайной величины в статистике позволяет получить более полное представление о ее характеристиках и свойствах.
Вопрос-ответ:
Что такое случайная величина?
Случайная величина – это математический объект, который моделирует результат случайного эксперимента. Она может принимать различные значения, в зависимости от того, какие исходы эксперимента будут реализованы. Например, если мы бросаем игральную кость, то результатом может быть любое число от 1 до 6, и это число будет являться значениями случайной величины.
Как определить случайную величину?
Чтобы определить случайную величину, нужно определить все возможные значения, которые она может принимать, и указать вероятность реализации каждого значения. Например, если случайная величина X представляет результат броска игральной кости, то мы можем определить, что X принимает значения от 1 до 6 с равной вероятностью 1/6.
Какие бывают типы случайных величин?
Существует два основных типа случайных величин: дискретные и непрерывные.
Что такое дискретная случайная величина?
Дискретная случайная величина может принимать только определенные значения из конечного или счетного множества. Например, число полученных головок при подбрасывании монеты – дискретная случайная величина, так как она может принимать только значения 0 или 1.
Что такое непрерывная случайная величина?
Непрерывная случайная величина может принимать любое значение на определенном интервале. Например, рост человека – непрерывная случайная величина, так как он может быть любым числом в заданном интервале.