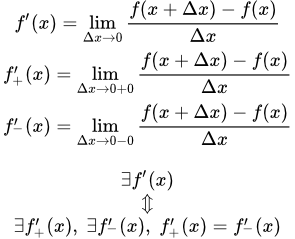
Определение производной функции в точке x0 – важное понятие в математике, которое имеет широкое применение в различных областях. Производная функции позволяет определить, как меняется значение функции при изменении аргумента. Она является основополагающим понятием в дифференциальном исчислении и играет важную роль в решении задач из физики, экономики, информатики и других наук.
Определение производной функции в точке x0 позволяет найти скорость изменения значения функции в данной точке. Если значение производной отрицательно, то функция убывает, если положительно – она возрастает. Это позволяет исследовать поведение функции и определить наличие ее экстремумов – точек минимума или максимума.
Производную функции в точке x0 можно вычислить используя пределы или же пользуясь формулами производных элементарных функций. Для этого существуют определенные правила дифференцирования, которые позволяют найти производные сложных функций, суммы, разности и произведения функций. Полученные значения производных могут быть использованы для нахождения касательной линии к графику функции, а также для решения задач оптимизации и построения функциональных моделей.
Определение производной функции в точке x0
Определение производной функции в точке x0 формализуется следующим образом:
- Пусть дана функция f(x).
- Точка x0 является внутренней точкой области определения функции f(x).
- Если существует предел отношения (f(x) — f(x0))/(x — x0) при x → x0, то этот предел называется производной функции f(x) в точке x0 и обозначается как f'(x0).
Производная функции в точке x0 показывает наклон касательной к графику функции в этой точке. Если производная положительна, то функция возрастает в данной точке, если отрицательна, то функция убывает, а если равна нулю, то функция имеет экстремум в этой точке.
Определение производной функции в точке x0 имеет широкое применение в научных и инженерных расчетах. Оно позволяет находить критические точки функций, наибольшие и наименьшие значения функций, скорость изменения величин и многое другое.
Понятие производной функции
Функция называется дифференцируемой в точке, если существует такая производная, которая представляет собой предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю. Производная функции в точке х0 обозначается f'(х0) или dy/dx|х=х0.
Производная функции показывает темп изменения значения функции в данной точке. Если производная положительна, то значение функции увеличивается, если производная отрицательна, то значение функции уменьшается. Значение производной равное нулю соответствует экстремуму функции.
Производная функции важна во многих приложениях, таких как оптимизация функций, анализ графиков функций, решение уравнений и т. д. Она также является основой для дальнейшего изучения математического анализа и вычислительной математики.
Определение производной
Производная функции f(x) в точке x₀ обозначается как f'(x₀) или df(x₀)/dx. Она определяется как предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
| Производная функции | Определение |
|---|---|
| f'(x₀) | f'(x₀) = lim(h→0) (f(x₀ + h) — f(x₀))/h |
| df(x₀)/dx | df(x₀)/dx = lim(h→0) (f(x₀ + h) — f(x₀))/h |
Определение производной позволяет найти наклон касательной к графику функции в точке x₀, а также определить производные высших порядков, что имеет важное применение в математике и её приложениях.
Геометрическая интерпретация производной
Производная функции в точке x₀ может быть геометрически интерпретирована как угловой коэффициент касательной к графику функции в этой точке.
Касательная является прямой, которая касается графика функции только в одной точке и имеет такое же направление, как и график функции в этой точке.
Угловой коэффициент касательной определяет, насколько быстро меняется значение функции при изменении аргумента. Если производная положительная, то касательная наклонена вверх, а функция возрастает. Если производная отрицательная, то касательная наклонена вниз, а функция убывает.
Таким образом, геометрическая интерпретация производной позволяет наглядно представить, как функция изменяется вблизи заданной точки, а также определить ее поведение в ней.
Физическая интерпретация производной
Производная функции в точке имеет не только математическое значение, но и физическую интерпретацию. Она позволяет понять, как изменяется величина функции при изменении её аргумента.
Например, если рассмотреть график зависимости пройденного пути от времени для движущегося объекта, то производная в определенной точке будет представлять скорость в этой точке. То есть, производная функции показывает, как быстро меняется величина функции.
Другим примером может служить зависимость силы от перемещения тела. Производная в данном случае описывает силу натяжения, которая действует на тело при его перемещении.
Применение производной функции
Одно из основных применений производной функции заключается в нахождении точек экстремума функции. Экстремумы функции представляют собой точки, где функция достигает наибольшего (максимума) или наименьшего (минимума) значения. Производная функции позволяет найти эти точки путем анализа ее поведения вблизи значений x.
Также производная функции важна для анализа скорости изменения функции в конкретной точке. График производной функции показывает наклон касательной к графику и даёт информацию о темпе изменения функции. Например, в физике производная может быть использована для определения скорости и ускорения тела.
Кроме того, производная функции помогает в построении графиков функций. Зная производную функции, можно определить, где функция возрастает, убывает, имеет точки перегиба и другие характеристики. Это позволяет более точно изучить поведение функции и выявить ее особенности.
Применение производной функции также распространено в задачах оптимизации. Например, в экономике ее используют для определения максимальной прибыли или минимальных издержек. В инженерии производная функции может помочь в оптимизации параметров системы или процесса.
Таким образом, применение производной функции позволяет более глубоко изучить свойства функций и использовать их для решения реальных задач в различных областях знания.
Нахождение экстремумов функции
Для определения экстремумов функции необходимо выполнить следующие шаги:
- Найти производную функции.
- Найти точки, где производная равна нулю или не существует.
- Проверить значения функции в найденных точках и окрестностях.
- Определить тип экстремума: максимум или минимум в соответствии с изменением знака производной.
Если значение производной равно нулю в точке x0, то функция может иметь экстремумы в этой точке. Однако необходимо учесть и другие факторы, такие как знаки производной в окрестностях точки x0. Если производная меняет знак при переходе через точку x0, то в данной точке функция достигает экстремума.
В случае, если производная не существует в точке x0, необходимо рассмотреть значение функции в окрестностях данной точки и определить, является ли она локальным максимумом или минимумом.
Нахождение экстремумов функции позволяет определить места, где функция принимает свои наибольшие и наименьшие значения. Это информация очень важна при изучении поведения функции и решении задач в различных областях науки и техники.
Вопрос-ответ:
Что такое производная функции в точке?
Производная функции в точке x0 — это предел отношения изменения значения функции к изменению аргумента при стремлении аргумента к данной точке.
Зачем нужно определять производную функции?
Определение производной функции позволяет анализировать изменение функции в различных точках, находить экстремумы функции, определять ее приближенное поведение и т.д.
Как вычислить производную функции в точке?
Для вычисления производной функции в точке x0 можно использовать различные методы, включая правило дифференцирования, правило Лопиталя, использование разложений в ряд Тейлора и т.д.
Приведите пример применения производной функции в реальной жизни.
Один из примеров применения производной функции — определение скорости изменения величин в физике. Например, скорость изменения пути по времени равна производной функции пути по времени.
Какие свойства имеет производная функции в точке?
Производная функции в точке x0 имеет свойства, такие как линейность, правило дифференцирования суммы и произведения функций, правило Лейбница и т.д.
Что такое производная функции?
Производная функции в точке x0 – это значение предела отношения приращения функции к приращению аргумента при стремлении последнего к нулю. Она показывает скорость изменения значения функции в данной точке.