Корень уравнения – это значение переменной, при котором уравнение принимает верное равенство. Найти корни уравнения является одной из важных задач алгебры и математического анализа. Определение корня уравнения дает точку пересечения графика уравнения с осью абсцисс.
Примеры уравнений со всего курса математики можно привести очень много. Вот лишь некоторые из них:
Линейное уравнение:
ax + b = 0, где a и b – известные числа, а x – неизвестная.
Квадратное уравнение:
ax^2 + bx + c = 0, где a, b и c – известные числа, а x – неизвестная.
Тригонометрическое уравнение:
sin(x) = 0, где x – угол, а sin(x) – его синус.
Логарифмическое уравнение:
log(x) = 0, где x – неизвестная, а log(x) – натуральный логарифм.
Существуют разные способы нахождения корней уравнений в зависимости от их типа. Один из самых распространенных методов – это использование формулы дискриминанта для квадратных уравнений. Для линейных и тригонометрических уравнений часто используется метод подстановки. Некоторые уравнения можно решить графически, строя график функции.
Что такое корень уравнения
Корни уравнения могут быть как действительными числами, так и комплексными числами. Действительные корни находятся на числовой прямой, в то время как комплексные корни — на комплексной плоскости.
Для нахождения корней уравнения существуют различные методы, в зависимости от типа и степени уравнения. Некоторые из них включают:
1. Метод подстановки: этот метод заключается в последовательном подставлении различных значений переменной в уравнение с целью найти такое значение, при котором уравнение равно нулю. Например, для квадратного уравнения можно подставлять различные числа и проверять, при каком значении уравнение обращается в ноль.
2. Метод факторизации: данный метод применяется для уравнений, которые могут быть разложены на множители. Заключается в разложении уравнения на произведение множителей и нахождении значений переменной, при которых каждый из множителей равен нулю.
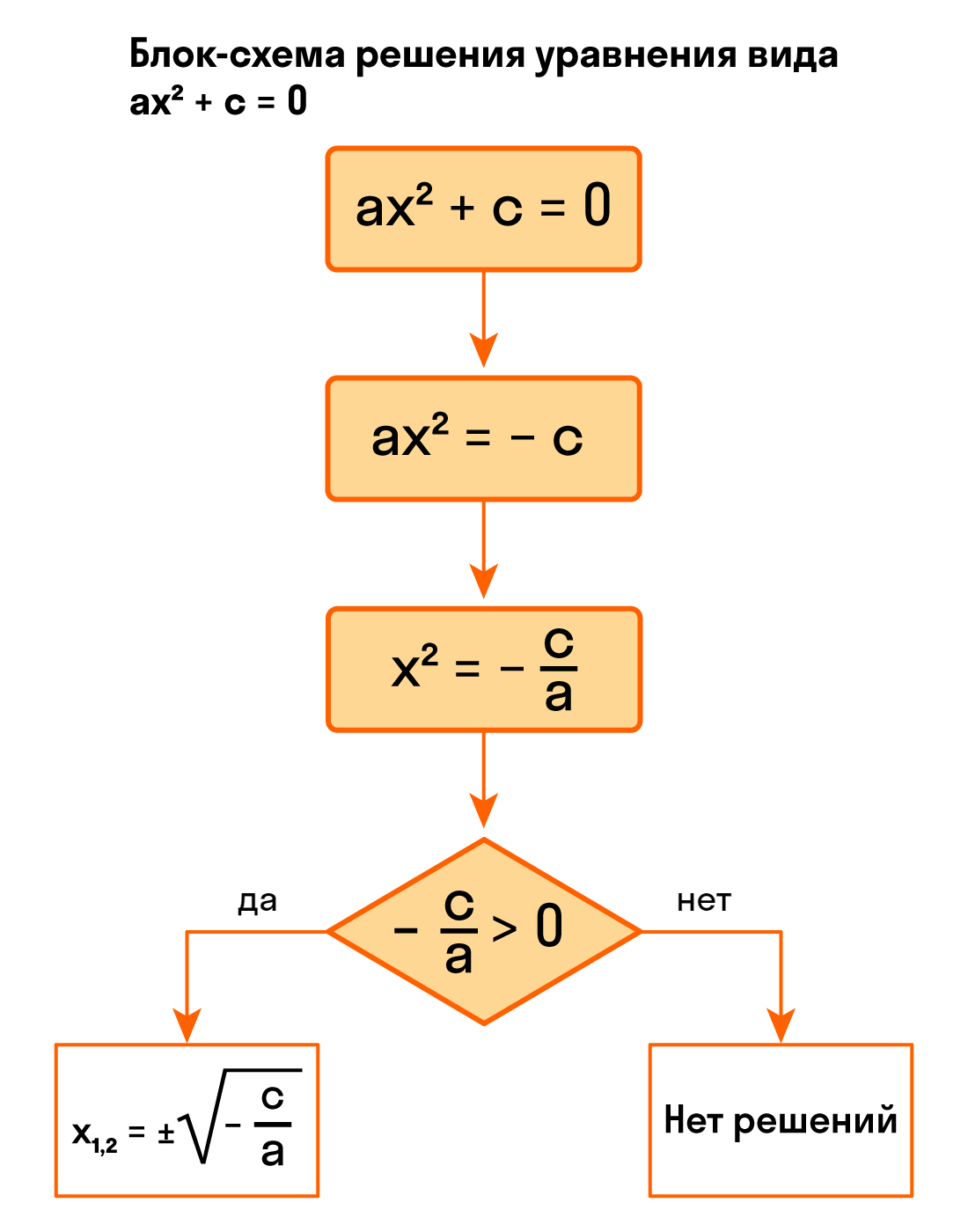
3. Метод квадратного корня: применяется для решения квадратного уравнения. Состоит в извлечении корней при помощи формулы корней квадратного уравнения.
4. Метод дискриминанта: используется для определения количества и типа корней квадратного уравнения. Основан на вычислении дискриминанта и его свойствах.
Иногда нахождение корней уравнений может быть сложной задачей, особенно для уравнений с высокой степенью или комплексными корнями. Однако, с использованием различных методов, можно достичь точного или приближенного решения уравнений.
Определение корня уравнения
Например, в уравнении x + 3 = 7 корнем будет число 4, так как при подстановке 4 вместо x получаем верное равенство: 4 + 3 = 7.
Определение корня уравнения тесно связано с понятием решения уравнения. Решение уравнения — это множество всех его корней. Если уравнение имеет более одного корня, то они образуют множество решений.
Существует несколько способов нахождения корней уравнений, в зависимости от типа уравнения. Некоторые из них включают алгебраические методы, методы графического анализа, итерационные методы и т.д. Выбор метода нахождения корней зависит от конкретной задачи и доступности вычислительных средств.
Определение корня уравнения является важным понятием в математике и находит широкое применение в различных областях, таких как физика, инженерия, экономика и другие.
Понятие корня уравнения
Например, в уравнении x^2 — 4 = 0 корнями будут числа 2 и -2, так как при подстановке этих значений вместо x уравнение превращается в 2^2 — 4 = 0 и (-2)^2 — 4 = 0, соответственно.
У уравнений может быть несколько корней или вовсе отсутствовать корни. Если уравнение не имеет решений, то оно называется бессмысленным или противоречивым.
Корни уравнения могут быть рациональными или иррациональными числами. Рациональные числа представляются дробью, в которой числитель и знаменатель являются целыми числами. Иррациональные числа, в отличие от рациональных, не могут быть представлены дробью и имеют бесконечнорасширяющуюся десятичную дробь без периода.
Существует множество способов нахождения корней уравнений, в зависимости от их формы и сложности. Один из таких способов — использование теоремы о корнях уравнения. Другие методы включают графический метод, метод подстановки, метод факторизации и т. д.
Понимание понятия корня уравнения является важным в математике и науках, где уравнения широко применяются для моделирования и решения различных проблем и задач.
Значимость корня уравнения
Значимость корня уравнения заключается в его способности решить задачи и проблемы, возникающие в различных областях науки и повседневной жизни.
Например, в физике корни уравнений могут представлять физические величины, такие как время, расстояние, скорость и другие. Они позволяют находить оптимальные параметры систем, решать задачи движения тел, изучать процессы в природе и т.д.
В экономике корни уравнений могут отражать оптимальные значения спроса и предложения, цены, доходности и другие экономические показатели. Они помогают предсказывать поведение рынка, прогнозировать изменения в экономике и принимать обоснованные решения в бизнесе.
В программировании корни уравнений могут использоваться для поиска и оптимизации алгоритмов. Они позволяют находить решения уравнений, определять условия и циклы выполнения программы, а также находить ошибки и устранять их.
Способы нахождения корня уравнения могут быть различными, в зависимости от типа и сложности уравнения. Они включают методы аналитического решения, численного решения, графического решения и другие.
Таким образом, корень уравнения играет важную роль в математике и ее приложениях. Он не только позволяет найти решения уравнений, но и обладает большой значимостью для научных и практических исследований.
| Примеры |
|---|
| Уравнение 2x + 3 = 7 имеет корень x = 2, который является решением данного уравнения. |
| Уравнение x^2 — 9 = 0 имеет корни x = -3 и x = 3, которые являются решениями данного уравнения. |
Примеры корней уравнений
- Уравнение 2x^2 — 5x + 2 = 0 имеет два корня: x1 = 0.5 и x2 = 2
- Уравнение x^2 + 4x + 4 = 0 имеет единственный корень: x = -2
- Уравнение x^2 — 9 = 0 имеет два корня: x1 = -3 и x2 = 3
- Уравнение x^2 + 7x + 10 = 0 имеет два корня: x1 = -2 и x2 = -5
- Уравнение 3x^2 + 2x — 1 = 0 имеет два корня: x1 ≈ -1.183 и x2 ≈ 0.516
Это только несколько примеров корней уравнений. В зависимости от вида уравнения (линейное, квадратное, кубическое и т. д.) и коэффициентов в нем, количество и тип корней может варьироваться. Чтобы найти корни уравнения, можно использовать различные методы, такие как метод квадратного уравнения, метод подстановки значений, метод графического представления и т. д.
Примеры одного корня уравнения
В математике корнем уравнения называется значение переменной, при котором уравнение выполняется. Уравнение может иметь различное количество корней, в том числе и один.
Примеры уравнений с одним корнем:
- Уравнение: x + 5 = 10. Исходное уравнение может быть переписано в виде x = 10 — 5, что дает значение x = 5. Значение 5 является корнем уравнения, так как при подстановке вместо x в исходное уравнение оно становится верным: 5 + 5 = 10.
- Уравнение: 2x — 3 = 7. Решим это уравнение, перенеся -3 на другую сторону: 2x = 7 + 3, тогда 2x = 10, а x = 10/2, что равно 5. Таким образом, значение 5 является корнем этого уравнения.
- Уравнение: x^2 — 4x + 4 = 0. Данное уравнение может быть факторизовано в виде (x — 2)(x — 2) = 0. Здесь видно, что оба множителя равны 0 при x = 2. Таким образом, значение 2 является корнем данного уравнения.
Таким образом, уравнение может иметь один корень, при котором само уравнение будет выполняться.
Примеры нескольких корней уравнения
Уравнение может иметь различное количество корней, в зависимости от его типа. Вот несколько примеров уравнений с несколькими корнями:
1. Квадратное уравнение:
Уравнение вида ax^2 + bx + c = 0, где a, b и c — коэффициенты, может иметь два корня. Например, рассмотрим уравнение x^2 — 5x + 6 = 0. Его корни будут x = 2 и x = 3.
2. Кубическое уравнение:
Уравнение вида ax^3 + bx^2 + cx + d = 0 может иметь три корня. Например, рассмотрим уравнение x^3 — 6x^2 + 11x — 6 = 0. Его корни будут x = 1, x = 2 и x = 3.
3. Тригонометрическое уравнение:
Уравнение вида sin(x) — cos(x) = 0 может иметь бесконечное количество корней. Например, рассмотрим уравнение sin(x) — cos(x) = 0. Его корни будут x = π/4 + 2πn и x = 5π/4 + 2πn, где n — целое число.
Это лишь несколько примеров уравнений с несколькими корнями. В зависимости от типа уравнения и его коэффициентов, количество и значения корней могут быть различными.
Вопрос-ответ:
Что такое корень уравнения?
Корнем уравнения называется значение переменной, при подстановке которого уравнение становится верным.
Как найти корень уравнения?
Существуют различные способы нахождения корня уравнения, в зависимости от его типа. Например, для линейного уравнения корнем будет значение, при котором переменная уравнения равна нулю.
Можно ли уравнение иметь несколько корней?
Да, уравнение может иметь один, несколько или даже бесконечное количество корней. Например, квадратное уравнение может иметь два, один или ни одного корня, в зависимости от дискриминанта.
Какие есть примеры уравнений?
Примеры уравнений могут быть разнообразными. Например, линейное уравнение: 2x + 3 = 7; квадратное уравнение: x^2 — 5x + 6 = 0; тригонометрическое уравнение: sin(x) = 0.5 и т.д.
Какое значение имеет корень уравнения?
Корень уравнения является решением задачи, которую оно описывает. Например, если уравнение моделирует движение тела, то корень уравнения будет соответствовать времени, в которое происходит событие или достигается определенное состояние.
Что называется корнем уравнения?
Корнем уравнения называется значение переменной, при подстановке которого в уравнение получается верное равенство.