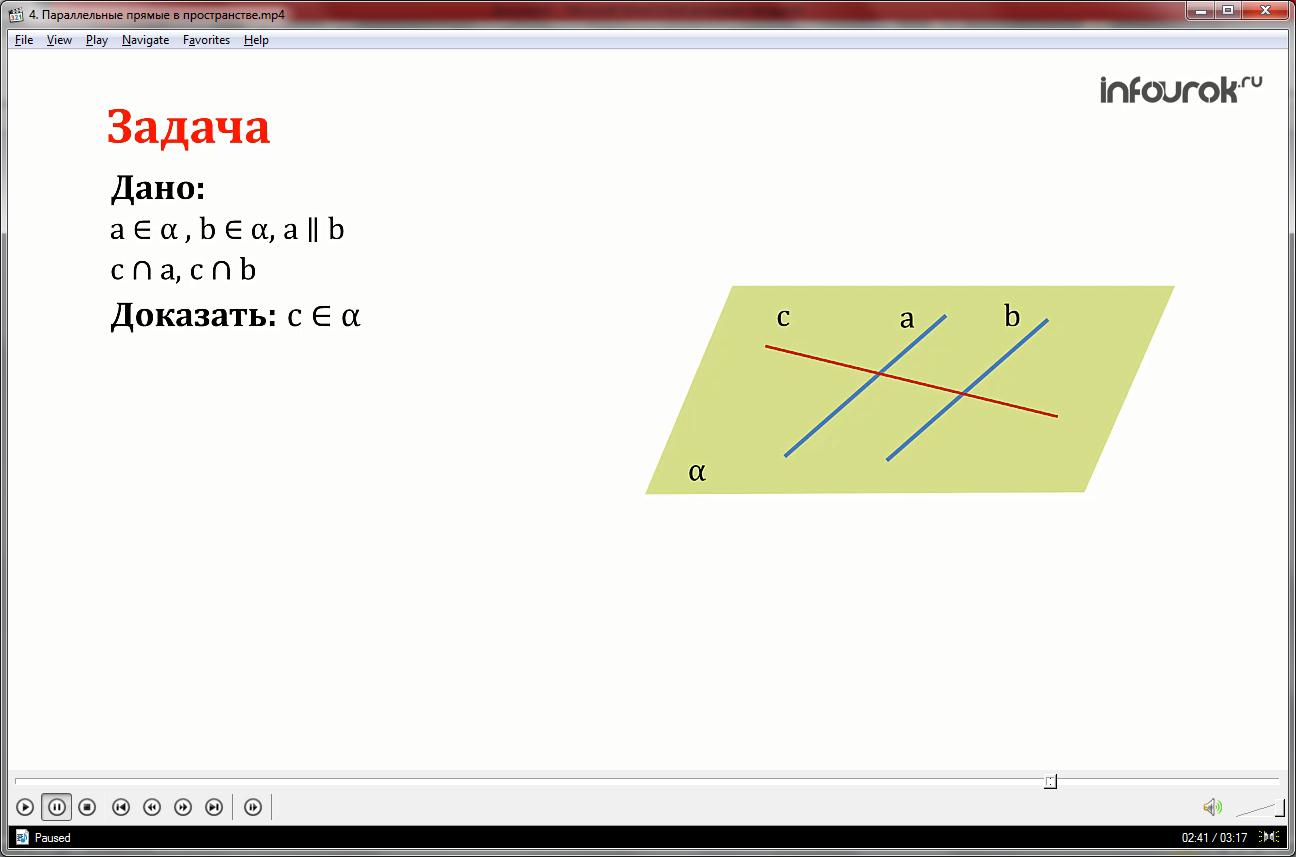
Параллельные прямые — это две прямые линии, которые никогда не пересекаются друг с другом. В пространстве, состоящем из трех измерений — длины, ширины и высоты, параллельные прямые сохраняют одинаковую дистанцию друг от друга на протяжении всего их пути.
Чтобы две прямые были параллельными, они должны находиться в одной плоскости и не иметь общих точек. Это означает, что если мы нарисуем две прямые линии на бумаге или поверхности, которая является плоскостью, и они никогда не пересекаются, то мы можем сказать, что они параллельны.
Параллельные прямые могут быть непосредственно расположены друг рядом с другом или удалены на значительное расстояние, но они все равно остаются параллельными. В геометрии это понятие является важным, так как оно помогает нам определить ориентацию объектов в пространстве и анализировать их взаимодействие.
Определение параллельных прямых в пространстве
Параллельными прямыми в пространстве называются прямые, которые лежат в плоскостях, параллельных друг другу. При этом, параллельные прямые не пересекаются ни в одной точке и расстояние между ними постоянно.
Для определения параллельности прямых в пространстве можно использовать следующие свойства:
- Свойство 1: Если две прямые пересекаются с третьей прямой так, что один из углов, образованных этими прямыми, является прямым углом, то они параллельны.
- Свойство 2: Если две прямые параллельны третьей прямой, то они параллельны и друг другу.
- Свойство 3: Если две прямые пересекают друг друга и образуют смежные углы, сумма которых равна 180 градусов, то они параллельны одной плоскости.
- Свойство 4: Если две прямые пересекаются с двумя параллельными прямыми и образуют смежные углы, сумма которых равна 180 градусов, то они параллельны друг другу.
Знание данных свойств позволяет установить параллельность прямых в пространстве, а также использовать данное понятие при решении задач геометрии и в других областях науки.
Что такое параллельные прямые?
Параллельные прямые имеют много важных свойств и применяются в различных областях. Например, в геометрии они используются для построения и изучения фигур, таких как параллелограммы и треугольники. В инженерии и архитектуре они используются для создания параллельных линий, которые применяются при построении зданий, дорог и других инфраструктурных объектов.
Для определения параллельности прямых можно использовать различные методы, включая аналитическую геометрию и геометрические конструкции. Например, если две прямые имеют одинаковый угол наклона, то они параллельны. Также параллельные прямые можно определить с помощью перпендикулярных линий или параллельных сторон фигур.
Параллельные прямые являются важным понятием в математике и находят применение во многих других науках и областях. Изучение и понимание их свойств помогает в решении различных задач и описании пространства.
Особенности параллельных прямых
Бесконечность
Параллельные прямые никогда не сходятся и не пересекаются. Они продолжаются в обе стороны в бесконечность.
Одна плоскость
Параллельные прямые всегда находятся в одной плоскости. Это значит, что они лежат на одной плоской поверхности и не отклоняются от нее.
Параллельные прямые находят широкое применение в геометрии и на практике. Они используются при построении и топографии, в архитектуре и дизайне, а также в технических и инженерных расчетах. Понимание особенностей параллельных прямых является важным для решения задач и создания точных конструкций.
Как определить параллельные прямые?
Существует несколько способов определить, являются ли прямые параллельными друг другу:
1. Визуальное сравнение
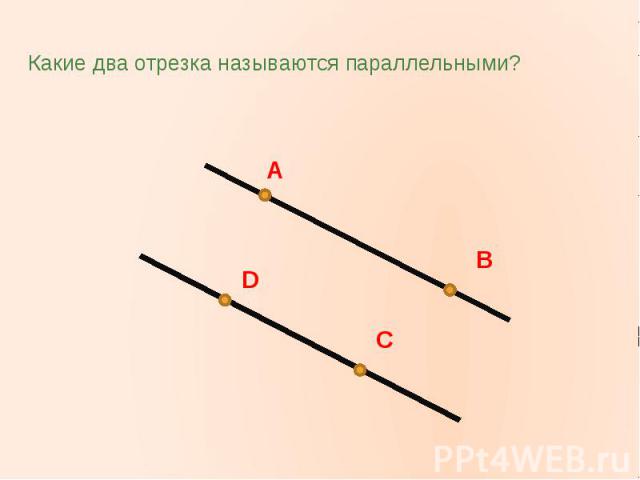
Этот способ самый простой и используется, когда прямые представлены на плоскости с помощью графического изображения. Если две прямые линии имеют одинаковый наклон и не пересекаются ни в одной точке, то они являются параллельными.
2. Использование углов
Другой способ — использование углов, образованных прямыми и третьей прямой, называемой трансверсальной. Если корреспондирующие углы (углы, расположенные по одну сторону трансверсальной линии и порождаемые двумя параллельными линиями) равны, то прямые параллельны.
Теперь вы знаете, как определить параллельные прямые. Это полезное знание для решения геометрических задач и построения различных фигур.
Условия параллельности прямых
Две прямые в пространстве называются параллельными, если они не пересекаются и не лежат в одной плоскости.
Существуют несколько способов определить параллельность прямых:
1. Критерий параллельности прямых

Две прямые параллельны, если угол между ними равен 0 градусов.
2. Расстояние между параллельными прямыми
Расстояние между двумя параллельными прямыми всегда постоянно и равно расстоянию между любыми их параллельными отрезками.
Для определения параллельности прямых можно использовать таблицу:
| Условия | Примеры |
|---|---|
| Прямые лежат в одной плоскости |  |
| Угол между прямыми равен 0 градусов |  |
| Расстояние между прямыми постоянно |  |
Зная эти условия, можно легко определить параллельность прямых в пространстве.
Система уравнений параллельных прямых
Две прямые в пространстве называются параллельными, если они не пересекаются и не сходятся в одну точку. Для определения параллельных прямых используется система линейных уравнений.
Система уравнений параллельных прямых имеет следующий вид:
l1: a1x + b1y + c1 = 0
l2: a2x + b2y + c2 = 0
Где l1 и l2 — прямые, a1, b1, c1, a2, b2, c2 — коэффициенты уравнений прямых.
Если прямые l1 и l2 параллельны, то левые части уравнений равны между собой, то есть:
a1 / a2 = b1 / b2 = c1 / c2
Таким образом, если система уравнений параллельных прямых имеет конкретные значения коэффициентов и выполняется равенство выше, то прямые являются параллельными.
Геометрическая интерпретация параллельных прямых
Для лучшего представления о параллельных прямых, понадобится визуализировать понятие плоскости. Представьте себе плоскость, как равномерную поверхность, не имеющую объема. Параллельные прямые как бы лежат в этой плоскости, никогда не скрещиваясь.
Однако, проиллюстрировать параллельные прямые в трехмерном пространстве бывает не так просто. На плоскости мы можем воспользоваться линейкой или карандашом, чтобы нарисовать параллельные линии. В трехмерном пространстве нам понадобится воображение и представления о различных плоскостях и углах.
Наиболее простым способом представления параллельных прямых на пространственном уровне является использование специальных символов и терминологии. В математике для обозначения параллельных линий, используют две параллельные стрелки: //$. Например, если прямая a параллельна прямой b, обозначается следующим образом: a //$ b.
Геометрическая интерпретация параллельных прямых помогает решать множество задач, связанных с построением объектов, определением плоскостей и углов, а также в практических приложениях, таких как проектирование зданий и дорог, систем координат и многое другое.
Примеры параллельных прямых
- Два равные прямых участка железнодорожных путей, проходящих вдоль друг друга.
- Две прямые, идущие одновременно вдоль рельефа горного склона.
- Параллельные стороны параллелограмма или квадрата.
- Линейные параллельные улицы в городских планах, которые не пересекаются.
- Параллельные линии широко используются в архитектуре, в проектировании и в строительстве.
Важно помнить, что параллельные прямые имеют одинаковое направление и не пересекаются ни в одной точке. Отсутствие пересечения является ключевым отличием параллельных прямых от скрещивающихся.
Вопрос-ответ:
Что такое параллельные прямые в пространстве?
Параллельными называются две прямые в пространстве, которые лежат в одной плоскости и не пересекаются.
Можете привести примеры параллельных прямых в пространстве?
Классическим примером параллельных прямых в пространстве являются железнодорожные пути. Каждая пара рельсов — это параллельные прямые.
Как определить, что две прямые параллельны в пространстве?
Две прямые параллельны в пространстве, если у них нет общих точек и они лежат в одной плоскости.
Что произойдет, если две прямые, которые были параллельны в пространстве, начнут пересекаться?
Если две прямые, которые были параллельны в пространстве, начнут пересекаться, это будет означать, что либо они не лежали в одной плоскости, либо они перестали быть прямыми.
Сколько параллельных прямых может быть в пространстве?
В пространстве может быть бесконечное количество параллельных прямых. Это связано с тем, что для определения параллельности двух прямых необходимо указать только одну плоскость, на которой они лежат.
Что такое параллельные прямые в пространстве?
Параллельные прямые в пространстве — это две прямые, которые лежат в разных плоскостях, но не пересекаются ни в одной точке.