В математике и анализе, первообразная функция – это одна из основных понятий, которое активно используется для решения дифференциальных уравнений. Это понятие является ключевым для понимания процесса интегрирования и нахождения площади под графиком функции.
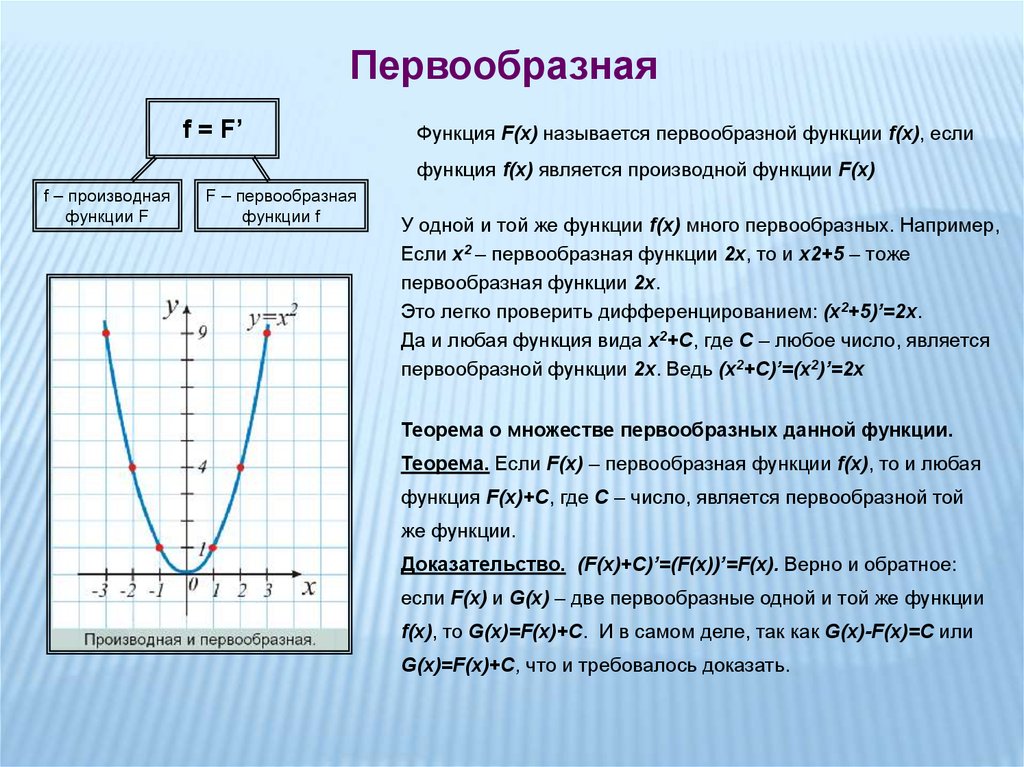
Первообразная функция – это функция, производная от которой равна данной функции. В математической терминологии первообразная функция также называется антипроизводной. Общий подход к поиску первообразной функции заключается в обратном процессе к поиску производной функции.
Для того чтобы найти первообразную функцию, необходимо найти все ее открытые интервалы, на которых производная функции существует и непрерывна, а затем найти функцию, производная которой будет равна данной функции на всех этих интервалах. Первообразная функция определена с точностью до добавления константы, так как производная от константы равна нулю
Знание концепции первообразной функции не только позволяет решать дифференциальные уравнения и находить площади под графиками функций, но и имеет множество практических применений в различных областях, таких как физика, экономика, статистика и другие. Математика и анализ опираются на понимание первообразной функции как одного из основных понятий, необходимых для понимания более сложных математических концепций и применений.
Что такое первообразная функция
То есть, если производная f(x) существует для всех точек из некоторого интервала, то существует такая функция F(x), производная которой равна f(x). В этом случае говорят, что F(x) – первообразная функция для функции f(x).
Первообразная функция имеет важное значение в теории дифференциального исчисления и интегральных уравнений. Зная первообразную функцию для заданной функции f(x), можно решать различные задачи, связанные с исходной функцией.
Необходимо отметить, что первообразная функция может отличаться от другой первообразной функции для той же функции f(x) на некоторую константу. Это связано с тем, что первообразная функция определена с точностью до аддитивной константы, так как производная постоянной равна нулю.
Для нахождения первообразной функции для заданной f(x) используется процесс интегрирования. Он позволяет найти общий вид первообразной функции, включающий все возможные функции, отличающиеся друг от друга на константу.
Интегрирование – это обратный процесс дифференцирования. Для его выполнения существуют особые методы и правила, которые позволяют находить первообразную функцию для большого множества функций.
Определение первообразной функции
Первообразной функции называется функция, производная которой равна исходной функции. Другими словами, первообразная функция F(x) функции f(x) обладает свойством F'(x) = f(x), где символ F'(x) обозначает производную функции F(x) по переменной x.
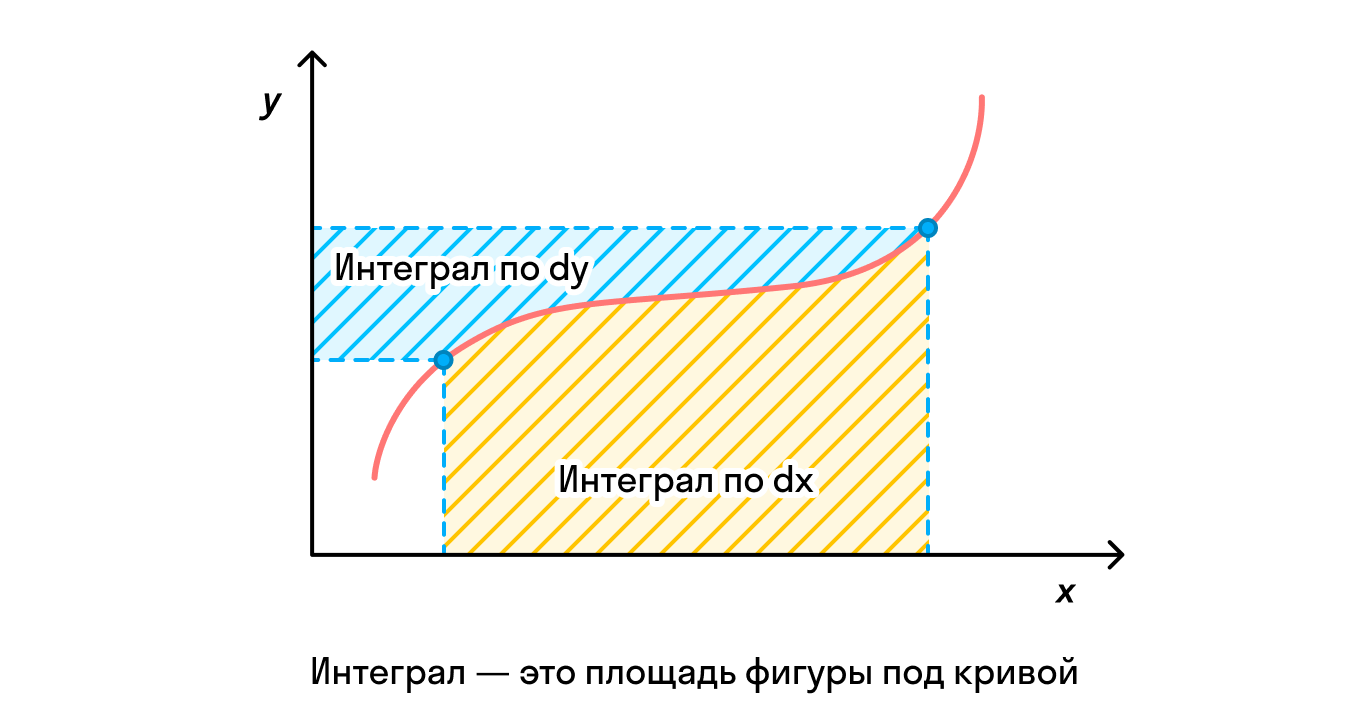
Свойство первообразной функции позволяет найти значение определенного интеграла функции f(x) на заданном интервале [a, b]. Точнее, если F(x) — первообразная функции f(x), то значение определенного интеграла функции f(x) на интервале [a, b] можно вычислить с помощью формулы:
∫ab f(x) dx = F(b) — F(a)
Знание первообразной функции позволяет решать уравнения, связанные с нахождением площади под графиком функции или определенного интеграла функции на заданном интервале. Однако, следует учитывать, что первообразная функции не единственна, и для каждой функции может существовать бесконечное количество первообразных, отличающихся на константу.
Свойства первообразной функции
Важными свойствами первообразной функции являются:
- Линейность: первообразная функция линейна, то есть справедливо свойство $\int (af(x) + bg(x))\,dx = a\int f(x)\,dx + b\int g(x)\,dx$.
- Интеграл от производной: интеграл от производной функции равен самой функции, то есть $\int f'(x)\,dx = f(x) + C$, где $C$ – константа интегрирования.
- Замена переменной: при замене переменной в интеграле происходит изменение границ интегрирования и подынтегральной функции.
- Интегрирование по частям: позволяет вычислить интеграл от произведения двух функций.
- Таблица интегралов: существует таблица известных интегралов, которая позволяет быстро находить первообразное от многих функций.
Таким образом, понимание свойств первообразной функции позволяет упростить процесс нахождения интегралов и решение различных математических задач.