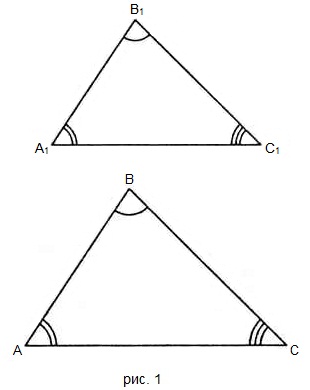
Подобие треугольников — это основное понятие в геометрии, которое играет важную роль при решении различных задач. Подобные треугольники имеют равные углы и пропорциональные стороны, что делает их однотипными и позволяет применять определенные законы и формулы для их решения.
Существует два основных типа подобных треугольников: треугольники, у которых все углы равны между собой, и треугольники, у которых только два угла равны. В обоих случаях треугольники имеют пропорциональные стороны и подобные формы, но различаются по количеству равных углов.
Понимание подобия треугольников позволяет применять различные методы и приемы для решения геометрических задач, связанных с треугольниками. Например, на основе подобия треугольников можно находить пропорциональные стороны или использовать теорему Пифагора для нахождения недостающих значений.
Важно отметить, что подобие треугольников не зависит от их размеров и может быть применено как для маленьких, так и для больших треугольников. Это открывает широкие возможности в применении их в различных задачах, как в школьной математике, так и в профессиональной геометрии.
Подобные треугольники: основные определения и свойства
Определение подобных треугольников
Для формального определения подобных треугольников используется условие подобия. Для двух треугольников АВС и ХУZ условием подобия является равенство отношений их сторон:
- AB / HX = AC / HY = BC / HZ
Если данное условие выполняется, то треугольники АВС и ХУZ считаются подобными.
Свойства подобных треугольников

Подобные треугольники обладают рядом важных свойств:
- Соответствующие углы подобных треугольников равны. То есть, если в треугольнике АВС угол А равен углу Х в треугольнике ХУZ, то угол В будет равен углу У, и угол С будет равен углу Z.
- Соответствующие стороны подобных треугольников пропорциональны. Это означает, что отношение длин двух сторон в одном треугольнике равно отношению длин соответствующих сторон в другом треугольнике.
- Если два треугольника подобны, то их площади также пропорциональны. Исходя из этого свойства, можно сказать, что отношение площадей двух подобных треугольников равно квадрату отношения длин их сторон.
Понимание основных определений и свойств подобных треугольников играет важную роль в геометрии и налаживает базу для изучения более сложных понятий и задач.
Определение подобных треугольников
Два треугольника называют подобными, если они имеют равные углы. Определение подобности треугольников базируется на теореме угловых соответствий.
Теорема угловых соответствий гласит, что если в двух треугольниках соответственно равны углы при их вершинах, то эти треугольники подобны.
Подобные треугольники имеют пропорциональные стороны. Это означает, что соответствующие стороны в подобных треугольниках имеют одинаковые отношения.
Для подобных треугольников применяются обозначения. Пусть треугольник AВС подобен треугольнику DEF, тогда записывается: AВС ~ DEF.
Определение подобных треугольников часто используется в геометрии для решения задач, связанных с нахождением неизвестных сторон или углов треугольника. Подобные треугольники позволяют упростить расчеты и сделать задачу более понятной.
| Условия подобия треугольников ABC и DEF: | Равные углы: | |
|---|---|---|
| Угол A = Угол D | Угол B = Угол E | Угол C = Угол F |
Определение подобных треугольников является важным базовым понятием в геометрии и находит применение в различных областях, например в архитектуре, строительстве и дизайне.
Условия подобия треугольников
Два треугольника называют подобными, если выполняются следующие условия:
| 1. | Углы при соответствующих вершинах треугольников равны. |
| 2. | Соотношение длин сторон треугольников соответствует. |
То есть, если два треугольника имеют равные углы при соответствующих вершинах, а также отношение длин их сторон одинаково, то они считаются подобными.
Как найти подобные треугольники
Два треугольника называют подобными, если у них соответственные углы равны, а соответствующие стороны пропорциональны. Найти подобные треугольники можно, применив следующие методы:
1. Угловые признаки: Для определения подобия двух треугольников можно проверить, равны ли у них соответственные углы. Если все углы первого треугольника равны соответствующим углам второго треугольника, то треугольники подобны.
2. Пропорциональность сторон: Если у трех сторон первого треугольника соответственно есть три стороны второго треугольника, причем отношение длин соответствующих сторон одного треугольника к соответствующим сторонам другого треугольника одинаково, то треугольники подобны.
Важно помнить, что подобные треугольники могут иметь одинаковые формы, но разные размеры. Определение подобных треугольников является важным инструментом в геометрии, поскольку позволяет использовать законы подобия для решения различных задач.
Соотношения сторон подобных треугольников
Таким образом, если треугольники ABC и DEF подобны, то соответствующие стороны этих треугольников имеют следующие соотношения:
| ABC | DEF |
|---|---|
| AB | DE |
| BC | EF |
| AC | DF |
Например, если AB/DE = BC/EF = AC/DF, то треугольники ABC и DEF подобны.
Зная соотношение сторон подобных треугольников, можно вычислить значения некоторых сторон, если известны значения других. Это свойство подобных треугольников широко используется в геометрии для решения различных задач.
Соотношения высот подобных треугольников
Подобные треугольники имеют одинаковые углы и пропорциональные стороны. Следовательно, соотношения высот подобных треугольников тоже будут сохраняться.
Если два треугольника подобны, то отношение высот одного треугольника к высотам другого будет равно отношению сторон этих треугольников.
Следующие соотношения высот можно применить для подобных треугольников:
- Высота одного треугольника к высоте другого равна отношению длины сторон двух треугольников;
- Высота одного треугольника к длине соответствующей стороны другого треугольника равна отношению длины высоты двух треугольников;
- Высота одного треугольника к длине соответствующей стороны другого треугольника равна отношению длины высоты oдного треугольника к длине высоты другого треугольника.
Таким образом, соотношения высот подобных треугольников позволяют нам определить соотношения между сторонами и высотами треугольников при проведении подобия.
Соотношения биссектрис подобных треугольников
Биссектрисы подобных треугольников делят стороны треугольника в таком же соотношении, в котором делят углы треугольника.
Например, если два треугольника подобны, то соотношение биссектрис будет равно соотношению сторон треугольников в данном соответствии.
Следуя этим соотношениям, можно вычислить длину одной стороны треугольника, зная длины других сторон и значения соотношений биссектрис.
Таким образом, знание соотношений биссектрис позволяет проводить вычисления в подобных треугольниках и находить неизвестные значения длин сторон.
Подобие треугольников в геометрическом моделировании
Критерии подобия треугольников
Подобие треугольников определяется существованием трех соответствующих равных углов, а также пропорциональности длин противолежащих сторон. При этом, углы могут быть как прямыми, так и непрямыми.
Формулы для определения подобия треугольников:
1. Для равенства углов:
- Равенство одного угла обозначается символом ≡ (например, ∠ABC ≡ ∠DEF)
- Если все углы одного треугольника равны соответствующим углам другого треугольника, то треугольники называются подобными.
2. Для пропорциональности сторон:
- Пропорциональные стороны обозначаются знаком ∝ (например, AB ∝ DE)
- Если соответствующие стороны двух треугольников пропорциональны, то треугольники подобны.
Примеры применения подобия треугольников в геометрическом моделировании
Подобие треугольников используется в различных областях геометрического моделирования, таких как:
- Архитектура: подобие треугольников позволяет строить модели зданий и сооружений, учитывая пропорциональные отношения;
- Геодезия и картография: подобие треугольников используется для измерения и построения карт;
- Компьютерная графика: подобие треугольников применяется для создания трехмерных объектов и анимаций;
- Машиностроение и авиастроение: подобие треугольников используется для расчета прочностных характеристик, проектирования и моделирования;
- Медицина: подобие треугольников используется для моделирования органов и тканей в рамках медицинского визуализации и симуляции.
Таким образом, понимание и применение подобия треугольников является неотъемлемой частью геометрического моделирования и находит широкое применение в различных сферах человеческой деятельности.
| № | Пример | Описание |
|---|---|---|
| 1 |  | Пример применения подобия треугольников в архитектуре |
| 2 |  | Пример применения подобия треугольников в компьютерной графике |
| 3 |  | Пример применения подобия треугольников в медицине |
Примеры практического применения подобия треугольников

1. Построение карт на основе аэрофотоснимков
Когда необходимо создать карту большой территории, инженеры используют аэрофотоснимки, полученные с помощью специальных камер, установленных на самолетах или дронов. Далее нужно определить координаты объектов на фотографиях для их правильного отображения на карте. Подобие треугольников применяется для нахождения координат и размеров объектов на основе измерений треугольников на фотографиях.
2. Определение высоты объектов
Подобие треугольников также используется при определении высоты объектов, которая не может быть измерена напрямую. Например, чтобы измерить высоту высокой башни или горы, можно использовать нашатырную линию и отложить на ней измерения отношений высоты объекта к длине его тени. Затем, используя подобие треугольников, можно определить высоту объекта.
Вышеуказанные примеры демонстрируют практическое применение подобия треугольников в реальном мире. Это лишь некоторые из множества возможностей применения этого свойства треугольников, что подчеркивает его важность и полезность.
Вопрос-ответ:
Что такое подобные треугольники?
Подобными треугольниками называются такие треугольники, которые имеют одинаковые углы.
В чем основное условие подобия треугольников?
Основное условие подобия треугольников заключается в том, что соответствующие углы данных треугольников должны быть равными.
Что происходит с пропорциональными сторонами при подобии треугольников?
При подобии треугольников, пропорциональные стороны треугольников остаются пропорциональными.
Какое свойство имеют соответствующие высоты подобных треугольников?
Соответствующие высоты подобных треугольников тоже подобны, и их длины образуют пропорциональные отношения с соответствующими сторонами треугольников.
Какие два треугольника называют подобными?
Два треугольника называют подобными, если углы одного треугольника равны соответствующим углам другого треугольника.