
Многоугольники – это фигуры с прямыми сторонами и углами, состоящие из двух или более отрезков. В зависимости от количества сторон, многоугольники могут иметь разные названия: треугольники, четырехугольники, пятиугольники и так далее.
Однако, не все многоугольники равноценны друг другу. Некоторые из них обладают особыми свойствами, которые делают их уникальными. Многоугольники, у которых все стороны и все углы равны между собой, называются правильными.
Как правило, правильные многоугольники имеют специальные названия. Например, треугольник с равными сторонами и углами называется равносторонним треугольником. Четырехугольник, у которого все стороны и углы равны, является равнобоким прямоугольником. У пятиугольника, справедливость таких же равенств, уже нет, он может быть правильным или неправильным.
Понятие и определение
Среди правильных многоугольников особо известны правильные треугольники (равносторонние треугольники), квадраты, правильные пятиугольники (пентагоны), правильные шестиугольники (гексагоны), правильные восмиугольники (октагоны) и прочие.
Основные характеристики правильных многоугольников:
- Сторона – равное расстояние между двумя вершинами многоугольника. В правильном многоугольнике все стороны одинаковы.
- Угол – область между двумя сторонами многоугольника. В правильном многоугольнике все углы одинаковы.
- Вершина – точка пересечения сторон многоугольника. В правильном многоугольнике все вершины одинаковы.
Изучение правильных многоугольников имеет большое значение в геометрии и математике в целом, так как они являются основой для многих конструкций и доказательств.
Правильные многоугольники
Самым известным примером правильного многоугольника является равносторонний треугольник, у которого все стороны и углы равны. Он имеет три стороны и три угла, каждый из которых равен 60 градусов.
Другим примером правильного многоугольника является квадрат. У него четыре стороны и четыре угла, каждый равный 90 градусов.
Существуют также правильные многоугольники с большим числом сторон. Например, пятиугольник (пентагон), шестиугольник (гексагон), семиугольник (гептагон) и т.д. У каждого из них все стороны и углы равны.
Особая роль в геометрии принадлежит правильным многоугольникам, которые обладают особыми свойствами. Например, правильный пятиугольник нельзя построить с помощью циркуля и линейки, но его можно построить с использованием компаса.
| Название | Число сторон | Число углов | Сумма углов |
|---|---|---|---|
| Треугольник | 3 | 3 | 180° |
| Квадрат | 4 | 4 | 360° |
| Пятиугольник (Пентагон) | 5 | 5 | 540° |
| Шестиугольник (Гексагон) | 6 | 6 | 720° |
| Семиугольник (Гептагон) | 7 | 7 | 900° |
Особенности правильных многоугольников
Правильным многоугольником называется многоугольник, все стороны и углы которого равны между собой. Они обладают несколькими интересными и важными особенностями, которые делают их особенными и уникальными.
Равные стороны
В правильном многоугольнике все стороны равны между собой. Это позволяет ему иметь симметричную форму и одинаковые длины всех сторон. Благодаря этому особенному свойству, правильные многоугольники легко распознаваемы и часто используются в архитектуре, геометрии и других областях.
Углы
Каждый угол в правильном многоугольнике равен другому углу внутри этого же многоугольника. Таким образом, если известна мера одного угла, легко можно определить меру всех остальных углов. Благодаря этому свойству, правильные многоугольники являются полноценными и симметричными фигурами с угловыми свойствами, которые можно легко изучить и использовать в различных математических и геометрических рассуждениях.
Заметка: В правильных многоугольниках не только равны все стороны и углы, но также равны все диагонали (отрезки, соединяющие вершины многоугольника, не являющиеся его сторонами). Это еще одна интересная особенность, которая делает правильные многоугольники уникальными и важными для изучения.
Виды правильных многоугольников
| Название | Количество сторон | Количество углов |
|---|---|---|
| Треугольник | 3 | 3 |
| Квадрат | 4 | 4 |
| Пятиугольник | 5 | 5 |
| Шестиугольник | 6 | 6 |
| Семиугольник | 7 | 7 |
| Восьмиугольник | 8 | 8 |
| Девятиугольник | 9 | 9 |
| Десятиугольник | 10 | 10 |
Каждый следующий правильный многоугольник имеет на одну сторону и один угол больше, чем предыдущий. При этом все стороны остаются равными, а все углы — равными.
Правильные многоугольники находят широкое применение в различных областях, таких как геометрия, архитектура, рисование и дизайн. Их равномерная и симметричная форма делает их эстетически привлекательными и удобными в использовании.
Равносторонний треугольник
Из-за своей симметрии, равносторонний треугольник имеет особенные свойства:
Свойства равностороннего треугольника:
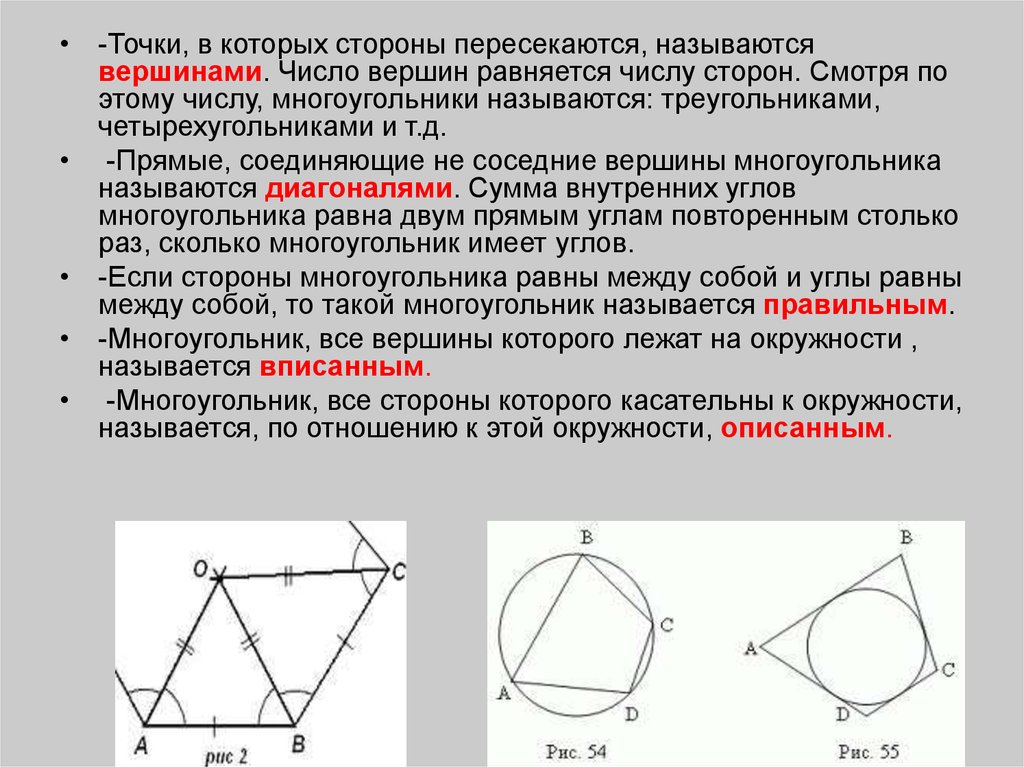
- В равностороннем треугольнике все стороны имеют одинаковую длину.
- Все углы равностороннего треугольника равны 60 градусов.
- Высота, проведенная из вершины равностороннего треугольника, является биссектрисой и медианой одновременно.
- Перпендикуляр, опущенный из вершины равностороннего треугольника на его основание, делит основание на две равные части.
- Окружность, описанная около равностороннего треугольника, проходит через все его вершины.
- Окружность, вписанная в равносторонний треугольник, касается всех его сторон и имеет радиус, равный половине длины стороны треугольника.
Равносторонний треугольник является одним из наиболее простых и регулярных многоугольников, который часто встречается в геометрии и используется в различных математических задачах и конструкциях.
Квадрат
Свойства квадрата:
- Все стороны квадрата равны между собой.
- Все углы квадрата равны 90 градусов.
- Диагонали квадрата равны друг другу и перпендикулярны.
- Одна из диагоналей квадрата является его осью симметрии.
Квадрат является одним из самых простых и наиболее известных многоугольников. Из-за своих свойств и геометрической простоты, квадрат часто используется в различных областях науки, инженерии и искусства.
Правильный пятиугольник
Правильный пятиугольник можно построить с помощью циркуля и линейки. Для этого необходимо провести окружность с центром в точке O и радиусом OA, где O — центр окружности, а A — одна из вершин пятиугольника. Затем провести линию, соединяющую каждую вершину пятиугольника с центром O. В результате получится правильный пятиугольник.
Правильные пятиугольники обладают рядом интересных свойств. Например, сумма всех внутренних углов правильного пятиугольника равна 540 градусов. Также, длина окружности, описанной вокруг правильного пятиугольника, составляет пять длин его сторон.
Правильные пятиугольники встречаются в различных областях науки и искусства. Например, они используются в архитектуре, математике и дизайне. Также, существуют различные символические значения, приписываемые правильным пятиугольникам в различных культурах и религиях.
Важно отметить, что правильные пятиугольники не могут быть построены с помощью компаса и линейки. Это было доказано великим математиком Карлом Фридрихом Гауссом в 19 веке.
Правильный шестиугольник
Правильный шестиугольник также называется гексагоном. Он является одним из трех правильных многоугольников, вместе с правильным треугольником и правильным четырехугольником (квадратом).
Свойства правильного шестиугольника:
- Равные стороны: Все шесть сторон правильного шестиугольника имеют одинаковую длину. Как результат, все шестиугольники равны.
- Равные углы: Угол между любыми двумя сторонами правильного шестиугольника равен 120 градусам. Все шестиугольники имеют одни и те же углы.
- Внутренние углы: Внутренние углы правильного шестиугольника составляют 720 градусов. В сумме все углы внутри шестиугольника образуют 720 градусов.
- Симметрия: У правильного шестиугольника есть несколько осей симметрии, проходящих через его центр и соединяющих противоположные вершины. Это означает, что его форма выглядит одинаково при повороте на 60, 120 и 180 градусов.
Правильные шестиугольники широко используются в различных областях, таких как архитектура, математика и игры. Их симметричная и красивая форма делает их привлекательными для использования в дизайне и искусстве.
Вопрос-ответ:
Какие многоугольники называются правильными?
Правильными называются многоугольники, у которых все стороны одинаковой длины и все углы равны.
Что такое правильный треугольник?
Правильный треугольник — это треугольник, у которого все стороны равны и все углы равны 60 градусов.
Какие еще многоугольники могут быть правильными?
Правильными многоугольниками могут быть четырехугольники (квадрат), пятиугольники (пентагон), шестиугольники (гексагон) и так далее. Все они имеют равные стороны и равные углы.
Каковы свойства правильных многоугольников?
У правильных многоугольников все стороны равны, все углы равны, центром правильного многоугольника является точка, равноудаленная от всех вершин. Также в правильном многоугольнике каждая диагональ является радиусом вписанной окружности и кратна числу вершин минус 2.
В каких областях применяются правильные многоугольники?
Правильные многоугольники имеют множество применений в разных областях. Например, они широко используются в геометрии, для построения и изучения различных фигур. Также правильные многоугольники встречаются в архитектуре, дизайне, химии и даже в природе — многие кристаллы имеют правильную многоугольную форму.
Что такое правильный многоугольник?
Правильный многоугольник — это многоугольник, у которого все стороны равны между собой, а все углы также равны.