Синус угла — одна из основных тригонометрических функций, описывающая отношение противоположной стороны треугольника к гипотенузе. Открытый вопрос для многих студентов — как найти значение синуса угла в пределах от 0 до 180 градусов. Давайте разберемся.
Первым шагом является определение угла в градусах. Для этого можно использовать угломер или формулу для перевода радиан в градусы. Затем необходимо определить соответствующие отношения сторон треугольника в соответствии с заданным углом.
Рассмотрим пример нахождения синуса угла величиной 45 градусов. Из начала координат проводим отрезок длиной 1 единица вправо и находящийся под углом 45 градусов. Этот отрезок служит гипотенузой прямоугольного треугольника, поскольку высота равна 1, а основание равно √2.
Используя определение синуса (отношение противоположной стороны к гипотенузе), можно найти значение синуса угла 45 градусов: sin(45°) = 1/√2 = √2/2. Таким образом, синус 45 градусов равен √2/2.
Для нахождения синуса углов в пределах от 0 до 180 градусов можно использовать таблицу синусов или калькулятор с тригонометрическими функциями. Важно помнить, что синус угла \theta в круге радиуса R также определяется координатой точки, находящейся на окружности радиуса R и отстоящей от начала координат на угол \theta. Таким образом, синус любого угла можно найти и с помощью данного определения.
Синус угла и его нахождение
Для нахождения синуса угла в пределах от 0 до 180 градусов, можно воспользоваться таблицей тригонометрических значений или специальным калькулятором. Также можно применить следующую формулу:
sin(угол) = противолежащий катет / гипотенуза
Также стоит отметить, что синус угла имеет периодичность 360 градусов и поэтому для углов, больших 180 градусов, следует использовать дополнительные математические преобразования.
Значения синуса угла расположены на интервале от -1 до 1. Например, для угла 30 градусов синус будет равен 0.5, а для угла 90 градусов — единице.
Познакомившись с концепцией синуса угла и способами его нахождения в пределах от 0 до 180 градусов, вы сможете применять его в решении различных задач и проблем, связанных с геометрией и физикой.
Что такое синус угла?
Синус угла может принимать значения от -1 до 1, и его значение зависит от величины угла. Если угол равен 90 градусов, то синус угла будет равен 1. Если угол равен 0 градусов, то синус угла будет равен 0. Если угол равен 180 градусов, то синус угла будет равен -1. Значения синуса угла в промежутке от 0 до 90 градусов являются положительными, а значения синуса угла в промежутке от 90 до 180 градусов являются отрицательными.
Синус угла имеет много применений в математике и науке, особенно в геометрии, физике и инженерии. Он используется для решения задач, связанных со сторонами и углами треугольников, а также для моделирования периодических явлений, таких как звуковые и электромагнитные волны.
Определение и связь с геометрией
Геометрическое определение синуса заключается в следующем: синус угла равен отношению противолежащей стороны треугольника к гипотенузе.
Это означает, что если у нас есть прямоугольный треугольник, в котором угол А находится напротив стороны a, а гипотенуза обозначается как h, то синус угла А может быть выражен следующей формулой: sin(A) = a/h.
Синус угла также может быть выражен с использованием длин двух сторон треугольника, не являющихся гипотенузой:
- sin(A) = a/c, если a является противолежащей стороной угла А и c — гипотенузой
- sin(A) = b/c, если b является острым углом
Знание синуса угла и его связи с геометрией позволяет решать множество задач, связанных с треугольниками и углами. Он также является одним из основных элементов тригонометрии и используется в различных научных и технических областях, включая физику, инженерию и компьютерную графику.
Математическая формула синуса
- Для угла в градусах: sin(α) = P/O,
- Для угла в радианах: sin(α) = P/O,
Где sin(α) — значение синуса угла α, P — длина противолежащего катета, O — длина гипотенузы. Обратите внимание, что в данной формуле показано соотношение для прямоугольного треугольника. Если мы имеем дело с другими типами треугольников или углами, формулы могут отличаться.
Используя данную математическую формулу, можно вычислить значение синуса угла в пределах от 0 до 180 градусов. Значение синуса угла всегда будет находиться в интервале от -1 до 1. Например, если угол α равен 45 градусам, то синус этого угла будет равен √2/2, что примерно равно 0.707.
График функции синуса
На графике функции синуса можно наблюдать основные характеристики этой функции:
- Периодичность: функция синуса имеет период равный 2π. Это означает, что график повторяется через каждые 2π радиан (или 360 градусов).
- Амплитуда: амплитуда графика синуса определяется максимальным значением, которое функция может принимать. Для функции синуса амплитуда равна 1.
- Максимумы и минимумы: график функции синуса имеет максимумы и минимумы в точках, где значение синуса равно 1 или -1 соответственно.
- Симметрия: график функции синуса симметричен относительно начала координат.
Для построения графика функции синуса можно использовать таблицу значений. Ниже приведена таблица значений функции синуса для углов от 0 до 180 градусов:
| Угол (градусы) | Значение синуса |
|---|---|
| 0 | 0 |
| 30 | 0.5 |
| 45 | 0.707 |
| 60 | 0.866 |
| 90 | 1 |
| 120 | 0.866 |
| 135 | 0.707 |
| 150 | 0.5 |
| 180 | 0 |
Используя эти значения, можно построить график функции синуса в пределах от 0 до 180 градусов. График будет иметь форму плавной кривой, которая повторяется через каждые 180 градусов.
Как найти синус угла в пределах от 0 до 180 градусов?
В пределах от 0 до 180 градусов синус угла можно найти, используя соответствующую таблицу или калькулятор. Также можно использовать специальную формулу:
| Угол (градусы) | Синус угла |
|---|---|
| 0° | 0 |
| 30° | 0.5 |
| 45° | 0.707 |
| 60° | 0.866 |
| 90° | 1 |
| 120° | 0.866 |
| 135° | 0.707 |
| 150° | 0.5 |
| 180° | 0 |
Например, для угла 45° синус угла будет равен 0.707. Эта информация может быть полезна при решении различных задач, связанных с геометрией, физикой и другими науками.
Кроме того, существует также формула для вычисления синуса угла через противоположную и гипотенузу прямоугольного треугольника:
sin(угол) = противоположная сторона / гипотенуза
Эта формула может быть использована для вычисления синуса угла в любом прямоугольном треугольнике.
Таблицы синусов основных углов
Таблица синусов основных углов позволяет нам быстро и легко получить значение синуса для углов 0°, 30°, 45°, 60° и 90°. Эти углы являются особыми и достаточно часто встречаются в различных задачах и вычислениях.
Значение синуса для каждого из этих углов:
Угол 0°: sin(0°) = 0
Угол 30°: sin(30°) = 1/2
Угол 45°: sin(45°) = √2/2
Угол 60°: sin(60°) = √3/2
Угол 90°: sin(90°) = 1
Эти значения помогают нам быстро решать различные задачи с использованием синуса угла и облегчают вычисления в тригонометрии.
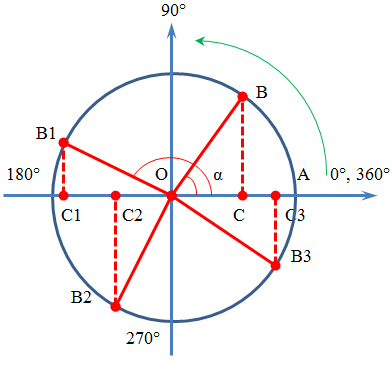
Использование тригонометрического круга
Чтобы использовать тригонометрический круг для нахождения значения синуса угла, найдите угол на круге и обратите внимание на соответствующую точку (x, y) на круге. Значение синуса будет равно координате y этой точки.
Например, если угол равен 30 градусам, то найдите точку на круге, где линия угла 30 градусов пересекает круг. Затем найдите соответствующую координату y этой точки и это будет значение синуса угла 30 градусов.
Тригонометрический круг также помогает в нахождении значения косинуса и тангенса угла. Значение косинуса равно координате x точки на круге, а значение тангенса равно отношению синуса к косинусу.
Таблица ниже показывает значения синуса, косинуса и тангенса некоторых углов в пределах от 0 до 180 градусов, которые могут быть использованы при работе с тригонометрическим кругом:
| Угол (градусы) | Синус | Косинус | Тангенс |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| 30 | 0.5 | 0.866 | 0.577 |
| 45 | 0.707 | 0.707 | 1 |
| 60 | 0.866 | 0.5 | 1.732 |
| 90 | 1 | 0 | ∞ |
Использование тригонометрического круга позволяет легко находить значения синуса, косинуса и тангенса угла в пределах от 0 до 180 градусов, и это очень полезно при решении задач из различных областей, таких как физика и инженерия.
Формула синуса с помощью треугольников
Формула синуса позволяет вычислить значение синуса угла при известных длинах сторон треугольника. Для этого необходимо знать длину противоположного катета и гипотенузы.
Формула синуса выглядит следующим образом:
sin A = a / c
Где:
sin A— значение синуса угла Aa— длина противоположного катетаc— длина гипотенузы
Чтобы найти значение синуса угла с помощью формулы синуса, необходимо знать длину противоположного катета и гипотенузы и применить формулу.
Например:
- Если длина противоположного катета равна 4, а длина гипотенузы равна 5, то значение синуса угла будет:
sin A = 4 / 5sin A = 0.8
Таким образом, с помощью формулы синуса и известных длин сторон треугольника можно найти значение синуса угла в пределах от 0 до 180 градусов.
Вопрос-ответ:
Что такое синус угла?
Синус угла — это отношение противолежащего катета прямоугольного треугольника к гипотенузе. Он является одним из тригонометрических соотношений и показывает, насколько далеко отрезок противолежащего катета от направления гипотенузы.
Как найти синус угла?
Для нахождения синуса угла нужно разделить длину противолежащего катета на длину гипотенузы прямоугольного треугольника. Обрати внимание, что значения синуса угла находятся в пределах от -1 до 1.
Как найти значение синуса угла в пределах от 0 до 180 градусов?
Для нахождения значения синуса угла в пределах от 0 до 180 градусов можно использовать таблицы значений тригонометрических функций или калькулятор с функцией синуса. Также можно использовать формулу синуса для преобразования угла в радианы и нахождения значения синуса.
Как понять, какую из значений синуса угла использовать из таблицы постоянных или сменных значений?
Если значение угла находится в пределах от 0 до 90 градусов, следует использовать значения синуса из таблицы постоянных значений. Если угол находится в пределах от 90 до 180 градусов, нужно использовать таблицу сменных значений, где синус угла будет отрицательным. Например, sin(30°) = 0.5, а sin(150°) = -0.5.