
Вектор – это величина, которая имеет не только числовую характеристику, но и определенное направление и точку приложения. Он обычно представляется стрелкой, начало которой указывает на точку исхода, а конец – на точку приложения. Векторы широко используются в физике, математике, геометрии и других науках.
Нулевым вектором называется такой вектор, у которого длина равна нулю. Он не имеет направления и не указывает на точку приложения. Нулевой вектор обозначается символом 0 или O, и он является особенным вектором, так как он никак не изменяется при сложении или вычитании других векторов.
Для наглядного понимания можно представить, что нулевой вектор – это пустая стрелка, которая не имеет ни начала, ни конца. Он не обладает никакими характеристиками, кроме своей длины, равной нолю.
Вектор и его определение
В физике и математике вектором называется направленный отрезок, который характеризуется своей длиной и направлением.
Длина вектора (модуль) представляет собой значение физической величины, которую он представляет. Направление вектора задается прямой, на которой лежит вектор. Стартовая точка вектора называется его началом, а конечная точка – концом.
Нулевой вектор – это вектор, у которого длина равна нулю. Все его компоненты также равны нулю. Другими словами, нулевой вектор не имеет направления и представляет собой точку в пространстве. Он не может быть описан как «вправо» или «вверх», так как у него нет длины и направления.
Компоненты вектора
Вектор может быть представлен в виде набора компонентов, которые указывают на изменение величины по каждой из осей координатной системы. Например, двумерный вектор имеет две компоненты – горизонтальную и вертикальную.
Операции с векторами
Векторы можно складывать, вычитать и умножать на число. При сложении или вычитании векторов, их компоненты складываются или вычитаются по отдельности. Умножение вектора на число приводит к умножению каждой компоненты вектора на это число. Также можно выполнять операции скалярного и векторного произведения векторов.
Векторы широко применяются в физике и математике для решения различных задач. Они позволяют описывать движение, силы, совершать геометрические преобразования и многое другое.
| Операция | Обозначение | Формула |
|---|---|---|
| Сложение | a + b | ci = ai + bi (для каждой компоненты) |
| Вычитание | a — b | ci = ai — bi (для каждой компоненты) |
| Умножение на число | α · a | ci = α · ai (для каждой компоненты) |
| Векторное произведение | a × b | … |
| Скалярное произведение | a · b | … |
Итак, вектор – это объект, характеризующийся своей длиной и направлением. Нулевой вектор не имеет длины и направления. Компоненты вектора позволяют описывать изменение величины по каждой из осей. Векторы могут складываться, вычитаться, умножаться на число и иметь скалярное или векторное произведение.
Основные понятия и свойства вектора
Нулевой вектор — это вектор, который не имеет ни направления, ни длины. Он обозначается символом 0 или O. Нулевой вектор начинается и заканчивается в одной точке. Однако, поскольку его длина равна нулю, нулевой вектор влияет только на его направление, а не на физическое перемещение. Можно сказать, что нулевой вектор не имеет смысла в плоском или пространственном представлении и используется только в математических операциях.
Векторы в математике можно складывать по определенным правилам. Сумма двух векторов получается путем сложения их соответствующих компонентов. Также можно умножать вектор на скаляр, это приводит к изменению длины вектора, но не его направления.
Основные свойства вектора:
| Свойство | Описание |
|---|---|
| Коммутативность | Сумма двух векторов не зависит от порядка слагаемых. |
| Ассоциативность | Сумма трех и более векторов не зависит от порядка слагаемых. |
| Дистрибутивность | Умножение вектора на скаляр и сложение его компонент равносильно сложению двух векторов, умноженных на этот скаляр. |
| Существование обратного вектора | Для каждого вектора существует вектор с обратным направлением и противоположной длиной, который при сложении с ним дает нулевой вектор. |
Классификация векторов
- Нулевой вектор: нулевой вектор — это вектор, у которого длина равна нулю. Он не имеет направления и обозначается символом «0». Нулевой вектор играет важную роль в математике, так как является идентификатором для операций над векторами.
- Прямой вектор: прямой вектор — это вектор, у которого направление параллельно заданной линии. Такой вектор может быть положительно направленным (вдоль прямой) или отрицательно направленным (против прямой).
- Единичный вектор: единичный вектор — это вектор, длина которого равна единице. Он используется для указания направления других векторов и обозначается символом «i».
- Коллинеарные и компланарные векторы: коллинеарные векторы — это векторы, которые лежат на одной прямой и имеют одно и то же направление или противоположное направление. Компланарные векторы — это векторы, которые лежат в одной плоскости.
- Ортогональные векторы: ортогональные векторы — это векторы, которые перпендикулярны друг другу. Угол между ортогональными векторами равен 90 градусам.
Это лишь некоторые примеры классификации векторов. Векторы играют важную роль в математике, физике и других науках, и их свойства широко используются в различных приложениях.
Что такое нулевой вектор?
Нулевой вектор обозначается символом «0«. Он не имеет точки приложения и его начало совпадает с концом. Нулевой вектор может быть представлен в виде списка чисел с нулевыми значениеми, например, (0, 0, 0).
Нулевой вектор имеет ряд особенностей. Он является нейтральным элементом для операции сложения векторов, так как при сложении с нулевым вектором другой вектор не изменяется. Также, нулевой вектор является базисным элементом в пространстве векторов и является нулевым вектором любой размерности или направления.
Понимание нулевого вектора важно в различных областях, таких как физика, математика, компьютерная графика и многие другие. Нулевой вектор помогает создавать базисные системы, определять направления и выражать нулевое или отсутствующее значение в различных контекстах.
Свойства нулевого вектора
Существует несколько свойств, которые характеризуют нулевой вектор:
1. Сложение нулевого вектора
Любой вектор, который складывается с нулевым вектором, остается неизменным. Если вектор a — произвольный вектор, а 0 — нулевой вектор, то выполняется равенство a + 0 = a.
2. Умножение нулевого вектора на число
Умножение нулевого вектора на любое число всегда дает нулевой вектор. Если a — нулевой вектор, а k — произвольное число, то выполняется равенство k * a = 0.
Нулевой вектор является особенным вектором, он не имеет направления и не может быть использован для вычислений векторного произведения или определения угла между векторами. Однако, он играет важную роль в линейной алгебре и используется для определения базиса в векторном пространстве.
Равенство и сумма векторов
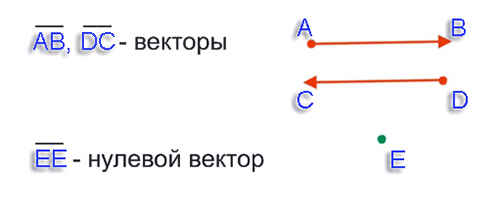
Векторы могут быть равными, если у них одинаковая длина и направление. Если два вектора имеют одинаковую длину и направление, то они считаются равными и обозначаются символом «=». Например, если вектор AB и вектор CD имеют одинаковую длину и направление, то можно записать AB = CD.
Сумма векторов — это операция, которая соединяет два вектора в один вектор. Сумма векторов обозначается символом «+». Чтобы сложить два вектора, их начала должны совпадать, а концы векторов соединяются.
Сумма векторов можно представить с помощью таблицы. В первом столбце таблицы указываются компоненты первого вектора, во втором столбце — компоненты второго вектора, а в третьем столбце — компоненты суммы векторов. Если векторы имеют одинаковое количество компонент, то их можно поэлементно сложить. Например, вектор A = (1, 2) и вектор B = (3, 4). Сумма векторов A и B будет равна вектору C = (4, 6).
| Вектор A | Вектор B | Сумма векторов |
|---|---|---|
| (1, 2) | (3, 4) | (4, 6) |
Нулевой вектор — это вектор, у которого длина равна нулю. Нулевой вектор обозначается символом «0» или «O». Нулевой вектор не имеет направления и не может быть использован для переноса точек в пространстве.
Умножение вектора на число
Для выполнения умножения вектора на число достаточно умножить каждую координату вектора на это число. Таким образом, если у нас есть вектор v со значениями (v1, v2, …, vn) и число a, то умножение вектора на число представляется следующим образом:
| Исходный вектор | Число | Результат умножения |
|---|---|---|
| (v1, v2, …, vn) | a | (a * v1, a * v2, …, a * vn) |
Таким образом, результатом умножения вектора на число будет новый вектор, в котором каждая координата умножена на число. Умножение вектора на число позволяет изменять его длину и направление. Если число положительное, вектор увеличится в размере, если число отрицательное, вектор изменит направление и его длина также будет увеличена.
Умножение вектора на число широко используется во многих областях науки и инженерии, включая физику, компьютерную графику, механику и другие. Оно помогает моделировать и анализировать различные физические явления, а также применяется для решения различных задач, связанных с векторами.
Применение векторов в математике и физике
Математика
Векторы широко применяются в математике, особенно в аналитической геометрии и линейной алгебре. Они позволяют описывать и решать самые разные задачи. Например:
- Определение различных типов пространственных фигур, таких как отрезок, прямая, плоскость.
- Описание смещения или перемещения точки, прямой или плоскости.
- Вычисление суммы или разности векторов.
- Умножение вектора на скаляр.
Физика

Физика как наука, изучающая законы природы, также широко использует векторы для описания физических величин. Некоторые примеры применения векторов в физике:
- Описание силы, действующей на тело.
- Расчет ускорения тела при действии силы.
- Движение тел в трехмерном пространстве.
- Описание магнитных и электрических полей.
- Моделирование траектории движения частицы в электромагнитном поле.
Изучение векторов позволяет более точно описывать и анализировать различные физические явления, делая их более предсказуемыми и управляемыми.
Вопрос-ответ:
Что такое вектор?
Вектор — это математический объект, который имеет определенную длину (модуль) и направление. Векторы используются для описания физических величин, таких как сила, скорость, ускорение и т.д. Вектор обычно обозначается стрелкой над буквой, например, A.
Как определить, что вектор является нулевым?
Вектор называется нулевым, если его длина (модуль) равна нулю. Нулевой вектор обычно обозначается символом 0 или O.
Какие свойства имеют векторы?
Векторы обладают рядом свойств. Например, векторы можно складывать и вычитать, умножать на число и брать скалярное произведение. Они также могут быть перемещены в пространстве без изменения своих характеристик.
Как рассчитать длину вектора?
Длина вектора может быть рассчитана по формуле модуля. Если вектор задан координатами (x, y, z), то его длина будет равна квадратному корню из суммы квадратов этих координат: |A| = √(x² + y² + z²).
Как можно представить вектор графически?
Вектор может быть представлен графически с помощью направленной отрезка прямой линии. Начало и конец отрезка соответствуют начальной и конечной точкам вектора, а направление отрезка указывает на направление вектора.
Что такое вектор?
Вектором называется величина, которая имеет и направление, и величину. Он обозначается стрелкой и характеризуется длиной и направлением.