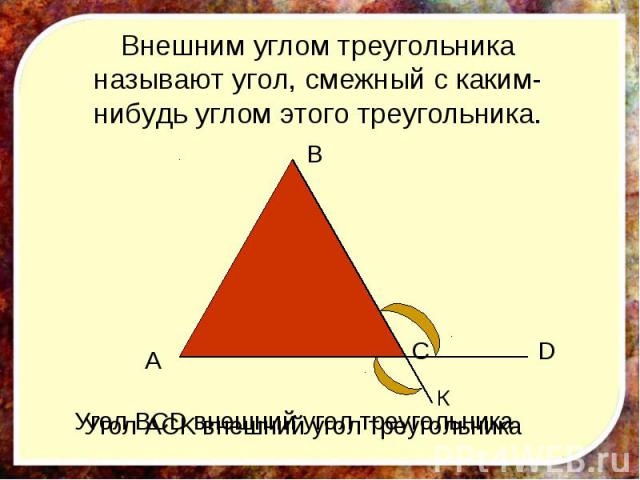
Внешний угол треугольника — это угол, образованный продолжением одной из его сторон и продолжением смежной стороны. Он находится снаружи треугольника.
Чтобы лучше понять, что такое внешний угол треугольника, давайте представим себе треугольник с вершинами A, B и C. Пусть сторона BC продолжена за точку C и пересечется с продолжением стороны AB в точке D. Тогда угол ADC является внешним углом треугольника ABC.
Свойства внешних углов треугольника:
- Сумма всех внешних углов треугольника равна 360 градусам. Это означает, что если мы измерим все внешние углы треугольника и сложим их, получим сумму, равную 360 градусам.
- Внешний угол треугольника всегда больше любого его внутреннего угла. Это свойство легко доказывается с помощью неравенства треугольника.
- Внешний угол треугольника и его смежные внутренние углы образуют линейную пару. Это означает, что сумма внешнего угла и смежного внутреннего угла равна 180 градусам.
Изучение свойств и характеристик внешних углов треугольника помогает нам лучше понять структуру и геометрические отношения внутри треугольника. Это знание может быть полезным при решении различных геометрических задач и задач по тригонометрии.
Определение внешнего угла треугольника

Внешним углом треугольника называется угол, образованный одной стороной треугольника и продолжением этой стороны за его остальные две стороны.
Для правильного определения внешнего угла треугольника необходимо следить за тем, чтобы его вершина находилась за пределами треугольника. Внешний угол может быть направлен как внутрь, так и наружу треугольника.
Внешний угол треугольника имеет важное значение при решении различных задач геометрии. Например, внешние углы треугольника равны сумме соответствующих внутренних углов.
Определение внешнего угла треугольника является важным базовым понятием геометрии и широко используется в различных расчетах и доказательствах свойств треугольников.
| Тип треугольника | Описание |
|---|---|
| Равносторонний треугольник | Внешние углы равны 120 градусов |
| Равнобедренный треугольник | Внешний угол равен сумме внутренних углов |
| Прямоугольный треугольник | Сумма внешних углов равна 360 градусов |
Что такое внешний угол треугольника?
В треугольнике у каждого его угла есть свой внешний угол. Он всегда расположен снаружи треугольника и является смежным к этому углу. В комплект он входит вместе с этим углом и прилежащей к нему стороной.
Сумма всех внешних углов треугольника равна 360 градусов.
Внешние углы треугольника имеют больше полезных свойств и применений. Например, сумма внутренних и внешних углов прилегающих смежных треугольников всегда будет равна 180 градусов.
Как найти внешний угол треугольника?
Метод 1: Известные углы треугольника
Если известны два угла треугольника, можно найти внешний угол третьего угла как разность 180° и суммы известных углов. Например, если два угла треугольника равны 60° и 80°, то внешний угол третьего угла будет равен 180° — (60° + 80°) = 40°.
Метод 2: Известные стороны треугольника
Если известны длины сторон треугольника, можно использовать теорему косинусов для нахождения угла. Формула для вычисления внешнего угла треугольника выглядит следующим образом:
внешний угол = arccos((a^2 + b^2 — c^2) / (2ab))
где a и b — известные стороны треугольника, c — сторона, примыкающая к внешнему углу.
Применив данный метод, можно найти внешний угол треугольника с известными сторонами.
Найденный внешний угол треугольника может быть полезен при решении различных геометрических задач или в построении треугольника по заданным условиям.
Свойства внешнего угла треугольника
Векторная сумма внутреннего и внешнего углов треугольника равна 180 градусам. Это свойство можно использовать для нахождения неизвестных углов треугольника при известных значениях других углов.
Внешний угол треугольника также является суммой двух внутренних углов, не смежных с ним.
Для любого треугольника сумма внешних углов всегда равна 360 градусов.
Свойства внешнего угла треугольника могут быть использованы в различных геометрических задачах, в том числе при решении задач на построение треугольников.
Отличие внешнего угла от внутреннего угла треугольника
В геометрии внешним углом треугольника называется угол, образованный продолжением одной из его сторон и другой стороной треугольника. Отличие внешнего угла от внутреннего угла треугольника заключается в их положении относительно самого треугольника.
Внутренний угол треугольника находится внутри фигуры и образуется двумя его сторонами. Сумма внутренних углов треугольника всегда равна 180 градусов.
Внешний угол треугольника образуется стороной треугольника и продолжением другой его стороны. Внешний угол всегда больше любого из внутренних углов.
Если сложить меры внутреннего и внешнего угла, получится 180 градусов. Например, если внутренний угол треугольника равен 60 градусов, то внешний угол будет равен 120 градусов. Это связано с тем, что внутренний и внешний углы являются смежными и образуют линейную пару.
Отличие внешнего и внутреннего углов треугольника имеет важные последствия при решении геометрических задач. Например, внешние углы треугольника равны сумме противоположных внутренних углов. Это свойство позволяет решать разнообразные задачи, связанные с построением и вычислением углов треугольника.
Практическое применение внешнего угла треугольника
Одно из практических применений внешнего угла треугольника встречается в архитектуре. Проектировщики зданий используют внешние углы треугольников, чтобы создать эстетическую красоту и уникальный дизайн зданий. Внешние углы могут использоваться, например, для создания разных форм крыш, окон или декоративных элементов зданий.
Еще одним практическим применением внешнего угла треугольника является определение направления. Ориентирование на местности может осуществляться с помощью треугольников и их внешних углов. Например, если необходимо определить направление движения, можно использовать внешний угол как точку отсчета. Поворот в определенном угле относительно внешнего угла позволяет определить новое направление.
Практическое применение внешнего угла треугольника можно найти и в геодезии. Геодезисты используют треугольники и их внешние углы для измерения искусственных и природных объектов, а также для съемки ландшафта и создания топографических карт. Внешние углы треугольников помогают геодезистам получить более точные и надежные данные для последующей обработки.
И наконец, практическое применение внешнего угла треугольника может быть найдено в тригонометрии и геометрии. Внешние углы треугольников используются для расчетов и измерений, таких как определение длины стороны треугольника или вычисление площади треугольника.
Таким образом, знание и использование внешних углов треугольников играет важную роль в различных сферах практической деятельности, от архитектуры до геодезии и математики. Понимание применения внешнего угла треугольника позволяет решать разнообразные задачи и совершенствовать профессиональные навыки.
Существование внешних углов треугольника
Сумма всех внешних углов треугольника равна 360 градусов. Это свойство позволяет использовать внешние углы треугольника для решения различных задач и задач геометрии.
Внешние углы треугольника также имеют важное геометрическое свойство. Если мы продолжим все три стороны треугольника наружу, то внешние углы будут образовывать линейку, то есть они будут лежать на одной прямой. Это свойство называется линейностью внешних углов треугольника.
Свойства внешних углов треугольника:
- Сумма всех внешних углов треугольника равна 360 градусов.
- Внешние углы треугольника лежат на одной прямой — это свойство называется линейностью внешних углов треугольника.
Знание свойств внешних углов треугольника поможет понять его внутренние углы и сделать более точные геометрические выкладки.
Примеры решения задач на внешний угол треугольника
Рассмотрим несколько примеров задач на внешний угол треугольника:
Пример 1:
Найти меру внешнего угла треугольника, если известны меры двух его внутренних углов.
Решение:
Для начала нужно определить, какой из двух внутренних углов мы считаем внешним. Пусть это будет угол A. Тогда внешний угол, образованный продолжением стороны AB и стороной, соединяющей вершину A с вершиной угла, будет равен сумме мер внутреннего угла B и угла между сторонами AB и BC. Таким образом, мера внешнего угла треугольника равна сумме мер двух внутренних углов.
Пример 2:
Найти меру внутреннего угла треугольника, если известны меры двух его внешних углов.
Решение:
Для начала нужно определить, какой из двух внешних углов мы считаем внутренним. Пусть это будет угол A. Тогда мера внутреннего угла, образованного продолжением стороны AB и стороной, соединяющей вершину A с вершиной угла, будет равна разности мер внешнего угла C и угла между сторонами AB и BC. Таким образом, мера внутреннего угла треугольника равна разности мер двух внешних углов.
Вопрос-ответ:
Что такое внешний угол треугольника?
Внешний угол треугольника — это угол, который образуется продолжением одной из сторон треугольника и перпендикуляром к продолжению другой стороны.
Как посчитать внешний угол треугольника?
Для того чтобы посчитать внешний угол треугольника, нужно найти сумму двух внутренних углов, которые не являются смежными с данным внешним углом.
Каковы свойства внешнего угла треугольника?
Свойства внешнего угла треугольника следующие: 1) сумма всех внешних углов треугольника равна 360 градусов; 2) внешний угол всегда больше любого из внутренних углов данного треугольника.
Зачем нужны внешние углы треугольника?
Внешние углы треугольника используются для решения различных задач и построения фигур. Они могут помочь определить направление движения, найти отражение или поворот вокруг точки.
Могут ли внешние углы треугольника быть отрицательными?
Нет, внешние углы треугольника не могут быть отрицательными. Внешний угол всегда положительный и имеет определенную величину в градусах.
Какой угол в треугольнике называется внешним углом?
Внешним углом треугольника называется угол, который образуется продолжением одной из сторон треугольника со стороной, находящейся внутри треугольника.