Многогранник – это геометрическая фигура, которая образуется путем соединения плоского многоугольника с помощью отрезков или ребер. Такой многогранник может иметь различное количество граней, вершин и ребер, в зависимости от своей формы и сложности.
Основой многогранника является плоский многоугольник, который служит базовой фигурой для построения многогранника. Плоский многоугольник представляет собой фигуру, у которой все вершины лежат в одной плоскости. Он может быть треугольником, квадратом, пятиугольником и т.д., в зависимости от числа его сторон.
К плоскому многоугольнику в многограннике добавляются точки и отрезки или ребра, которые соединяют вершины многоугольника. Точки и отрезки образуют новые грани и вершины многогранника и придают ему объемную форму.
Многогранник, состоящий из плоского многоугольника, точек и отрезков соединяющих их, является важной геометрической конструкцией. Он может применяться в различных сферах, таких как архитектура, графика, инженерия и другие. Понимание его основных характеристик и свойств позволяет решать задачи по его конструированию и анализу.
Что такое многогранник?
Грани — это плоские фигуры, образованные отрезками, соединяющими вершины многогранника. Грани могут быть треугольными, четырехугольными, пятиугольными и так далее, в зависимости от формы плоского многоугольника.
Вершины — это точки, в которых пересекаются ребра многогранника. Вершины многогранника могут быть трехмерными, то есть находиться в разных плоскостях.
Ребра — это отрезки, соединяющие вершины многогранника. Ребра определяют форму многогранника и его структуру.
Многогранники могут быть различных форм и размеров. Некоторые из них — куб, пирамида, призма, тетраэдр и многие другие. Они используются в геометрии, архитектуре, компьютерной графике и других областях для моделирования и изучения трехмерных объектов и пространственных отношений.
Какие многогранники существуют?
Один из самых известных многогранников – это пирамида. Пирамида имеет одну плоскую грань в форме многоугольника, называемого основанием, и треугольные грани, соединяющие вершины основания с одной общей вершиной – вершиной пирамиды. Пирамида может быть треугольной, четырехугольной, пятиугольной и т.д., в зависимости от формы основания.
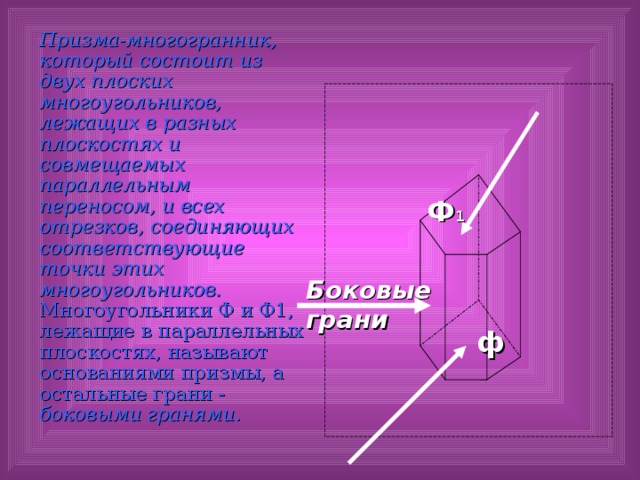
Другой тип многогранников – это призма. Призма также имеет две плоские грани в форме многоугольников, называемых основаниями, и прямоугольные (или косоугольные) грани, соединяющие соответствующие вершины оснований. Призмы могут быть треугольными, четырехугольными, пятиугольными и т.д.
Остальные многогранники бывают более сложными и имеют больше граней. К ним относятся такие многогранники, как параллелепипеды, икосаэдры, додекаэдры, октаэдры и т.д. Эти многогранники имеют разные формы граней, но все они состоят из плоского многоугольника и отрезков, соединяющих его вершины.
Многогранники являются важными объектами в геометрии и имеют различные применения в науке и технике. Изучение и классификация многогранников помогает углубить понимание их свойств, а также применять их в практических задачах.
Правильные многогранники
Примерами правильных многогранников являются такие известные фигуры, как тетраэдр, куб, октаэдр, додекаэдр и икосаэдр. Эти многогранники имеют строго определенное количество граней, ребер и вершин, которое называется числом Фибоначчи.
Правильные многогранники обладают симметрией и регулярностью, что делает их особенно интересными для изучения. Важную роль правильные многогранники играют в математике, физике, химии и других науках, а также в искусстве и дизайне.
Изучение правильных многогранников позволяет лучше понять основные принципы построения трехмерных фигур, а также способы их визуализации и манипулирования. Правильные многогранники являются важным инструментом для моделирования и анализа различных объектов и систем.
Неправильные многогранники
Такие многогранники могут быть очень разнообразными. Например, одним из известных неправильных многогранников является тетраэдр, у которого все грани являются равносторонними треугольниками, но не все ребра и вершины равны.
Особенности неправильных многогранников
Неправильные многогранники обладают несколькими интересными свойствами:
- Имеют различные длины ребер и/или различные углы между гранями;
- Не обладают симметрией относительно центра или плоскостей симметрии;
- Могут иметь различные комбинации треугольников, четырехугольников и других многоугольников в качестве граней;
- Часто встречаются в кристаллических структурах некоторых минералов и соединений.
Примеры неправильных многогранников:
- Октаэдр — имеет 8 граней, которыми являются равносторонние треугольники;
- Икосаэдр — имеет 20 граней, которыми являются равносторонние треугольники;
- Додекаэдр — имеет 12 граней, которыми являются правильные пятиугольники.
Неправильные многогранники являются объектами изучения в геометрии и математике. Они имеют множество интересных свойств и применений в различных областях, таких как химия, физика и информатика.
Как строится многогранник?
Многогранником называется фигура в трехмерном пространстве, состоящая из плоских многоугольников (граней), которые соединены по ребрам.
Построение многогранника начинается с выбора плоского многоугольника, который станет основанием фигуры. Далее, каждая точка основания соединяется отрезком с одной и той же точкой внешней точкой. Эти отрезки называются ребрами многогранника. Кроме того, каждая вершина многогранника соединяется ребром с той вершиной, которая расположена на том же уровне.
В процессе построения многогранника важно правильно выбрать тип основания и определить количество точек на его границе. От этого зависит форма и количество граней фигуры. Например, если основание является треугольником, то многогранник будет состоять из четырех граней (трех сторон треугольника и одной крышки).
Построение многогранника можно визуализировать с помощью таблицы. В верхней строке таблицы записываются точки основания, а в столбцах таблицы указываются соответствующие точки вершин фигуры. Затем проводятся отрезки между точками, чтобы получить ребра многогранника.
Таким образом, построение многогранника включает выбор основания, соединение точек основания с внешними точками, соединение вершин многогранника ребрами и визуализацию через таблицу.
Из каких элементов состоит многогранник?

Многогранник состоит из следующих элементов:
- Плоский многоугольник – основание многогранника. Он может быть треугольником, квадратом, пятиугольником и так далее.
- Вершины – это угловые точки плоского многоугольника, которые связываются отрезками.
- Ребра – отрезки, соединяющие вершины многогранника. Каждому ребру соответствует пара вершин, которые оно соединяет.
- Грани – это плоские фигуры, образованные ребрами между вершинами. Грани многогранника могут быть треугольниками, прямоугольниками, пятиугольниками или другими многоугольниками.
- Углы – это точки пересечения граней многогранника. Углы определяются вершинами и ребрами.
Все эти элементы вместе создают трехмерную фигуру, которая называется многогранником. Количество вершин, ребер, граней и углов может варьироваться в зависимости от формы и размера многогранника.
Как соединяются элементы многогранника?
Многогранник, состоящий из плоского многоугольника, точек и отрезков, имеет специфическую структуру, где каждый элемент взаимосвязан с другими. Соединение элементов многогранника осуществляется с помощью отрезков.
Отрезки могут соединять вершины многогранника, создавая его грани. Грани представляют собой плоские многоугольники, которые ограничивают внутреннее пространство многогранника и делят его на различные части — грани. Каждая грань имеет свое название, которое определяется геометрическими свойствами и расположением вершин и отрезков.
Кроме того, отрезки могут соединять вершины с ребрами многогранника, а также ребра с другими ребрами. Ребра представляют собой отрезки, которые соединяют две вершины и определяют границы многогранника.
Важно отметить, что соединение элементов многогранника должно быть правильным и соответствовать его геометрическим свойствам. Неправильное соединение может привести к деформации или изменению формы многогранника, что может оказать влияние на его свойства и функциональность.
Примеры из реальной жизни
1. Упаковка и хранение товаров: Многогранники используются для оптимальной упаковки и хранения различных товаров. Коробки, ящики и контейнеры часто имеют форму многогранников, чтобы удобно помещаться в друг друга и использовать пространство максимально эффективно.
2. Архитектура и дизайн: Многогранники часто встречаются в архитектуре и дизайне. Геометрические формы, такие как пирамиды, призмы и кубы, часто используются для создания интересных и эстетически привлекательных строений и объектов.
3. Телекоммуникации: Многогранники играют важную роль в телекоммуникационных системах, особенно при передаче сигналов. Например, в сотовых сетях используются многогранники для разделения сот и определения зон покрытия.
4. Кристаллы и минералы: Многогранники часто наблюдаются в кристаллах и минералах. Например, бриллианты имеют форму ромбической призмы, кварц имеет форму шестиугольной призмы, а соли часто образуют кубическую сетку.
5. Игры и головоломки: Многогранники используются в различных играх и головоломках. Например, Рубикова кубика состоит из множества маленьких кубиков, которые могут быть повернуты для достижения определенной конфигурации. Также существуют различные головоломки основанные на пирамидах, призмах и других многогранниках.
Многогранники представляют собой замечательный и универсальный инструмент для моделирования и понимания множества явлений в реальной жизни. Их геометрические свойства и особенности находят широкое применение в разных областях науки, техники, искусства и дизайна.
Вопрос-ответ:
Что такое многогранник?
Многогранник — это пространственная фигура, состоящая из плоских многоугольников, точек и отрезков, которые их соединяют.
Какие элементы включает в себя многогранник?
Многогранник включает в себя плоские многоугольники, точки и отрезки, которые служат соединением между ними.
Каким образом строится многогранник?
Многогранник строится путем соединения плоских многоугольников, точек и отрезков, чтобы создать пространственную фигуру.
Можно ли сказать, что многогранник — это трехмерная фигура?
Да, многогранник является трехмерной фигурой, так как он существует в трех измерениях.
Чем отличается многогранник от двумерной фигуры?
Многогранник отличается от двумерной фигуры тем, что он имеет объем и существует в трех измерениях, в то время как двумерная фигура существует только на плоскости.