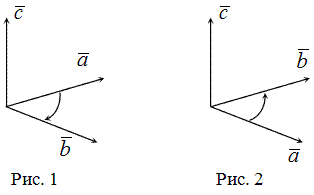
Тройка некомпланарных векторов – это особая конфигурация векторов, которая применяется при изучении различных областей науки и инженерии. Такая тройка векторов является основой для решения множества задач и имеет свои особенности, которые необходимо учитывать.
Некомпланарность означает, что векторы не лежат в одной плоскости, а образуют трехмерную конфигурацию. При этом тройка векторов может быть правой или левой. Если тройка векторов является правой, то существует такой порядок векторов, при котором векторное произведение первых двух векторов будет направлено по направлению третьего вектора. Такая конфигурация является частным случаем и имеет особое значение при решении задач.
Правая конфигурация тройки некомпланарных векторов находит применение во многих областях. Например, в механике правая тройка используется для определения направления вращения твердого тела. В электромагнетизме правая тройка может использоваться для определения магнитного поля, созданного электрическим током. В физике также широко используется понятие правой тройки векторов для описания различных физических явлений.
Знание о тройке некомпланарных векторов в правой конфигурации является важным фундаментом для понимания и решения задач, связанных с трехмерной геометрией и векторным анализом. Правильное понимание особенностей такой конфигурации векторов позволяет более точно и эффективно решать множество задач, возникающих в научной и инженерной практике.
Определение тройки некомпланарных векторов
Для определения некомпланарности тройки векторов используется правило правой руки. Если пальцы руки расположены вдоль первого вектора и можно из него перейти ко второму вектору, проводя пальцами некоторое направление, считается, что тройка векторов образует правую конфигурацию и является некомпланарной.
Если же переход от первого вектора ко второму происходит в противоположном направлении, то тройка векторов образует левую конфигурацию и является компланарной, то есть лежит в одной плоскости.
Определение тройки некомпланарных векторов имеет важное значение в геометрии, физике и других науках, где трехмерное пространство используется для описания и решения задач.
Линейная независимость
Если тройка векторов заполняет пространство, то она называется базисом этого пространства. Для трехмерного пространства требуется, чтобы три вектора были линейно независимыми и некомпланарными.
Линейная независимость является одним из основных понятий в линейной алгебре и имеет важное значение при решении систем линейных уравнений, подсчете размерности пространства и многих других задачах.
Некомпланарность векторов
Некомпланарность векторов может быть проверена при помощи скалярного произведения. Для того чтобы векторы были компланарными, их скалярное произведение должно быть равно нулю. Если же скалярное произведение отлично от нуля, то векторы некомпланарны и образуют тройку некомпланарных векторов.
Важно отметить, что некомпланарные векторы могут образовывать различные конфигурации. Одной из таких конфигураций является правая конфигурация тройки некомпланарных векторов. Правая конфигурация означает, что векторы могут быть представлены в виде правой тройки координат или что их векторное произведение положительно.
Таким образом, некомпланарность векторов является важной характеристикой, определяющей их расположение в пространстве. Знание о тройке некомпланарных векторов и их конфигурации может быть полезным при решении задач в различных научных и инженерных областях.
| Признак некомпланарности | Скалярное произведение | Векторное произведение |
|---|---|---|
| Компланарные векторы | 0 | 0 |
| Некомпланарные векторы | Не равно 0 | Не равно 0 |
Правая конфигурация
Такая конфигурация тройки векторов часто встречается в физике и математике, и она играет важную роль в многих областях науки. Например, векторное произведение двух векторов определяется с помощью правой конфигурации: результатом их векторного произведения является вектор, направление которого задается с использованием правой руки.
Правая конфигурация также важна при работе с координатами и ориентацией в трехмерном пространстве. Направление осей координат в таком пространстве определяется с помощью правой конфигурации, что позволяет удобно и естественно описывать положение объектов и учитывать их взаимодействие.
Свойства тройки некомпланарных векторов
Тройка векторов считается некомпланарной, если они не лежат в одной плоскости. Это означает, что ни один вектор из тройки не может быть выражен в виде линейной комбинации двух других векторов.
Свойства тройки некомпланарных векторов:
| 1. | Некомпланарные векторы образуют систему векторов, которая не может быть сведена к меньшему числу векторов. Если из тройки векторов можно отбросить один и оставшиеся два вектора будут компланарными, то тройка называется компланарной. |
| 2. | Некомпланарные векторы могут использоваться для описания трехмерных объектов, так как позволяют задавать направление и величину векторных величин в трехмерном пространстве. |
| 3. | Если тройка некомпланарных векторов задает систему координат в трехмерном пространстве, то любая точка в этом пространстве уникально определяется значениями трех компонент векторов. |
| 4. | Тройка некомпланарных векторов обладает независимостью компонент. Это означает, что изменение значения одной компоненты вектора не приведет к изменению значений остальных компонент. |
Коммутативность и ассоциативность
Так, для трех векторов a, b и c выполняется равенство:
a × b = — b × a
а также равенство:
a ∙ b = b ∙ a
Это свойство позволяет менять порядок векторов в операциях без влияния на результат.
Ассоциативность означает, что при выполнении операции с несколькими векторами результат не зависит от того, в каком порядке выполняются операции. Для трех векторов a, b и c выполняется равенство:
(a × b) × c = a × (b × c)
В результате, при изменении порядка операций произведения векторов, результат останется неизменным.
Скалярное произведение
Для тройки некомпланарных векторов, скалярное произведение определяется следующим образом:
- Рассмотрим векторное произведение первых двух векторов и обозначим его как вектор А:
- Вычислим скалярное произведение вектора А и третьего вектора V3:
А = А1xА2
P = А·V3
Если векторное произведение и скалярное произведение имеют одинаковые знаки, то тройка векторов считается правой, иначе – левой. Правая конфигурация векторов означает, что они образуют правую тройку в пространстве.
Скалярное произведение векторов имеет следующие свойства:
- Коммутативность:
А·B = B·A - Дистрибутивность по сложению:
(А + B)·C = А·C + B·C - Ассоциативность умножения на скаляр:
(kA)·B = k(A·B) - Независимость от выбора базиса:
А·B = 0, если А = 0 или B = 0
Скалярное произведение векторов широко применяется в различных областях науки и техники, таких как физика, геометрия, компьютерная графика и многих других.
Вопрос-ответ:
Что такое тройка некомпланарных векторов?
Тройка некомпланарных векторов — это тройка векторов, которые не лежат на одной плоскости и не могут быть выражены как линейная комбинация друг друга.
В чем заключается правая конфигурация тройки некомпланарных векторов?
Правая конфигурация тройки некомпланарных векторов означает, что если смотреть в направлении первого вектора, то векторное произведение второго и третьего векторов будет направлено в положительном направлении оси, совпадающей с направлением первого вектора.
Как определить, является ли тройка векторов тройкой некомпланарных векторов?
Чтобы определить, является ли тройка векторов тройкой некомпланарных векторов, необходимо вычислить их смешанное произведение. Если смешанное произведение не равно нулю, то тройка векторов некомпланарна.
Как проверить, что тройка некомпланарных векторов образует правую конфигурацию?
Для проверки правой конфигурации тройки некомпланарных векторов нужно вычислить их векторное произведение. Если результат векторного произведения имеет положительную знаковую ориентацию, то тройка образует правую конфигурацию.
Каким образом правая конфигурация тройки некомпланарных векторов может быть применена в практических ситуациях?
Правая конфигурация тройки некомпланарных векторов может быть применена, например, в физике при определении направления вращения колеса автомобиля или в инженерии при проектировании механизмов, где необходимо знать направление вращения.