В физике и математике проекция вектора перемещения – это величина, которая показывает, какая часть вектора приходится на определенную ось. Проекция вектора на координатную ось определяется с помощью трехмерных или двухмерных координат и используется для анализа движения тела в пространстве.
Для определения проекции вектора перемещения на координатную ось необходимо произвести скалярное произведение данного вектора и единичного вектора, который соответствует оси. При этом результатом будет величина, показывающая, какая часть вектора приходится на данную координатную ось.
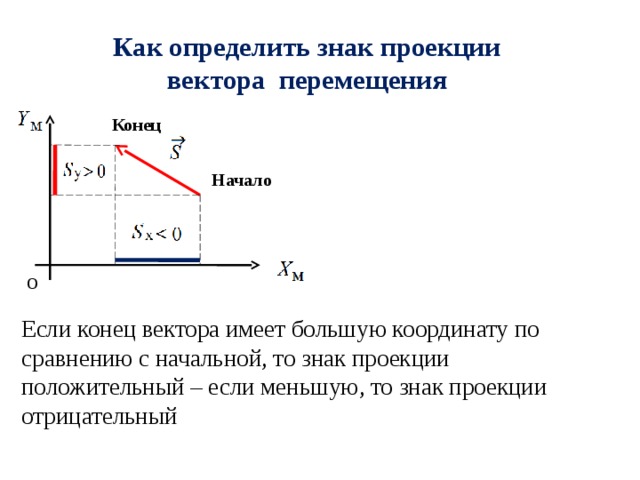
Проекция вектора перемещения на координатную ось может быть положительной или отрицательной в зависимости от направления вектора и оси. Если проекция положительна, значит вектор направлен в положительном направлении оси, а если отрицательна – то вектор направлен в отрицательном направлении оси.
Определение проекции вектора перемещения
Для определения проекции вектора перемещения на координатную ось необходимо выполнить следующие шаги:
- Разложить вектор перемещения на компоненты, параллельные и перпендикулярные данной оси.
- Найти длину компоненты, параллельной оси. Это и будет являться проекцией вектора перемещения на данную ось.
Проекция вектора перемещения может быть положительной или отрицательной, в зависимости от направления вектора и выбранной оси. Если проекция положительна, значит, вектор перемещения направлен в положительном направлении оси, если отрицательна — вектор перемещения направлен в отрицательном направлении оси.
Определение проекции вектора перемещения позволяет анализировать движение объектов в пространстве и изучать их перемещение по отдельным координатным осям. Это важное понятие в физике, инженерии и многих других областях, где требуется анализ векторного перемещения.
Понятие проекции вектора
Чтобы вычислить проекцию вектора на координатную ось, нужно проектировать вектор на ось, используя формулу проекции. Для проекции вектора на ось X, берется скалярное произведение данного вектора на единичный вектор, параллельный оси X. Аналогично, для проекции вектора на ось Y, используется скалярное произведение вектора на единичный вектор, параллельный оси Y.
Проекция вектора может быть положительной или отрицательной, в зависимости от того, на какую сторону оси она смотрит. Положительная проекция указывает на то, что тень вектора направлена в положительном направлении оси, а отрицательная проекция указывает на направление в отрицательном направлении оси.
Знание проекции вектора на координатную ось может быть полезно для определения его компонентов на этой оси. Проекции на оси X и Y в сумме дают исходный вектор, то есть проекция на каждую из осей дает информацию о свойствах вектора на этой оси.
Значение проекции вектора
Проекция вектора перемещения на координатную ось представляет собой проекцию вектора на эту ось. Она позволяет определить, насколько смещается объект вдоль данной оси.
Значение проекции вектора является величиной, которая показывает, какое расстояние перемещается объект по выбранной оси. Она обычно измеряется в единицах, соответствующих этой оси (например, в метрах, если ось представляет собой измерение длины).
Для определения значения проекции вектора перемещения на координатную ось нужно умножить длину вектора на косинус угла между вектором и данной осью.
Значение проекции вектора можно использовать для решения различных задач, связанных с перемещением объектов. Например, оно может помочь определить, насколько далеко объект перемещается по горизонтальной оси или вертикальной оси.
Определение проекции вектора перемещения
Для определения проекции вектора перемещения на координатную ось необходимо использовать скалярное произведение вектора перемещения и единичного вектора, направленного вдоль оси. Скалярное произведение позволяет найти проекцию вектора на выбранную ось, учитывая его направление и длину.
Формула для определения проекции вектора перемещения выглядит следующим образом:
Проекция = (Вектор перемещения * Единичный вектор) * Единичный вектор
Где Вектор перемещения — вектор, описывающий перемещение объекта, а Единичный вектор — единичный вектор, параллельный выбранной оси.
Определение проекции вектора перемещения является важным инструментом в физике и математике, так как позволяет анализировать движение объектов в пространстве и измерять перемещение вдоль определенной оси.
Как определить проекцию вектора перемещения
Для нахождения проекции вектора перемещения на ось X используется формула: Px = |D| * cos α, где |D| — длина вектора перемещения, а α — угол между вектором и осью X.
Аналогично, для нахождения проекции вектора перемещения на ось Y используется формула: Py = |D| * sin α.
Таким образом, для определения проекции вектора перемещения на каждую из координатных осей, необходимо знать длину вектора перемещения и угол между вектором и соответствующей осью.
Шаг 1: Найти коэффициент угла между вектором перемещения и координатной осью
Проекция вектора перемещения на координатную ось представляет собой компонент вектора, который лежит вдоль этой оси. Для определения проекции на одну из осей необходимо найти коэффициент угла между вектором перемещения и этой осью.
Для начала определим угол между вектором перемещения и осью, использующую следующую формулу:
Шаг 2: Умножить длину вектора перемещения на косинус угла между вектором перемещения и координатной осью
Для этого мы умножаем длину вектора перемещения на косинус угла между вектором перемещения и координатной осью. Косинус угла можно найти с помощью геометрических выкладок или с использованием тригонометрических функций (например, cos(angle)).
Таким образом, проекция вектора перемещения на определенную координатную ось равна произведению длины вектора перемещения на косинус угла между вектором перемещения и этой координатной осью.
Этот подход позволяет нам определить величину компоненты вектора перемещения вдоль конкретной координатной оси. Зная все проекции на различные оси, мы можем полностью описать вектор перемещения.
Вопрос-ответ:
Что такое проекция вектора перемещения на координатную ось?
Проекция вектора перемещения на координатную ось — это проекция данного вектора на соответствующую ось координатной системы (направление оси определяется положительным направлением).
Как определить проекцию вектора перемещения на координатную ось?
Для определения проекции вектора перемещения на координатную ось необходимо найти скалярное произведение этого вектора на единичный вектор, направленный вдоль оси. Результатом будет длина проекции вектора перемещения.
Что такое проекция вектора перемещения?
Проекция вектора перемещения на координатную ось представляет собой длину этой проекции, которая является числовым значением и показывает, насколько вектор перемещения направлен вдоль выбранной оси. Проекция может быть положительной, если вектор направлен в положительном направлении оси, отрицательной, если вектор направлен в отрицательном направлении оси, или равной нулю, если вектор перпендикулярен оси.
Для чего нужно определять проекцию вектора перемещения на координатную ось?
Определение проекции вектора перемещения на координатную ось является важной операцией в физике и математике. Она позволяет вычислить, насколько вектор перемещения направлен вдоль данной оси, что может быть полезно при решении задач, связанных с движением тела по прямой линии или в пространстве. Кроме того, проекция может быть использована для определения компонентов вектора по разным осям, что упрощает анализ векторных данных.