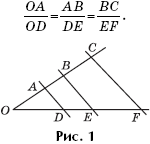
Пропорциональные отрезки – это такие отрезки, длины которых имеют определенное отношение друг к другу. Они часто встречаются в геометрии и математике, а также широко используются в других науках и повседневной жизни. Знание о пропорциональных отрезках позволяет решать множество задач, связанных с расчетами и измерениями.
Чтобы определить, являются ли отрезки пропорциональными, необходимо проверить, соблюдаются ли условия пропорции. Пропорция представляет собой равенство двух отношений. В случае с отрезками, мы сравниваем их длины. Если отношение длин одних отрезков к длинам других отрезков одинаково, то они являются пропорциональными. Например, если отрезок AB относится к отрезку CD так же, как отрезок EF относится к отрезку GH, то мы можем записать это в виде пропорции AB/CD = EF/GH.
Пропорциональные отрезки имеют ряд важных свойств. Одно из них – свойство расположения точек на отрезках. Если две точки делят отрезок на три равные части, то они делят другой отрезок на три равные части в том же отношении. Это свойство также применимо к другим отношениям длин пропорциональных отрезков.
Основные понятия пропорциональности
Для определения пропорциональности отрезков необходимо выполнение следующего условия: если отношение длин двух отрезков равно отношению длин двух других отрезков, то эти отрезки называются пропорциональными. Таким образом, пропорциональные отрезки имеют одинаковое или равное отношение длин.
Пропорции могут быть представлены в виде таблицы, где столбцы обозначают длины отрезков, а строки — соответствующие отношения длин. Стандартная форма представления пропорции — это таблица с четырьмя столбцами. В первом и втором столбцах записываются длины отрезков, а в третьем и четвертом столбцах — соответствующие отношения длин.
| Отрезок AB | Отрезок CD | Отношение AB к CD | Отношение CD к AB |
|---|---|---|---|
| AB | CD | AB/CD | CD/AB |
Пропорции могут использоваться для решения различных математических проблем, включая нахождение неизвестных длин отрезков или проверку соотношений между отрезками. Пропорциональные отрезки также применяются в геометрии, физике и других областях, где необходимо сравнить или определить соотношение разных величин.
Пропорциональность в математике
Математически пропорциональность выражается через равенство отношений между двумя параллельными прямыми. Если обозначить первое отношение как a:b и второе отношение как c:d, то пропорция будет записываться как a:b = c:d.
Отношение пропорциональности можно наглядно представить с помощью таблицы:
| Первая величина | Вторая величина |
|---|---|
| a | c |
| b | d |
Такая таблица говорит о том, что отношение a:b равно отношению c:d и числа a, b, c и d пропорциональны друг другу.
Пропорциональность позволяет решать множество задач и применяется в различных областях знания, например, в физике, экономике и геометрии. Понимание пропорциональности поможет в уяснении многих математических концепций и способствует развитию логического мышления.
Пропорциональность в геометрии
Два отрезка называются пропорциональными, если их отношение равно отношению их длин. Другими словами, если мы имеем два отрезка AB и CD, то они будут пропорциональными, если отношение длины отрезка AB к длине отрезка CD будет равно отношению их длин.
Мы можем выразить пропорциональность математически. Если AB и CD пропорциональны, то мы можем записать это следующим образом: AB/CD = AC/BD, где AC и BD — другие отрезки, параллельные AB и CD.
Приведенная формула позволяет нам находить значение неизвестных отрезков в пропорциональных отношениях. Если, например, мы знаем длину отрезка AB и отношение его длины к длине отрезка CD, мы можем найти длину отрезка CD, используя формулу: CD = AB * BD / AC. Таким образом, пропорциональность помогает нам определить значение неизвестных отрезков.
Таким образом, пропорциональность в геометрии является мощным инструментом для анализа и решения задач. Она позволяет нам определить отношения между различными геометрическими объектами и делает геометрию более понятной и доступной.
Способы определения пропорциональных отрезков
1. Сравнение длин отрезков: Для определения пропорциональности можно сравнить длины двух отрезков. Если отношение их длин остается постоянным, то эти отрезки являются пропорциональными.
2. Использование геометрической пропорции: Пропорция — это равенство двух рациональных отношений. Для определения пропорциональности отрезков можно использовать формулу геометрической пропорции: если отношение длин одного отрезка к длине другого равно отношению длин третьего отрезка к длине четвертого, то эти отрезки пропорциональны.
3. Использование доли: Пропорция может быть определена путем сравнения долей, которые занимают отрезки на оси координат. Если отношение доли первого отрезка к доле второго отрезка равно отношению доли третьего отрезка к доле четвертого, то эти отрезки пропорциональны.
4. Использование подобных фигур: Для определения пропорциональности отрезков можно рассмотреть подобные фигуры, в которых эти отрезки являются сторонами. Если отношение сторон этих фигур одинаково, то отрезки пропорциональны.
Таким образом, для определения пропорциональности отрезков можно использовать различные методы, включающие сравнение длин, использование геометрической пропорции, сравнение долей и рассмотрение подобных фигур.
Метод подобия треугольников
Для определения пропорциональных отрезков с помощью метода подобия треугольников необходимо иметь два треугольника, в которых известны соответствующие стороны. Затем с помощью угловой пропорции можно определить, являются ли треугольники подобными. Если треугольники подобны, то отношения длин сторон будут равны.
Пример:
| Треугольник ABC | Треугольник XYZ |
|---|---|
| AB = 4 см | XY = 8 см |
| BC = 6 см | YZ = 12 см |
| AC = ? | XZ = ? |
Для определения длин сторон треугольника ABC с помощью метода подобия треугольников, нужно найти соответствующие стороны треугольника XYZ. Поскольку треугольники подобны, то пропорция сторон будет равна:
AB / XY = BC / YZ = AC / XZ
Подставляем известные значения:
4 / 8 = 6 / 12 = AC / XZ
Решаем уравнение:
AC = (4 * XZ) / 8
Таким образом, с помощью метода подобия треугольников мы определили, что длина стороны AC равна половине длины стороны XZ, то есть AC = XZ / 2.
Используя метод подобия треугольников, можно с легкостью определить пропорциональные отрезки в различных задачах, связанных, например, с построением фигур, вычислением площадей или определением длин отрезков на карте.
Метод сравнения отношений длин отрезков и их частей
Для определения пропорциональности отрезков, а также их частей, существует метод сравнения отношений. Этот метод основан на принципе, что если два отрезка или их части имеют одинаковое отношение к третьему отрезку или его части, то они пропорциональны.
Для применения данного метода необходимо воспользоваться расчетами отношений длин. Пусть имеются три отрезка A, B и C, и их длины обозначаются соответственно как a, b и c.
Чтобы определить, являются ли отрезки A и B пропорциональными, вычисляют отношения a/b и b/a. Если эти отношения равны, то отрезки A и B пропорциональны.
Если нужно определить, пропорциональны ли отрезки B и C, вычисляют отношения b/c и c/b. Если они равны, то отрезки B и C пропорциональны.
Также возможно сравнить отношения длин частей отрезков. Для этого нужно вычислить отношение между длиной первой части отрезка и длиной второй части, а затем сравнить полученное отношение соответственно для отрезков A и B или B и C.
Применение этого метода позволяет легко определять пропорциональность отрезков и их частей, что важно во многих задачах, связанных с геометрией и арифметикой.
Вопрос-ответ:
Как определить пропорциональные отрезки?
Пропорциональные отрезки определяются по тому, что их отношение постоянно. То есть, если отношение длин двух отрезков всегда остается одинаковым, то такие отрезки являются пропорциональными. Например, отрезки AB и CD являются пропорциональными, если AB/CD = постоянной величине.
Что такое отношение пропорциональных отрезков?
Отношение пропорциональных отрезков – это число, полученное делением длины одного отрезка на длину другого отрезка. Например, если отрезок AB имеет длину 4, а отрезок CD – длину 2, то отношение AB/CD будет равно 2.
Какие свойства имеют пропорциональные отрезки?
Пропорциональные отрезки обладают следующими свойствами: 1) Если AB и CD – пропорциональные отрезки, то AB/CD = постоянная величина; 2) Если AB и CD – пропорциональные отрезки, то CD/AB = обратная величина отношения AB/CD; 3) Если AB и CD – пропорциональные отрезки, то их сумма AC и BD также является пропорциональным отрезком.
Как использовать пропорциональные отрезки в практических задачах?
Пропорциональные отрезки часто используются для нахождения неизвестных значений в задачах, связанных с подобием фигур. Например, если известно, что два треугольника подобны, то соответствующие стороны этих треугольников будут пропорциональными. Используя это свойство, можно находить неизвестные значения.
Как проверить, являются ли отрезки пропорциональными?
Для проверки пропорциональности отрезков нужно сравнить их отношения. Если отношения равны между собой, то отрезки являются пропорциональными. Например, для отрезков AB и CD, чтобы проверить их пропорциональность, нужно вычислить отношение AB/CD и сравнить его с другими отношениями этой же пары отрезков.