Что такое простое число определение и свойства

Простое число – это такое натуральное число, которое имеет ровно два делителя: единицу и само себя. Такое число не делится без остатка ни на какие другие числа, кроме указанных. Простые числа являются одной из фундаментальных концепций математики. Они обладают множеством уникальных и интересных свойств, которые активно изучаются учеными по всему миру.

Одно из первых открытий в области простых чисел было сделано античными греками. Они доказали, что существует бесконечное количество простых чисел. Это означает, что нет самого большого простого числа – они всегда могут быть найдены.

Равномерное распределение простых чисел – это еще одно интересное свойство простых чисел. Если мы возьмем достаточно большое число и случайным образом выберем из него цифры, то вероятность выбрать простое число в результате будет более или менее постоянной. Это означает, что простые числа не скапливаются в определенных диапазонах, а равномерно распределены по числовой прямой.

Содержание

Определение простого числа

Простые числа являются основными строительными блоками для всех остальных чисел. Они обладают рядом уникальных свойств и являются основой множества важных математических концепций и алгоритмов.

Например, любое натуральное число может быть представлено как произведение простых чисел, и это представление называется факторизацией числа. Факторизация чисел имеет широкое применение, например, в криптографии и математическом анализе.

Известно, что бесконечное количество простых чисел, однако их распределение в наборе натуральных чисел неравномерно. Например, простые числа становятся все реже по мере увеличения числа.

Для проверки является ли число простым, можно использовать различные алгоритмы, такие как решето Эратосфена или тест Ферма. Простые числа имеют важное значение в математике и находят своё применение в различных областях.

Простое число в математике

Простые числа играют важную роль в теории чисел и математике в целом. Они являются основными строительными блоками для составления всех остальных натуральных чисел. В самом деле, любое натуральное число можно разложить на простые множители, что называется факторизацией числа.

Несмотря на то, что простые числа представляют собой небольшую долю всех натуральных чисел, они обладают множеством удивительных свойств и особенностей. Например, бесконечность простых чисел была доказана древнегреческим математиком Евклидом более двух тысячелетий назад. С тех пор многие математики изучали их свойства, совершенствуя теорию чисел.

Кроме того, простые числа играют важную роль в различных областях, таких как шифрование и криптография. Например, в алгоритмах шифрования используются большие простые числа для обеспечения безопасности информации.

Простые числа также являются основой для изучения других классов чисел, таких как составные числа, полупростые числа, простые множители и другие.

В таблице ниже приведены некоторые примеры простых чисел:

Число	Делители
2	1, 2
3	1, 3
5	1, 5
7	1, 7
11	1, 11

Как видно из таблицы, простые числа имеют ровно два делителя: единицу и само число. Это отличает их от составных чисел, которые имеют больше двух делителей.

Свойства простого числа

Простые числа имеют несколько свойств:

У простого числа нет делителей, кроме 1 и самого себя. Это означает, что простые числа не могут быть разложены на меньшие множители. Их нельзя представить в виде произведения двух или более чисел, кроме случая, когда один из множителей равен 1.
Простые числа бесконечны. Это утверждение было доказано Евклидом в III веке до н.э. Аргумент Евклида основан на том, что если бы простых чисел было конечное количество, то всегда можно было бы найти еще одно простое число, которое не входит в этот список.
Простые числа имеют много применений в математике и криптографии. Благодаря своим свойствам, простые числа являются основой для многих алгоритмов шифрования, используемых в современных системах безопасности.
Простые числа образуют особую последовательность. Последовательность простых чисел представляет собой непредсказуемую с точки зрения распределения чисел. Существуют законы и теоремы, описывающие и объясняющие некоторые закономерности в расположении простых чисел, но в общем случае позиция каждого нового простого числа в последовательности не может быть предсказана.

Примеры простых чисел

Далее приведены некоторые из самых известных простых чисел:

2 — самое маленькое простое число
3 — второе простое число, которое следует за 2
5 — следующее простое число после 3
7 — после 5 идет это простое число
11 — одно из самых известных простых чисел
13 — следующее после 11 простое число
17 — простое число, которое следует за 13
19 — после 17 идет это простое число
23 — одно из самых известных простых чисел

Приведенные примеры являются лишь небольшой частью множества простых чисел. Всего простых чисел бесконечно много, и их количество неограничено.

Простые числа до 10

Число 2 — это простое число, так как оно делится только на 1 и на само себя.
Число 3 — также является простым числом, поскольку оно делится только на 1 и на 3.
Число 4 делится не только на 1 и на само себя, но еще и на 2. Поэтому 4 не является простым числом.
Число 5 — простое число, так как оно имеет только два делителя: 1 и 5.
Число 6 делится не только на 1 и на само себя, но также на 2 и на 3. Поэтому 6 не является простым числом.
Число 7 — простое число, так как оно имеет только два делителя: 1 и 7.
Число 8 делится не только на 1 и на само себя, но также на 2 и на 4. Поэтому 8 не является простым числом.
Число 9 делится не только на 1 и на само себя, но также на 3. Поэтому 9 не является простым числом.
Число 10 делится не только на 1 и на само себя, но также на 2 и на 5. Поэтому 10 не является простым числом.

Итак, в диапазоне от 1 до 10 есть только два простых числа: 2 и 7.

Простые числа до 100

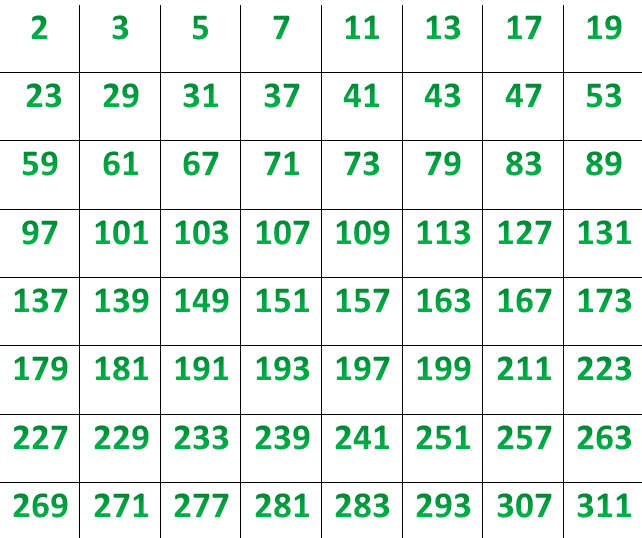
Всего в диапазоне от 1 до 100 существует 25 простых чисел:

Интересно отметить, что простые числа обладают свойством быть неделимыми нацело на любое число, кроме 1 и самого себя. Это свойство делает их важными и полезными в различных применениях, включая шифрование данных и математические алгоритмы.

Помимо простых чисел, все остальные числа можно разложить на простые множители. Таким образом, изучение простых чисел является фундаментальным элементом математики.

Итак, вот все простые числа до 100. Их можно использовать в различных задачах и алгоритмах, требующих простых чисел в данном диапазоне.

Использование простых чисел в криптографии

Одним из ключевых примеров использования простых чисел в криптографии является алгоритм RSA (Rivest-Shamir-Adleman). В основе этого алгоритма лежит факт, что разложение больших чисел на простые множители является очень сложной задачей.

Алгоритм RSA использует два больших простых числа для генерации публичного и приватного ключей. Публичный ключ может быть распространен для шифрования сообщений, в то время как приватный ключ используется для дешифрования зашифрованных сообщений. Обратное разложение числа на простые множители является известной математической проблемой, но является вычислительно сложной.

Комбинация больших простых чисел в алгоритме RSA обеспечивает высокую степень безопасности. Чем больше размерность простых чисел, тем сложнее разложить число на множители и получить приватный ключ.

Но простые числа не используются только для генерации ключей. Они также применяются в других криптографических алгоритмах, таких как диффи-хеллмановский обмен ключами, эллиптические кривые и шифрование блоков.

Таким образом, простые числа играют критическую роль в обеспечении безопасности в криптографии. Изучение и разработка алгоритмов, которые использовали бы простые числа эффективным образом, является важным направлением развития криптографической науки.

Вопрос-ответ:

Что такое простое число?

Простое число — это натуральное число больше 1, которое не имеет других делителей, кроме 1 и самого себя.

Как можно определить простое число?

Чтобы определить, является ли число простым, нужно проверить, делится ли оно нацело на какое-либо число, кроме 1 и самого себя. Если оно не делится нацело ни на одно число, кроме 1 и самого себя, то оно является простым.

Какую роль играют простые числа в математике?

Простые числа играют важную роль в математике. Они используются в различных алгоритмах, криптографии и теории чисел. Например, простые числа используются в алгоритмах шифрования, факторизации чисел и генерации случайных чисел.